Similarity theorems

from Wikipedia, the free encyclopedia

The similarity theorems are propositions that set sufficient conditions that two triangles are similar . Many statements about geometry can be proven with the help of the similarity of triangles.

The four similarity theorems for triangles

The four similarity theorems for triangles are:

  • Two triangles are similar to each other if they match at two (and thus three) angles . (W: W: W sentence)
  • Two triangles are similar to each other if they match in all proportions of corresponding sides. (S: S: S phrase)
  • Two triangles are similar to each other if they match at an angle and in the ratio of the adjacent sides. (S: W: S sentence)
  • Two triangles are similar to each other if they match in relation to two sides and in the opposite angle of the larger side. (S: S: W sentence)

See also : Congruence Theorems

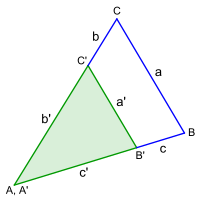
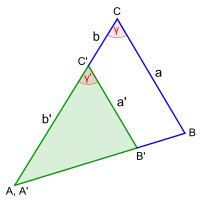
In the following four figures, two similar triangles ABC and A'B'C '- speaking clearly - are "nested".

Then every pair of side lengths in ABC is proportionally equal to the corresponding pair of side lengths in A'B'C '.

  • W: W: W set
    three angles match

  • S: S: S-sentence
    a: a '= (b + b'): b '= (c + c'): c '

  • S: W: S sentence
    a: a '= (b + b'): b ',
    the included angles (γ, γ') match

  • S: S: W sentence
    a: a '= (b + b'): b ',
    the angles (β, β') opposite the larger sides match

literature