Bayesian statistics

This item has been on the quality assurance side of the portal mathematics entered. This is done in order to bring the quality of the mathematics articles to an acceptable level .

Please help fix the shortcomings in this article and please join the discussion ! ( Enter article )

The Bayesian statistics , and Bayesian statistics , Bayesian inference or Bayesian statistics is a branch of statistics that the Bayesian concept of probability and Bayes' Theorem questions of stochastics investigated. The focus on these two pillars establishes Bayesian statistics as a separate “style”. Classical and Bayesian statistics partly lead to the same results, but are not completely equivalent. A characteristic of Bayesian statistics is the consistent use of probability distributions or marginal distributions , the form of which transports the accuracy of the method or the reliability of the data and the method.

The Bayesian concept of probability does not require random experiments that can be repeated infinitely often, so that Bayesian methods can also be used with small data bases. A small amount of data leads to a broad probability distribution that is not strongly localized.

Due to the strict consideration of probability distributions, Bayesian methods are often computationally complex. This is considered to be one reason why frequentist and ad-hoc methods prevailed as formative techniques over Bayesian in statistics in the 20th century . However, with the spread of computers and Monte Carlo sampling methods , complicated Bayesian methods have become possible.

In Bayesian statistics, the conception of probabilities as a “degree of reasonable credibility” opens up a different view of reasoning with statistics (compared to the frequentistic approach of probabilities as the results of infinitely repeatable random experiments). In Bayes' theorem, an existing finding about the variable to be examined (the a priori distribution, or prior for short) is combined with the new findings from the data (“likelihood”, occasionally also “plausibility”), resulting in a new, improved finding ( A posteriori probability distribution) results. The posterior probability distribution is useful as a new prior when new data is available.

Structure of Bayesian procedures

The use of Bayes' theorem leads to a characteristic structure of Bayesian methods. A model is to be examined with a data set . The initial question is how the probabilities for the model parameters are distributed, provided that the data and prior knowledge are given. So we want to find an expression for . ${\ displaystyle {\ mathcal {M}}}$ ${\ displaystyle {\ mathcal {D}}}$ ${\ displaystyle {\ mathcal {M}}}$ ${\ displaystyle {\ mathcal {D}}}$ ${\ displaystyle {\ mathcal {I}}}$ ${\ displaystyle \ Pr ({\ mathcal {M}} \ mid {\ mathcal {D}}, {\ mathcal {I}})}$

{\ displaystyle \ Pr ({\ mathcal {M}} \ mid {\ mathcal {D}}, {\ mathcal {I}}) = {\ frac {\ Pr ({\ mathcal {D}} \ mid {\ mathcal {M}}, {\ mathcal {I}}) \ Pr ({\ mathcal {M}} \ mid {\ mathcal {I}})} {\ Pr ({\ mathcal {D}} \ mid {\ mathcal {I}})}}}

The individual probabilities have a fixed designation.

${\ displaystyle \ Pr ({\ mathcal {M}} \ mid {\ mathcal {I}})}$ A priori probability , i.e. the probability distribution for given prior knowledge (without including the measurement data from the experiment) ${\ displaystyle {\ mathcal {M}}}$ ${\ displaystyle {\ mathcal {I}}}$ ${\ displaystyle {\ mathcal {D}}}$
${\ displaystyle \ Pr ({\ mathcal {M}} \ mid {\ mathcal {D}}, {\ mathcal {I}})}$ A posteriori probability , the probability distribution given the previous knowledge and the measurement data ${\ displaystyle {\ mathcal {M}}}$ ${\ displaystyle {\ mathcal {I}}}$ ${\ displaystyle {\ mathcal {D}}}$
${\ displaystyle \ Pr ({\ mathcal {D}} \ mid {\ mathcal {M}}, {\ mathcal {I}})}$ Likelihood, also inverse probability or “plausibility”, the probability distribution for the measurement data if the model parameter and the prior knowledge are given. ${\ displaystyle {\ mathcal {D}}}$ ${\ displaystyle {\ mathcal {M}}}$ ${\ displaystyle {\ mathcal {I}}}$
${\ displaystyle \ Pr ({\ mathcal {D}} \ mid {\ mathcal {I}})}$ Evidence, can be determined as a normalization factor.

Bayes' theorem leads directly to an important aspect of Bayesian statistics: With the parameter , prior knowledge about the outcome of the experiment is included in the evaluation as a prior. After the experiment, a posterior distribution is calculated from previous knowledge and measurement data, which contains new findings. The posterior of the first experiment is for the following experiments then used as the new Prior, who has an advanced knowledge, so . ${\ displaystyle {\ mathcal {I}}}$ ${\ displaystyle {\ mathcal {I}} '= \ {{\ mathcal {I}}, {\ mathcal {D}} \}}$

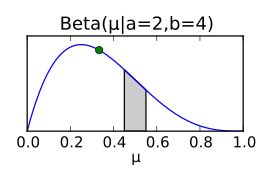
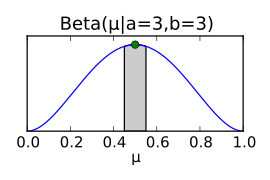
The following figure shows a prior with prior knowledge on the left: is distributed around 0.5, but the distribution is very broad. With binomially distributed measurement data (middle), the distribution is now determined more precisely so that a narrower, more acute distribution than posterior (right) can be derived. For further observations, this posterior can again serve as a prior. If the measurement data correspond to the previous expectations, the breadth of the probability density function can decrease further; in the case of measurement data deviating from previous knowledge, the variance of the distribution would increase again and the expected value would possibly shift. ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$

Bayesian concept of probability

The Bayesian concept of probability defines probabilities as the “degree of reasonable expectation”, ie as a measure of the credibility of a statement that ranges from 0 (false, untrustworthy) to 1 (credible, true). This interpretation of probabilities and statistics differs fundamentally from the observation in conventional statistics, in which random experiments that can be repeated infinitely often are examined from the point of view of whether a hypothesis is true or false.

Bayesian probabilities relate to a statement . In classical logic , statements can either be true (often represented with the value 1) or false (value 0). The Bayesian concept of probability now allows intermediate stages between the extremes, a probability of 0.25, for example, indicates that there is a tendency that the statement could be wrong, but there is no certainty. It is also possible, similar to classical propositional logic, to determine more complex probabilities from elementary probabilities and statements. Bayesian statistics enable conclusions to be drawn and complex questions to be dealt with. ${\ displaystyle P (A)}$ ${\ displaystyle A}$

common probabilities , i.e. how likely is it that both and are true? How likely is it, for example, that my shoes will be dry on a walk and that it will rain at the same time. ${\ displaystyle P (A, B)}$ ${\ displaystyle A}$ ${\ displaystyle B}$

Conditional probabilities , that is: How likely is it that is true when it is given that is true. For example, how likely is it that my shoes will be wet after taking a walk outside if it is currently raining? ${\ displaystyle P (A \ mid B)}$ ${\ displaystyle A}$ ${\ displaystyle B}$

Bayesian inference using the example of the coin toss

The coin toss is a classic example of the calculus of probability and is very suitable for explaining the properties of Bayesian statistics. It is considered whether “heads” (1) or non-heads (0, ie “tails”) occurs when a coin is tossed. Typically, it is often assumed in everyday life that when a coin flip, there is a 50% probability to find a specific page on top to: . However, this assumption does not make sense for a coin that has large bumps or maybe even has been tampered with. The probability of 50% is therefore not taken as given in the following, but replaced by the variable parameter . ${\ displaystyle p (K) = 0 {,} 5}$ ${\ displaystyle \ mu}$

The Bayesian approach can be used to investigate how likely any values are for , i.e. how balanced the coin is. Mathematically, this corresponds to seeking a probability distribution , said observations (number of litters head and number of throws in an experiment with flips) should be considered: . With Bayesian theorem, this probability function can be expressed in terms of likelihood and a priori distribution: ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$ ${\ displaystyle m}$ ${\ displaystyle Nm}$ ${\ displaystyle N}$ ${\ displaystyle \ Pr (\ mu | m, N)}$

{\ displaystyle {\ underset {\ text {Posterior}} {\ underbrace {\ Pr (\ mu \ mid m, N)}}} \ propto {\ underset {\ text {Likelihood}} {\ underbrace {\ Pr ( m \ mid \ mu, N)}}} {\ underset {\ text {Prior}} {\ underbrace {\ Pr (\ mu)}}}}

The likelihood here is a probability distribution over the number of head tosses given a given balance of the coin and a given number of tosses in total . This probability distribution is known as the binomial distribution ${\ displaystyle \ mu}$ ${\ displaystyle N}$

{\ displaystyle \ Pr (m \ mid \ mu, N) = \ mathrm {Binom} (m \ mid N, \ mu) = {\ binom {N} {m}} \ mu ^ {m} (1- \ mu) ^ {Nm}}

.

In contrast to the posterior distribution, there is only one parameter in the likelihood distribution that determines the shape of the distribution. ${\ displaystyle \ mu}$

To determine the a posteriori distribution, the a priori distribution is now missing . Here too - as with the likelihood - a suitable distribution function for the problem must be found. In a binomial distribution as a likelihood a suitable Beta distribution as a priori distribution (due to the binomial Terme ). ${\ displaystyle \ mu ^ {\ alpha -1} (1- \ mu) ^ {\ beta -1}}$

{\ displaystyle \ Pr (\ mu) = \ mathrm {Beta} (\ mu \ mid \ alpha, \ beta) = {\ frac {1} {B (\ alpha, \ beta)}} \ mu ^ {\ alpha -1} (1- \ mu) ^ {\ beta -1}}

.

The parameters of the beta distribution will be clearly understandable at the end of the derivation of the posterior. Combining the product of the likelihood distribution and beta prior together yields a (new) beta distribution as posterior. ${\ displaystyle \ alpha, \ beta}$

{\ displaystyle \ Pr (\ mu \ mid m, N, \ alpha, \ beta) = \ mathrm {Beta} (\ mu \ mid \ alpha + m, \ beta + (Nm))}

It follows from Bayesian approach that the a posteriori distribution of the parameter can be expressed as a beta distribution, the parameters of which are obtained directly from the parameters of the a priori distribution and the measurement data obtained (number of head throws) leaves. This a posteriori distribution can again be used as a prior for an update of the probability distribution if, for example, more data is available through further coin flips. In the following figure, the posterior distributions for simulated coin toss data are plotted for each coin toss. The graphic shows how the posterior distribution approaches the simulation parameter µ = 0.35 (represented by the green point) with increasing number of throws. The behavior of the expected value of the posterior distribution (blue point) is particularly interesting here, since the expected value of the beta distribution does not necessarily correspond to the highest point of the beta distribution. ${\ displaystyle \ mu}$

The probability distribution over allows - in the Bayesian sense - not only to indicate the most likely value for but also to indicate the accuracy of given the data. ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$

Choice of prior

The choice of a priori distribution is by no means arbitrary. In the above case, an a priori distribution - the conjugate prior - was chosen, which is mathematically practical. The distribution is a distribution where everyone is equally likely. This beta distribution therefore corresponds to the case that there is no noteworthy prior knowledge about . After a few observations, the uniform prior can become a probability distribution that describes the position of much more precisely, for example . ${\ displaystyle \ mathrm {Beta} (\ mu \ mid \ alpha = 1, \ beta = 1)}$ ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$ ${\ displaystyle \ mu}$ ${\ displaystyle \ mathrm {Beta} (\ mu \ mid \ alpha = 11, \ beta = 12)}$

The prior can also contain “expert knowledge”. In the case of a coin, for example, it can be assumed that it is close to 50%, while values in the marginal areas (around 100% and 0%) are unlikely. With this knowledge, the choice of a prior with the expected value 0.5 can be justified. This choice might not be appropriate in another case, such as the distribution of red and black balls in an urn, for example if it is not known what the mixing ratio is or whether both colors are in the urn at all. ${\ displaystyle \ mu}$

The Jeffreys' prior is what is known as a non-informational prior (or rather a method of determining a non-informational prior). The basic idea for the Jeffreys Prior is that a procedure for prior selection, which takes place without prior knowledge of data, should not depend on the parameterization. Jeffreys is prior to a Bernoulli trial . ${\ displaystyle \ mathrm {Beta} (\ mu \ mid \ alpha = {\ tfrac {1} {2}}, \ beta = {\ tfrac {1} {2}})}$

Other prior distributions are also conceivable and can be used. In some cases, however, the determination of the posterior distribution becomes difficult and it can often only be mastered numerically.

Conjugated priors exist for all members of the exponential family .

Differences and similarities to non-Bayesian methods

Most non-Bayesian methods differ from Bayesian methods in two ways. On the one hand, non-Bayesian methods do not give Bayes' theorem of central importance (they often do not use it); on the other hand, they are often based on another concept of probability: the frequentist concept of probability . In the frequentistic interpretation of probabilities, probabilities are frequency ratios that can be repeated infinitely often.

Depending on the method used, no probability distribution is determined, but only expected values and, if necessary, confidence intervals. However, these restrictions often lead to numerically simple calculation methods in frequentistic or ad hoc methods. In order to validate their results, non-Bayesian methods provide extensive techniques for validation.

Maximum likelihood approach

The maximum likelihood approach is a non-Bayesian standard statistical method. In contrast to Bayesian statistics, Bayes' theorem is not used to determine a posterior distribution of the model parameter, but rather the model parameter is varied in such a way that the likelihood function is maximal.

Since only the observed events are random variables in the frequentistic picture , with the maximum likelihood approach the likelihood is not understood as a probability distribution of the data given the model parameters , but as a function . The result of a maximum likelihood estimation is an estimator that is most closely comparable with the expected value of the posterior distribution in the Bayesian approach. ${\ displaystyle {\ mathcal {D}}}$ ${\ displaystyle {\ mathcal {M}}}$ ${\ displaystyle L: {\ mathcal {M}} \ mapsto \ Pr ({\ mathcal {D}} \ mid {\ mathcal {M}})}$ ${\ displaystyle {\ mathcal {M}} _ {ML}}$

The maximum likelihood method does not completely contradict Bayesian statistics. With the Kullback-Leibler divergence it can be shown that maximum likelihood methods approximately estimate model parameters that correspond to the actual distribution.

Examples

Example from Laplace

Accuracy of the estimate of Saturn's mass as a fraction of the solar mass
Bouvard (1814)	3512.0
NASA (2004)	3499.1
Deviation: ${\ displaystyle {\ tfrac {3512 {,} 0-3499 {,} 1} {3499 {,} 1}} = 0 {,} 0037 <0 {,} 01}$

Laplace derived Bayes' theorem again and used it to narrow down the mass of Saturn and other planets .

A: The mass of Saturn lies in a certain interval
B: Data from observatories on mutual interference between Jupiter and Saturn
C: The mass of Saturn cannot be so small that it loses its rings and not so large that it destroys the solar system .

«Pour en donner quelques applications intéressantes, j'ai profité de l'immense travail que M. Bouvard vient de terminer sur les mouvemens de Jupiter et de Saturne, dont il a construit des tables très précises. Il a discuté avec le plus grand soin les oppositions et les quadratures de ces deux planètes, observées par Bradley et par les astronomes qui l'ont suivi jusqu'à ces dernières années; il en a concluu les corrections des élémens de leur mouvement et leurs masses comparées à celle du Soleil, prize pour unité. Ses calculs lui thonnent la masse de Saturne égale à la 3512e partie de celle du Soleil. En leur appliquant mes formules de probabilité, je trouve qu'il ya onze mille à parier contre un, que l'erreur de ce résultat n'est pas un centième de sa valeur, ou, ce qui revient à très peu près au même, qu'après un siècle de nouvelles observations ajoutées aux précédentes, et discutées de la même manière, le nouveau résultat ne différera pas d'un centième de celui de M. Bouvard. »

“To name some interesting applications of it, I have benefited from the tremendous work that M. Bouvard has just finished on the motions of Jupiter and Saturn, and from which he has made very precise tables. He has carefully discussed the oppositions and squarings of these two planets observed by Bradley and the astronomers who have accompanied him over the years; he concluded the corrections of the elements of their motion and their masses compared to the sun, which was used as a reference. According to his calculations, the mass of Saturn is 3512th of the solar mass. Applying my formulas of probability calculus to this, I come to the conclusion that the odds are 11,000 to 1, that the error of this result is not a hundredth of its value, or, which means the same, that even after a century of new observations , in addition to the existing ones, the new result will not differ by more than a hundredth from that of M. Bouvard, provided they are carried out in the same way. "

- Pierre-Simon Laplace : Essai philosophique sur les probabilités. Dover 1840, pp. 91-134

The deviation from the correct value was actually only about 0.37 percent, i.e. significantly less than a hundredth.

literature

Christopher M. Bishop: Pattern Recognition And Machine Learning . 2nd Edition. Springer, New York 2006, ISBN 0-387-31073-8 .
Leonhard Held: Methods of statistical inference. Likelihood and Bayes . Spectrum Akademischer Verlag, Heidelberg 2008, ISBN 978-3-8274-1939-2 .
Rudolf Koch: Introduction to Bayesian Statistics . Springer, Berlin / Heidelberg 2000, ISBN 3-540-66670-2 .
Peter M. Lee: Bayesian Statistics. An Introduction . 4th edition. Wiley, New York 2012, ISBN 978-1-118-33257-3 .
David JC MacKay: Information Theory, Inference and Learning Algorithms. Cambridge University Press, Cambridge 2003, ISBN 0-521-64298-1 .
Dieter Wickmann: Bayes Statistics. Gain insight and decide in the event of uncertainty (= Mathematical Texts Volume 4 ). Bibliographisches Institut Wissenschaftsverlag, Mannheim / Vienna / Zurich 1991, ISBN 3-411-14671-0 .

Individual evidence

↑ Christopher M. Bishop: Pattern Recognition And Machine Learning. 2nd Edition. Springer, New York 2006, ISBN 978-0-387-31073-2 .
^ RT Cox: "Probability, Frequency and Reasonable Expectation", Am. J. Phys. 14, 1 (1946); doi: 10.1119 / 1.1990764 .
^ Pierre-Simon Laplace: Essai philosophique sur les probabilités. Dover 1840, pages 91-134, digital full-text edition at Wikisource (French).

[1] Christopher M. Bishop: Pattern Recognition And Machine Learning. 2nd Edition. Springer, New York 2006, ISBN 978-0-387-31073-2 .

[2] RT Cox: "Probability, Frequency and Reasonable Expectation", Am. J. Phys. 14, 1 (1946); doi: 10.1119 / 1.1990764 .

[3] Pierre-Simon Laplace: Essai philosophique sur les probabilités. Dover 1840, pages 91-134, digital full-text edition at Wikisource (French).