Deconvolution

With deconvolution ( German development ) is called the inverse of the so-called. Convolution operation . This is a mathematical transformation that is used in signal and image processing , among other things . A convolution can always be computed, while its inversion is not always possible because information can be lost during the convolution that cannot be restored. In order to still be able to calculate the best possible inverse convolution, computationally intensive algorithms and methods were developed.

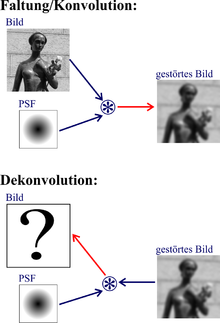
A simple example is sharpening an image. The process of blurring (blurring) is represented by a convolution. The sharpening of the image, as supported by many image processing programs, then corresponds to a deconvolution (see picture on the right).

mathematics

In mathematics, deconvolution or unfolding describes the reversal of a convolution (symbolically: " " to avoid confusion with point-by-point multiplication, see below) of two functions. In general terms, this corresponds to the attempt to convert two functions g and h from the result f ${\ textstyle *}$

{\ displaystyle f = g * h \,}

determine the unknown function g with known h and f ; this problem is also known as the inverse convolution problem . A general approach to a solution results from the convolution theorem , which states that the Fourier transform of a convolution of two functions is equal to the product of the Fourier transform of the two functions. Accordingly, the above equation can also be written as

{\ displaystyle {\ hat {f}} = {\ hat {g}} \ cdot {\ hat {h}}}

where , and denote the Fourier transforms of f , g and h . It could thus be determined in principle as ${\ displaystyle {\ hat {f}}}$ ${\ displaystyle {\ hat {g}}}$ ${\ displaystyle {\ hat {h}}}$ ${\ displaystyle {\ hat {g}}}$

{\ displaystyle {\ hat {g}} = {\ frac {\ hat {f}} {\ hat {h}}}}

and from this by inverse Fourier transformation g . However, this general approach is usually not applicable, because firstly the function g does not have to be unique, secondly the function can contain zeros and thirdly, real data is usually subject to additive noise, corresponding to an additional term n , so that in such Cases the original problem too ${\ displaystyle {\ hat {h}}}$

{\ displaystyle f = g * h + n \,}

complicated. For this reason, various methods are used that try to determine the most probable result for g from h and f , since an unambiguous analytical solution does not exist. It turns out that the noise n is increased disproportionately with a naive aliasing with the above division method:

{\ displaystyle {\ hat {g}} = {\ frac {\ hat {f}} {\ hat {h}}} - {\ frac {\ hat {n}} {\ hat {h}}}}

The amplification is due to the fact that at high frequencies it usually drops towards 0 (e.g. smoothing filter = low-pass filter), while the noise also contains frequency components there, which are then amplified by. ${\ displaystyle {\ hat {h}}}$ ${\ displaystyle 1 / {\ hat {h}}}$

Image processing

Deconvolution is used, for example, to sharpen images in astrophotography and microscopy. Deconvolution filters try to mathematically capture the blurring and reverse it. Some procedures are:

Van Cittert deconvolution
Viennese deconvolution
Richardson-Lucy Deconvolution
blind deconvolution or German blind development
Meinel deconvolution
ZNova algorithm or ZNova deconvolution
Agard-Sedat deconvolution

The sharpening takes place via the so-called PSF matrix (engl .: point spread function , the point spread ). This describes the process that created the blurring. It can e.g. B. the filter mask of a fuzzy filter (e.g. binomial filter ). A PSF can also be calculated for any optical imaging system, such as the objective of a camera or a microscope (for example with the PSF Lab software for a confocal microscope ). A complete restoration of an image is often not possible because information is lost when it is "blurred". The procedures listed here try to recover as much information as possible from the PSF and the image. “ Blind deconvolution ” tries to estimate the optimal PSF matrix from the image.

Individual evidence

↑ Michael J. Nasse, Jörg C. Woehl: Realistic modeling of the illumination point spread function in confocal scanning optical microscopy. In: The Journal of the Optical Society of America A. Vol. 27, No. 2, 2010, ISSN 1084-7529 , pp. 295-302, doi : 10.1364 / JOSAA.27.000295 .

Web links

Tim Cornwell, Alan Bridle: Deconvolution Tutorial . National Radio Astronomy Observatory, Nov. 4, 2006.

[1] Michael J. Nasse, Jörg C. Woehl: Realistic modeling of the illumination point spread function in confocal scanning optical microscopy. In: The Journal of the Optical Society of America A. Vol. 27, No. 2, 2010, ISSN 1084-7529 , pp. 295-302, doi : 10.1364 / JOSAA.27.000295 .