IS function
The IS function , also called the IS equation or IS curve , is an economic model of macroeconomics . It represents the amount of all combinations of interest rate and national income for which there is an equilibrium in the goods market . Together with the LM function , she constructs the IS-LM model , which is the most important interpretation of Keynesian theory .
The IS equation is one of the most important macroeconomic analysis tools. It is required for the construction of the Keynes model and the Mundell-Fleming model.
In a closed economy , this means that investments (I) are equal to savings (S), whereas in an open economy the expression equates income or production (Y) to demand for goods (Z).
Basics
Because Y = C + S and Y = C + I we get the identity equation S = I, so the economic saving is always identical to the net investment . Saving and investment is a tautology because the capital stock of an economy grows around the net investment and it is precisely this growth in the capital stock that represents the saving. The net investment is identical to the saving of the economy.
A balance on the goods market , we obtained under the condition that the planned savings coincides with the planned investment. It can therefore be that the investment resulted in higher or lower savings than planned, or that the demand for goods resulted in an unplanned build-up or reduction of inventory and thus unwanted investment or disinvestment. The always identical investments and savings in a period of time can contain unplanned and undesired components, so that the goods market is not in equilibrium because the investors and savers will then change their dispositions accordingly.
It can never be objectively determined whether the goods market is actually in equilibrium and whether the planned investment corresponds exactly to the voluntary savings. One can only assert with assumptions about the interest rate dependency of the planned investment and the income dependency of voluntary saving that with a certain combination of interest and income an equilibrium of the goods market would exist.
Application examples
Like every model, the Keynes model and the Mundell-Fleming model represent a simplification of reality. With their help, economic relationships and processes can be represented. The IS function is used to explain the interrelationships of the factors in the goods market. They are mainly found in connection with the effects of political decisions as well as changes in income and interest rates on the goods market, e.g. B. How the IS-LM model changes due to the lowering of taxes.
Mathematical derivation
First, the derivation of the IS function is presented in a closed economy in which there is no foreign trade. So it is assumed that there are neither exports nor imports.
As already mentioned above, the equilibrium on the goods market in a closed economy with a balanced state budget is represented by equating investment and private saving :
With
- I = investment
- i = interest rate
- S = save
- Y = income
Investment curve
To include the relationship between the interest rate and investment in the model, the dependency I = I (i) is used (Figure 1). The investment function is represented as follows:
With
- = autonomous investment
- b = interest rate sensitivity
The variable \ overline I is the investment, which is independent of income and interest rate.
The variable b is the measure of how strongly the investments react to the interest rate level . The function can show the planned investment amount for each interest rate level. If you transform this formula according to i , you get the function:
- It should be noted here that b and are constants, i.e. fixed values.
It corresponds to the graphic representation in Figure 1.
A high variable b , meaning a strong reaction of the investments to the interest rate changes, leads to a flat curve display. Even small changes in interest rates lead to major changes in the investment volume on a flat curve. The slope of the straight line is -1 / b . It describes an inverse relationship between investment and interest. A rise in interest rates leads to a decrease in investment. Because the interest rate represents the cost of investment financing, an increase in the interest rate leads to a decrease in investment. It can also be deduced from this that there is a negative relationship between the interest rate and income level in the goods market, i.e. that is, the total equilibrium income decreases as the interest rate increases .
If the bank were to raise the interest on its loans, it would have various effects.
- Investments (I) decrease because the capital stock is not increased by taking out new loans, i. H. fewer loans are taken out.
- When the investment is reduced, the total expenditure is reduced. This leads to a lower level of income.
In the event of a reduction in the interest rate, the opposite effect would be observed.
Savings volume
The savings volume is defined as:
With
- = disposable income
- = Consumer spending by private households
With
- T = taxes
In this formula z. B. the social security and the transfer payments consolidated to "0", d. i.e., they are ignored. A practical example is the decision of the state to increase taxes. The effect of this increase is that the household has less income and can consume less.
The savings volume can thus be used as the function:
being represented. After changing the formula, the amount of savings depends not only on taxes, but also on consumer spending by private households.
Equilibrium in the goods market
In order to arrive at the IS function, the equilibrium on the goods market is shown:
With
- Y = production
- Z = demand for goods
Aggregate demand can be described as the sum of investment, government spending and consumer demand:
With
- G = government expenditure
In a closed economy, the external contribution can be neglected.
So it results:
Derivation of the IS function
By transforming (| -T | -C) one obtains the function:
At the previous point the term YTC was already defined as S and after reshaping it receives (| + T | -G):
The individual variables can be defined as follows:
- S = private saving
- (TG) = state saving
When the state budget is balanced, the equation can be simplified as shown.
Macroeconomic interrelationships of the IS function
It must also be noted that consumption and the decision to save are related. Once the household has determined its consumption plan with its given disposable income, the budget constraints also determine the savings. Just as the consumption behavior is specified, the following results for the saving behavior:
With
- = autonomous consumption rate
- = marginal consumption rate
Forming gives:
The variable indicates how much of the disposable income or is consumed. The variable can be interpreted as a propensity to consume, so the opposite expression can be referred to as a propensity to save. It indicates how much a consumer is willing to save from an additional unit of income. Because the propensity to consume is assumed, the propensity to save is between zero and one. Furthermore, it can be said that personal savings (YT) can only increase by.
If the above expression is now inserted in the IS function for private savings, the result is:
or broken down by income:
This formula can now be used to consider the paradox of savings that Keynes emphasized. If the consumer decides to save more for a given income, i. H. if it is reduced, consumption is reduced and savings increase. The above equation shows that equilibrium income is going down. The lower consumer demand in turn causes production to fall. Consumers are now saving more at every income level; H. the savings increase. At the same time, income falls, which means savings are reduced. What is the effect of this change? The equilibrium condition of the equation I = S + (TG) makes it clear that the savings cannot change because G and T define the state budget and I remains unchanged. The attempt of the consumer to save more leads to a decrease in production and thus the savings to remain the same. This result is known as the savings paradox.
Graphic derivation
The IS curve comes from macroeconomics and represents all combinations in which investing and saving match, so that an equilibrium arises in the goods market. Together with the LM curve , it is used to represent the Keynesian theory. The LM curve represents the equilibrium on the money market . If the two curves are combined, the result is the IS-LM model. With this model, macroeconomic relationships become clear and the effects of changes in interest rates or government measures such as B: Tax increases, noticeable.
requirements
In order to be able to represent and explain the IS curve, the components of the curve must be defined in advance. The IS curve results from equating investment and saving (I = S). However, this version has to be expanded in order to understand the chain of effects behind it. The investments must be supplemented by the interest rate dependency and the saving by the income dependency. This results in the following more exact representation of the IS curve: I (i) = S (Y). The investments in the model are 100% financed through the market. The money must therefore come from household savings.
In the case of a variable interest rate, a corresponding income can be determined for each interest rate . This ensures that I and S match. In summary, the following chain of effects can be derived from an interest rate hike. The rising interest rates make investments more expensive. This has the consequence that the demand for investments decreases. This in turn triggers a contracting multiplier process and income falls, which in turn has a negative effect on savings behavior. Investments and savings are thus back in balance. These statements lead to the following result:
- Savings benefit is positively dependent on income.
- Investments are negatively dependent on interest, but the amount invested also depends on the expected income.
The IS curve can be explained using two possible ways: on the one hand, using the four-quadrant scheme (from a capital perspective) and, on the other hand, based on the macroeconomic demand curve (from a goods perspective).
Deriving the IS curve from the macroeconomic demand curve
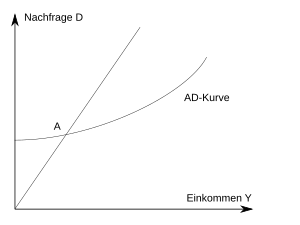
The starting point is the graphical and mathematical representation of the overall economic demand (AD) of a closed economy, with an equilibrium at point A. On the recognizable 45 ° line, the equilibrium condition is fulfilled, i.e. H. AD = Y.
In general, the demand function is composed as follows (based on a closed economy): AD = C + I + G. However, this formula can still be specified. The variable G stands for government spending. The consumption is broken down into C = c 0 + c 1 (YT), with the following meaning of the variables:
- C: consumption
- c 0 : autonomous consumption
- c 1 : marginal consumption rate
- Y: income
- T: Taxes
The investments are broken down into I = Ī-b i , with the variables:
- I: investments made by companies
- Ī: autonomous investments (i.e. independent of interest rates and income)
- b: Measure of how strongly the investments react to the interest rate level (interest rate sensitivity)
- i: interest rate level
The result is the demand function: AD = c 0 + c 1 (YT) + Ī-b i + G
The following graphic shows two AD curves, each for two different interest rate levels (interest rate i '> i). As a result of the rise in interest rates, the demand for investments and thus production decreases for every level of production . This results in a drop in income and a drop in consumption. Because of the multiplier effect , the overall decrease in investment is much larger than the decrease in investment due to the rise in interest rates.
The IS curve is now derived from this shift in the AD curve. For this purpose, the equilibrium point A (with a corresponding income and a given interest rate) is first transferred to the IS diagram. After the interest rate increase just explained, the new interest / income point resulting from it is again transferred to the IS diagram. If both points are connected with each other, the IS curve results.
The four-quadrant scheme
A somewhat more complex and time-consuming derivation option is the four-quadrant scheme, based on this graphic:
The IS curve is determined geometrically in the first quadrant. For this purpose, the investment curve in the second quadrant and the savings curve in the fourth quadrant are used. The third quadrant shows the equilibrium condition I = S, which is always fulfilled on the bisector. The saving function is made up of saving and income, whereby saving is positively dependent on income. The more of the disposable income (after deduction of taxes and consumption ) is still available, the more is saved (S = YTC). The investment function consists of interest and investments. The higher the interest, the less is invested. These functions can be used to summarize the IS curve and the associated chain of effects. If interest rates rise, the demand for investments falls. The resulting decline in production also reduces income and savings. Thus the equation of the IS curve is fulfilled again (I (i) = S (Y)).
pitch
The IS curve has a negative slope , since with an increase in the interest rate (+) the income decreases (-): Companies ask for less capital, thus produce fewer goods and therefore pay households less income.
Since the interest rate is usually viewed as unaffected, the value of the slope and thus the level of income depends on the interest rate elasticity of investment demand . This value indicates how much a percentage change in the interest rate affects the demand for capital goods .
The more elastic (stronger) the demand for capital goods reacts to changes in interest rates, the flatter the curve runs up to the horizontal with perfect elasticity. The other extreme is a completely inelastic elasticity that leads to a perpendicular IS curve.
Shift of the IS curve
Based on the overall economic demand, a possible shift in the IS curve can be clearly illustrated. So far, the IS curve has been shown for given taxes T and given government expenditure G. Interest-related changes were only reflected in the curve. If one of these non-interest-related demand variables is changed, this leads to a shift.
The following graphic illustrates this process:
The starting point is the IS curve for a given T and G.
The shift in the event of a tax increase from T to T 'is examined. As a result, income and consumption decrease (given the interest rate). There is a decrease in the demand for goods and thus also a decrease in equilibrium income. This graphically shifts the IS curve to the left.
A decline in government spending or a loss of consumer confidence would lead to the same result.
The opposite effect arises from tax cuts, an increase in government spending or an increase in consumer confidence. With all three factors equilibrium income would increase and the IS curve would shift to the right as a result (given the interest rate).
Effect of monetary and fiscal policy on the IS function
The following table is intended to illustrate the relationship to the practice of fiscal policy in a government.
| Measures / event | Variable flow | IS function effect |
IS curves change |
|
|---|---|---|---|---|
| Fiscal policy | Tax increase | T increases | I and Y decrease 2 | To the left |
| Tax cut | T goes down | I and Y increase 1 | To the right | |
| Increase in government spending | G increases | I and Y increase 1 | To the right | |
| Decline in government spending | G goes down | I and Y decrease 2 | To the left | |
| Monetary policy | Increase in money supply | No influence on IS variables | No influence | No influence |
| Decline in money supply | No influence on IS variables | No influence | No influence | |
An increase in government spending or a tax cut increases demand at any level of the interest rate. There is an excess demand for goods. As “Y” increases, the interest rate rises, as income expansion increases demand for money.
Reflects the opposite effect.
IS function in an open economy
If trade relations with the rest of the world are ignored, there is no need to distinguish between domestic demand for goods and demand for domestic goods. In practice, however, part of the domestic demand for foreign goods and part of the demand for domestic goods comes from abroad. The modified demand function for domestic goods thus results:
With
- X = demand for domestic goods
- = Price of domestic goods in units of foreign goods
The terms C , I , G were defined in the Mathematical Derivation section . In a closed economy, they reflect the domestic demand for goods and at the same time the demand for domestic goods. Now two more terms have been added: X and IM (e) . The variable X stands for the demand for domestic goods. It is influenced among other things by the production of the rest of the world. The increase in foreign production leads to an increase in the domestic demand for all goods. A part of the additional demand is accounted for by domestic goods, which means that exports are increasing.
The variable IM stands for the import quantity, i. H. it describes the demand for foreign goods. IM depends on Y among other things . A high income leads to a higher import.
These two terms X and IM are influenced by the exchange rate (e) . The Mundell-Fleming model is based on rigid prices, which means that changes in the real and nominal exchange rates are proportional to one another. A higher nominal exchange rate makes foreign goods cheaper than domestic goods and thus dampens exports and stimulates imports . The opposite would be true if the nominal exchange rate were lower. In some books, X-IM (e) is also summarized as NX (e) , the net export .
The terms "I", "C" and "G" hardly need to be adjusted or not at all, so the analysis of the variables from the closed economy can be used further. The decisions of consumers continue to depend on income and wealth. The change has only very little effect on the level of consumer spending.
The changes in exchange rates due to interest rates are explained by the Mundell-Fleming model. When the domestic interest rate exceeds the world interest rate (Figure 3A), the exchange rate rises as foreign investors seek to invest wealth domestically. The reverse case can also be possible, i.e. H. the domestic interest rate is below the world rate (Figure 3B) and domestic investors are trying to invest overseas, revising the domestic exchange rate downwards.
Individual evidence
- ↑ Mankiw, 1993, p. 314.
- ↑ Rettig, Voggenreiter, 1996, p. 153 f.
- ↑ a b c d Blanchard, Illing, 2006, p. 98 f.
- ↑ Dornbusch, Fischer, 1993, p. 109 f.
- ↑ Dornbusch, Fischer, 1993, p. 110.
- ↑ Mankiw, 1993, p. 324.
- ↑ Mankiw, 1993, p. 324 ff.
- ↑ a b Blanchard, Illing, 2006, p. 99f.
- ↑ a b c d "www.makroo.de"
- ↑ O. Blanchard, G. Illing: Macroeconomics. 3. Edition. Pearson Study, p. 142.
- ↑ a b O. Blanchard, G. Illing: Macroeconomics. 3rd edition, Pearson Studium, p. 144.
- ↑ uni-freiburg, URL: http://www.vwl.uni-freiburg.de/fakultaet/fiwiII/alte%20seite/makro6.pdf uni-freiburg, The IS and LM model, from April 9, 2008.
- ↑ Dornbusch, Fischer, 1993, p. 155 f.
- ↑ Blanchard, Illing, 2006, p. 543.
- ↑ Olivier Blanchard, Gerhard Illing: Macroeconomics. 4th, updated and exp. Edition. Pearson Studium, Munich 2006, p. 540 ff.
- ↑ a b Blanchard, Illing, 2006, pp. 541f.
- ↑ Mankiw, 1993, p. 237 ff.
- ↑ Mankiw, 1993, p. 457.
literature
- Olivier Blanchard , Gerhard Illing: Macroeconomics. 4th edition. Pearson Studium, Munich 2006, ISBN 3-8273-7209-7 .
- Stanley Dornbusch, Rüdiger Fischer: Macroeconomics. 6th edition. Oldenbourg, Munich 1995, ISBN 3-486-22800-5 .
- N. Gregory Mankiw: Macroeconomics. Gabler, Lengerich / Westphalia 1993, ISBN 0-324-23695-6 .
- Rolf Rettig, Dieter Voggenreiter: Macroeconomic Theory. 6th edition. Werner-Verlag, Düsseldorf 1996, ISBN 3-8041-3059-3 .
- Bernhard Felderer , Stefan Homburg : Macroeconomics and New Macroeconomics. Springer, 2005, ISBN 3-540-25020-4 .
- Egon Görgens, Karlheinz Ruckriegel, Karl W. Giersberg: Basic features of macroeconomic theory. 4th edition. Bayreuth 1992, ISBN 3-925710-46-9 .
Web links
- m @ kro> online: The IS curve , April 10, 2008
- Ralf Wagner: Guide to Economics , April 10, 2008