Loxodrome

The Loxodrome from A to B cuts all meridians at a constant angle ${\displaystyle \eta }$

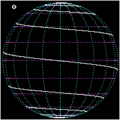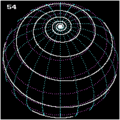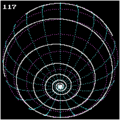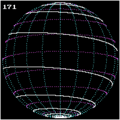
A loxodrome ( gr. Loxos "crooked", dromos "run") is a curve on a spherical surface - e.g. As the earth's surface - that the meridians in the geographic coordinate system always under the same angle cuts and therefore rhumb , angle same or constant curve course is called.

More generally, for every rotation body rhumb lines as curves constant rate. The loxodromes of the sphere are specifically called spherical oxodromes , the loxodromes of a cylinder are helical lines , those of the cone are conical spirals ( conical helices ).

Loxodromes were discovered by Pedro Nunes around 1550 , the name comes from Willebrord Snell (1624).

properties

Except in special cases, intersection angles 0 ° and 90 ° with the meridians, loxodromes are not closed. They spiral around the earth and approach the poles. In the strict sense, a loxodrome reaches the pole after a finite distance, but approaches it asymptotically by winding around it infinitely often. In the vicinity of the pole, a loxodrome has the properties of a (plane) spiral locally , whereas in the vicinity of the equator it has the properties of a helix (spatial spiral).

In the special case of an intersection angle with a meridian of 0 °, the Loxodrome itself is a meridian and thus a great circle that goes through the poles . This is the only case of a loxodrome that reaches the pole. Conversely, this results in the following: Since only the Loxodrome reaches the North Pole at 0 ° , conversely only the Loxodrome starts at 180 ° from the North Pole. From the geographic North Pole, you can only get away in the direction of 180 ° - however, the course information 180 ° at the North Pole is not defined: you could move with this course from the North Pole on any meridian. Only the arrival at the South Pole is guaranteed. In practical navigation, this problem is circumvented by at high latitudes to the grid navigation (Engl. Grid navigation ) working with polar stereographic cards.

In the second special case - angle of intersection 90 ° - the Loxodrome is also closed, it forms a circle of latitude (parallel to latitude), so it is generally not a great circle. The only parallel that is a great circle is the equator , i.e. the loxodrome on which the geographical latitude is constantly 0 °.

Projections:

• In cartography , the loxodromes are shown as straight lines on maps in the Mercator projection . This is what makes the Mercator map useful for practical navigation.
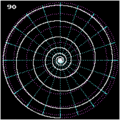
• In a stereographic projection , the curve becomes a logarithmic spiral
• In an orthographic azimuthal projection (parallel plan along the earth's axis), a Poinsot spiral is created

• 

  Animation of a loxodrome

• 

  Loxodrome at the pole

• 

  Loxodrome on the equator

calculation

The formula of the loxodromes (the angle of inclination in the projection) is derived from the aforementioned property of the Mercator projection of depicting loxodromes as straight lines.

• the length is with ${\displaystyle \lambda }$
• the width with designated ${\displaystyle \phi }$

Going west is negative, going east is positive; is positive for latitudes in the northern hemisphere and negative for the southern hemisphere. Both angles are used here mathematically in radians , not degrees ${\displaystyle \lambda }$ ${\displaystyle \phi }$

• the direction angle is a constant bearing in the direction of true north, the slope angle in the Mercator projection, with the slope ${\displaystyle \eta }$ ${\displaystyle k=\cot(\eta )}$

In spatial coordinates

Let be the longitude coordinate of any point on the Loxodrome ( not being restricted to). ${\displaystyle \lambda }$ ${\displaystyle \lambda }$ ${\displaystyle \lbrack 0,\,2\pi \lbrack }$

In the Mercator projection the curve is a straight line :

${\displaystyle x=\lambda ,y=k\lambda }$

For a point of latitude and longitude , the Mercator projection applies due to the mapping rule ${\displaystyle \phi }$ ${\displaystyle \lambda }$

${\displaystyle x=\lambda ,\ y=\operatorname {artanh} (\sin \phi )}$

For the width of the point we get or, expressed as the Gudermann function gd , in Cartesian coordinates , with the radius of a sphere : ${\displaystyle \phi =\arcsin(\tanh(k\lambda ))}$ ${\displaystyle \phi =\operatorname {gd} (k\lambda )}$
${\displaystyle r}$

${\displaystyle {\begin{aligned}x&={\frac {r\cos \lambda }{\cosh(k\lambda )}}&&=r\cos \lambda \cos \left({\frac {1}{\tan(k\lambda )}}\right)\\y&={\frac {r\sin \lambda }{\cosh(k\lambda )}}&&=r\sin \lambda \cos \left({\frac {1}{\tan(k\lambda )}}\right)\\z&=r\tanh(k\lambda )&&=-r\sin \left({\frac {1}{\tan(k\lambda )}}\right)\end{aligned}}}$

In the case of geographical longitude, this curve goes through the equator, for any positions the equatorial passage is , and the expression in the above formulas must be replaced accordingly. ${\displaystyle 0}$ ${\displaystyle \lambda _{0}}$ ${\displaystyle y=k(\lambda -\lambda _{0})}$ ${\displaystyle (k\lambda )}$

In the Mercator projection

Loxodrome (red) and Orthodrome (blue) in Mercator map, with distances in kilometers.

path	Lox.	Orth.	Diff.
NY-MO	8359 km	7511 km	10.1%
NY-DA	6207 km	6150 km	00.9%
DA-MO	6596 km	6509 km	01.3%

In aviation and especially in seafaring, it can be beneficial to travel along a Loxodrome, as you only have to follow one bearing ( compass direction). Although the route of the Loxodrome is always longer than that of the Orthodrome (only if the Loxodrome is on a great circle, they can be the same length), you do not have to constantly calculate a new heading angle . On shorter stretches, navigation on the Loxodrome is only slightly longer than navigation on the Orthodrome. In air traffic, however, Lambert's conformal cone projections are used.

The Mercator projection maps a point with the coordinates on the plane coordinates , where: ${\displaystyle \,(\phi ,\lambda )}$ ${\displaystyle (X,Y)}$

${\displaystyle X=M_{X}(\lambda )=\lambda }$

${\displaystyle Y=M_{Y}(\phi )=\ln \tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)=\operatorname {arcgd} (\phi )}$

with the inverse Gudermann function.

By the Mercator projection of two points and a projection plane is created in the right-angled triangle with a hypotenuse and the right angle at . For the angle at : ${\displaystyle A=(\phi _{A},\lambda _{A})}$ ${\displaystyle B=(\phi _{B},\lambda _{B})}$ ${\displaystyle {\overline {(X_{A},Y_{A}),(X_{B},Y_{B})}}}$ ${\displaystyle (X_{B},Y_{A})}$ ${\displaystyle \,\varphi }$ ${\displaystyle (X_{A},Y_{A})}$

${\displaystyle \tan \varphi ={\frac {Y_{B}-Y_{A}}{X_{B}-X_{A}}}={\frac {M_{Y}(\phi _{B})-M_{Y}(\phi _{A})}{\lambda _{B}-\lambda _{A}}}.}$

Using the two-digit function that supplies the angle of the polar coordinate representation for the Cartesian coordinates and is available as arctan2 or atan2 function in many programming languages, you get: ${\displaystyle \,\varphi (x,y),}$ ${\displaystyle \,(x,y)}$

${\displaystyle \varphi =\varphi {\bigl (}\lambda _{B}-\lambda _{A},\;M_{Y}(\phi _{B})-M_{Y}(\phi _{A}){\bigr )}=\varphi \left(\lambda _{B}-\lambda _{A},\;\ln {\frac {\tan({\frac {\phi _{B}}{2}}+{\frac {\pi }{4}})}{\tan({\frac {\phi _{A}}{2}}+{\frac {\pi }{4}})}}\right).}$

The direction angle of the Loxodrome, which is calculated from north to east in a clockwise direction, is then: ${\displaystyle \,\eta }$

${\displaystyle \eta ={\frac {\pi }{2}}-\varphi }$

The distance you cover - within the Mercator map - between points A and B on the Loxodrome is:

${\displaystyle l={\sqrt {(\phi _{B}-\phi _{A})^{2}+{\Big (}M_{Y}(\phi _{B})-M_{Y}(\phi _{A}){\Big )}^{2}\cdot (\lambda _{B}-\lambda _{A})^{2}}}}$

It should be noted that this is only the shortest loxodrome if it applies, i.e. they are further apart in the west direction than in the east direction, otherwise this is only the second best route. In addition, any number of loxodromes can always be found between any two points (except the poles), which then circle the globe (earth) once or several times. For these cases, another secondary value of the tangent must be selected in the initial equation for . In the Mercator projection, the graph moves beyond the right or left edge and reappears on the other side. ${\displaystyle \lambda _{B}-\lambda _{A}<\pi }$ ${\displaystyle Y=M_{Y}(\phi )}$

Web links

Commons : Loxodrome  - collection of images, videos and audio files

• Escher picture of a loxodrome ( MC Escher , 1958)