Magic number (physics)

The title of this article is ambiguous. Further meanings are listed under Magic number .

In nuclear physics , magic numbers are defined numbers of neutrons and protons in atomic nuclei , in which a higher stability is observed in the basic state of the nucleus than in neighboring nuclides . Such cores themselves are also known as magic cores . The magic numbers can be explained by the shell model of nuclear physics . On this basis, islands of stability are also predicted for ordinal numbers above the naturally occurring elements .

Stability properties

The following observed properties are meant by higher stability:

• Elements with magical numbers of protons are relatively strongly represented in the universe in terms of quantity ( helium , oxygen , calcium , nickel ).
• The binding energy per nucleon is particularly high. This can be seen, for example, in the high energies of alpha and beta decays that lead to magic nuclei.
• The excitation energy of the first excited state of a magical nucleus is particularly high.
• With a magic number of protons there are a particularly large number of stable isotopes ( tin has the most stable isotopes with 10), with a magic number of neutrons there are a particularly large number of stable isotons .
• The cross-section of the nucleus for neutron capture and the energy released during neutron capture are particularly small.
• The quadrupole moment of the nucleus in the ground state has a minimum for magic numbers, which indicates a relatively spherically symmetrical distribution of the electrical charge.

Nuclide map with cross-section for neutron absorption

The magical numbers that can be observed in this way are 2, 8, 20, 28, 50, 82 and 126. However, 126 is only observable for neutrons so far, since nuclides with such a high atomic number (proton number) do not occur in nature and not yet artificially could be produced (see Unbihexium ).

As an example, the picture on the right shows a nuclide map with color coding of the cross-section for neutron capture. The magic numbers of protons and neutrons are highlighted by double lines. It can be seen that this cross-section is usually small in the case of magic atomic nuclei, but far away from magic numbers it is large.

Twice the magic cores

A nuclide is called doubly magic if its proton and neutron number are magical. The stability properties mentioned above are then particularly pronounced. Four doubly magic nuclides are also stable in the absolute sense; H. non- radioactive : helium-4, oxygen-16, calcium-40 and lead-208. Further doubly magic nuclides are calcium-48 (with a half-life of about 6 · 10 ¹⁸  years "almost" absolutely stable), nickel-56, nickel-78, tin-100 and tin-132; Although they are radioactive because of their too large or too small excess of neutrons , they show a relatively increased stability compared to their neighboring nuclides. B. their half-lives.

Explanation by the shell model

Natural elements

The shell model of the atomic nucleus explains the magic numbers by the fact that there (to put it simply) the outermost “shell” is completely occupied, that is, closed , similar to how the chemically stable noble gases are characterized by closed outer shells of their electron shells . Such closures - i.e. a finite maximum number of particles of the same type that can occupy a certain energy level in a potential field - generally occur in quantum mechanics for fermions as a consequence of the Pauli principle .

Artificially created elements

Nuclide map in three-dimensional representation with the expected “island of stability” at 114 protons

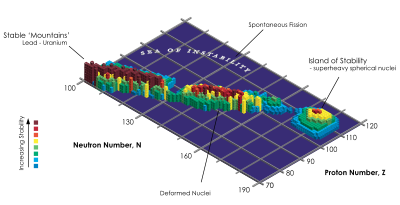
Above the naturally occurring proton and neutron numbers, the theory predicts further shell closures, i.e. magic numbers. For protons, the numbers 114 and 120 result from the subshell closures. In fact, the isotopes of the element Flerovium , which contains 114 protons, that have been discovered so far show remarkably long half-lives (several seconds). The double magic isotope Fl-298 with 184 neutrons, for which a particularly long half-life is to be expected, has not yet been observed. A whole island of stability (a term coined by Glenn Seaborg ) with this doubly magical nuclide as the center is assumed (see illustration). The term stability is only to be understood in relation to the surrounding nuclides; absolutely stable nuclides without any spontaneous decay, i.e. with an infinite half-life, are hardly to be expected beyond lead. Similar "islands" are also expected in the vicinity of the magical ordinal numbers 120 and 126. They would be grouped around the undiscovered doubly magic nuclides unbinilium -304, or unbihexium -310, . ${\displaystyle {}_{120}^{304}\mathrm {Ubn} }$ ${\displaystyle {}_{126}^{310}\mathrm {Ubh} }$

Such nuclides are experimentally produced by fusing heavy nuclei using heavy ion accelerators . The main difficulty in reaching nuclides such as unbinilium is that nuclides with a sufficiently high neutron excess have to be used as target and projectile; these are themselves generally unstable and not available in large quantities.

Explanation by means of group theory

In a paper published in 2010 it is reported that the magic numbers of protons and neutrons also result from considerations based on group theory without assuming a certain form of potential.

Atomic nuclei with a very large excess of neutrons

More recent experimental findings indicate that in nuclei with a particularly large excess of neutrons, besides the magical numbers mentioned above, other numbers occur, the 34 is expected. This indicates that the shell model for such "exotic" nuclei must be refined.

In light, very neutron-rich nuclei, the properties typical of doubly magic nuclides are in some cases more likely to be seen in isotopes with non-magic neutron numbers; For example, they are less pronounced with the double magic oxygen isotope O-28 (proton number Z = 8, neutron number N = 20) than with O-24 ( Z = 8, N = 16). The medium-weight, doubly magic nuclide Ni-78 ( Z = 28, N = 50), on the other hand, shows the typical, expected high excitation energy of the first excited state with 2.6 MeV.

literature

• B. Povh , K. Rith , C. Scholz, F. Zetsche, W. Rodejohann: Particles and nuclei: An introduction to physical concepts. 9th edition, Springer, 2014, ISBN 978-3-642-37821-8

Individual evidence

1. ^ EB Paul: Nuclear and Particle Physics . Amsterdam: North-Holland 1969, pp. 422-423.
2. ^ Richard Herrmann: Higher dimensional mixed fractional rotation groups as a basis for dynamic symmetries generating the spectrum of the deformed Nilsson oscillator . In: Physica A . 389, 2010, p. 693. doi : 10.1016 / j.physa.2009.11.016 .
3. ↑ Jan Oliver Löfken: When are atomic nuclei magical? Pro-Physik, 2005, accessed September 21, 2015.
4. ↑ Holger Dambeck: Nuclear Physics: Researchers discover new magic number. In: Spiegel Online . October 9, 2013, accessed September 21, 2015 . 
5. ↑ CR Hoffman et al., Physics Letters B672 (2009) p. 17
6. ↑ R. Kanungo et al., Physical Review Letters 102 (2009) p. 152501
7. ↑ R. Taniuchi et al., Nature 569 (2019) p. 53