Mereology

The mereology ( Greek. Μέρος meros , Part ') is a section in the ontology and applied logic and deals with the relationship between the part and a whole . Mereology was developed in the context of the debate about the foundation of mathematics . It represents an alternative approach to the set theory that is widely accepted today.

Topological terms such as edge and connection can be examined with mereological means, from which the mereotopology arises. Applications can be found in the field of artificial intelligence in the representation of knowledge .

history

We find a first mereological consideration in Plato's dialog Parmenides , in which Parmenides Socrates deals with the difficulties of defining something as one.

Before the advent of set theory, mathematics and metaphysics were more incidentally thinking about part and whole. So occupied z. B. Edmund Husserl in the second volume of his Logical Investigations from 1901 in detail with the relationship between part and whole - this without formal means. Basic definitions and sentences can already be found there. For example, he has already provided complete proof of transitivity for the partial relationship he is using. Husserl then applied his results to grammatical problems.

A few years earlier, however, formal works on this topic had also been written, which, however, aimed in a different direction: Georg Cantor and later Gottlob Frege developed the first basic features of modern set theory towards the end of the 19th century. The declared aim of this work was not so much the pure preoccupation with part-whole relationships as the search for a system on which the mathematics of the time could be based. This - not yet axiomatized - theory made an important step towards a formal basis for mathematics, but it also raised fundamental problems: Bertrand Russell discovered a contradiction in 1902 when considering the set of all sets that did not contain themselves as elements in this first theory. This contradiction is known today as Russell's antinomy and contributed to the fact that set theory initially met with little recognition. Rather, he made it clear that a system of axioms was necessary for a consistent set theory .

The Polish mathematician Stanisław Leśniewski made a suggestion in this direction that was little noticed at the time . In response to Russell's problem, he developed "a general theory of classes and sets" at the beginning of the 20th century, which he initially called general set theory, but later renamed it "mereology". The aim of his work was an alternative foundation of mathematics to circumvent the aforementioned contradiction. To do this, he refrained from introducing abstract sets that are on a different level than the elements themselves. Instead, he viewed part and whole as "objects of the same ontological category ", namely as concrete objects.

In order to formalize this, he set up his own logical system, which represents a fundamentally different approach than the previously used calculi . In addition to the fact that Leśniewski published his results exclusively in Polish, the lack of awareness of this system contributed to the fact that his theory was initially not well known. Between 1916 and 1931 he published several works on his mereology, but ultimately the axiomatic-set-theoretical ZF system developed in parallel by Ernst Zermelo and Abraham Fraenkel was able to establish itself as the generally recognized basis of mathematics.

Nevertheless, mereological approaches were pursued. In 1940 , the philosophers Henry S. Leonard and Nelson Goodman formulated Leśniewski's approach in classical first-order predicate logic and also researched this topic.

More recently, mereological topics have been increasingly taken up in metaphysics. Well-known authors are Peter Simons, Peter van Inwagen and David Lewis . Some known problems and positions are discussed in more detail in the Metaphysics section .

It is rarely mentioned outside of the specialist literature on metaphysics and artificial intelligence ; the philosopher David Lewis deals with mereology in his 1991 work Parts of classes .

Axiomatization of classical mereological systems

Since Leśniewski's first formal description of a mereology, many other approaches have been taken in similar directions. The British philosopher Peter Simons has identified four basic properties that any theory of true part-whole relationships must meet or demand. Since it is not absolutely necessary for a basic understanding, a more detailed description of the fourth property (“falsehood”) is not given here. The following notations roughly follow Simon's representations in his book “Parts. A Study in Ontology ".

So that a theory about mereology - and more generally about logical considerations - can be clearly noted, it is helpful to define some signs. With the help of these symbols, properties and conditions of the theory can be represented more easily. The symbols for the conjunction ( ), adjunction ( ), the following arrow ( ), the universal quantifier ( ), the existential quantifier ( ), the identity ( ), and the negation ( ) are assumed to be known. ${\displaystyle \land }$ ${\displaystyle \vee }$ ${\displaystyle \longrightarrow }$ ${\displaystyle \forall }$ ${\displaystyle \exists }$ ${\displaystyle \approx }$ ${\displaystyle \lnot }$

First, we define a real partial relationship or relation. With intended to express that a real part of is. The addition "real" excludes that and are identical. This directly implies the first property that Simons calls "asymmetry": ${\displaystyle x\ll y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle \forall x,y(x\ll y\longrightarrow \lnot \left(y\ll x\right))}$

In words, if there is a real part of , then there is not a real part of . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x}$

The second property requires that the relation be transitive, so:

${\displaystyle \forall x,y,z(x\ll y\land y\ll z\longrightarrow x\ll z)}$

In words, if there is a real part of and is a real part of , then there is also a real part of . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle x}$ ${\displaystyle z}$

For the third property, we first define when and overlap. This is obviously the case when and are identical, or when there is a real part of , or when there is a real part of , or when there is one that is a real part of and from . In symbols it results: ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle w}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle x\approx y\vee x\ll y\vee y\ll x\vee \exists w(w\ll x\land w\ll y)}$

We want to designate this property with . With this we can formulate the last requirement, which Simons calls a supplementation: ${\displaystyle x\circ y}$

${\displaystyle \forall x,y(x\ll y\longrightarrow \exists z(z\ll y\land \lnot \left(z\circ x\right)))}$

So next to every real part of there has to be another real part that doesn't overlap with the first. ${\displaystyle x}$ ${\displaystyle y}$

With the help of these symbols, definitions and axioms, mereological considerations can be represented exactly and precisely, so that possible errors and inaccuracies can be discovered quickly. In this way they can help to present complicated theories unambiguously. However, such formal systems also have limits: Unusual new theories in particular often only become understandable when the formulas are expressed in words - as was done here - or illustrated with examples.

metaphysics

In addition to the formal questions about axiomatization and the comparison of different approaches, there are other problems in metaphysics. In this context, the objects in question are compound objects (often also called “complex objects” or “complex substances”). When do objects come together to make something? When are two composite objects identical? And in general, what is composition?

A brief overview of these and other questions will now be given. Since none of these topics has yet been subjected to an exhaustive and universally accepted analysis, only the basic problems and some popular solutions can be presented here, without any claim to correctness or consistency.

The question of the composition

The term “composition” seems clear at first glance: Several (smaller) parts make up a (larger) whole. Such as B. a school class consists of their students or a soccer ball from the individual patches that are sewn together. But as simple as such examples appear, the term becomes complicated on closer analysis. Thus, the German philosopher Johannes Huebner, the question of the composition as follows: "Under what conditions various substances form a complex substance" (Compare with it the previously asked "Special Composition Question" by van Inwagen) Obviously, we already seem an intuitive everyday understanding (in English often called “common sense”) of complex objects. So we usually decide that the students put their class together, but not put together the Reichstag building in Berlin and the Hamburg Elbphilharmonie together but not a complex object. However, the criteria by which we base this distinction no longer seem so easy to name.

In general, there are many different ways to answer this question, three main well-known positions that we will look at in more detail below are the following:

1. The mereological nihilism or atomism.
2. The principle of unrestricted summation (mereological universalism).
3. Moderate mixed positions, accepting complex substances in certain cases and denying them in others.

Mereological Nihilism

The first answer denies the existence of complex substances. No substances form a complex substance under whatever conditions. The obvious discrepancy between this position and our everyday understanding is often resolved as follows: when we speak of a - we mistakenly think - composite object in our everyday language, we actually mean a collection of mereological atoms arranged in the way corresponding to the object . A house is nothing more than mereological atoms arranged like a house.

With a mereological atom is meant an object that has only one part, namely itself. Such objects are therefore regarded mereologically as indivisible and are therefore the only objects that are not put together. This concept obviously does not necessarily coincide with the scientific concept of the atom (because atoms have parts), but also not with that of the currently recognized elementary particles (because these could turn out to be composed in the future). In detail it depends on the mereological and thus the ontological program or claim of the author which objects he describes as mereologically indivisible. So it is e.g. B. also possible to view the level of the physical atoms as the lowest level in order to concentrate his investigations on the higher levels.

In this way, our everyday expressions are reinterpreted as abbreviations and the use of compound objects is avoided.

Principle of unrestricted summation

In a certain way, the second answer represents the exact opposite position to the first: Any object under any conditions forms exactly one complex substance. This view, too, contradicts our everyday understanding, as it allows objects like the one above, which is composed of the Reichstag building and the Elbphilharmonie. So many - intuitively unnecessary - existential assumptions are made, which is why this position is often accused of being “ontologically wasteful”.

The following argument is often used against this accusation: We do not have a name for the above-mentioned unusual object and we do not pay attention to it in our everyday life, but this is not an argument against the fact that the object does not still exist. To clarify this argument, Huebner explains an analogy originally from David Lewis:

"In view of a cleared room [we] hold the statement 'The room is completely empty, not a single object is in it' to be true [...] and [do not] complain that there is a lot of nitrogen and oxygen."

- Johannes Huebner

So we temporarily hide the nitrogen and oxygen atoms because they do not seem relevant to us in the given situation. Yet nobody would say that the atoms are not there just because we are not talking about them. Analogously, we usually do not talk about unusual objects made up of two spatially separate components, but we cannot deduce from this that they do not even exist.

In addition to this first objection, there is another popular argument for the principle of unrestricted summation: David Lewis's thesis of the ontological innocence of mereology. In short, the innocence thesis says that the principle of unrestricted summation does not imply any further ontological obligations. The basis of this argument is the idea that composition is equated with identity. The composite object, which consists of the objects and , is therefore identical with and together - without any other relation or relationship between the objects. If the existence of is assumed and the existence of is assumed, the existence of and together must also be assumed. The composite object thus exists of and , but no further ontological assumption of existence is made than the existence of itself and of itself - and there is no question that these two objects exist. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$

On the one hand, this argument is very simple, but it leads to a result that runs counter to our intuition. We assume the existence of a seemingly new object without increasing the total number of objects in the scenario. This curiosity results from the thesis that composition is nothing other than identity. This assumption is quite controversial and, for this reason, is represented in various forms of weakening. Whether one of these forms can ultimately convince is questionable and the subject of current debate. Hübner criticizes the innocence thesis and comes to the conclusion that it is not justifiable. Other authors, such as David Lewis or David Armstrong, argue for the ontological innocence of mereology.

Mixed positions

The two answers presented so far represent extreme forms. Our everyday understanding is somewhere in between: Some objects put something together, others don't. Some philosophers have also positioned themselves between nihilism and unrestricted summation. Two such positions will now be briefly presented.

The American philosopher Peter van Inwagen has dealt extensively with mereology and formulated the well-known “Special Composition Question”. Similar to Hübner - but a few decades before him - he asks about the conditions that determine which objects form complex objects and which do not. But unlike Hübner (as we will see in a moment) van Inwagen answers the question very simply and clearly: Several things put together a complex object precisely when the activities of these things “constitute a life”. Thus, only living organisms are complex substances, all other objects that we typically assume to exist in everyday life, e.g. B. stones and cars are not put together. Like the question, this position has become very well known, but has also been criticized, changed and rejected over time.

Hübner poses his question about the composition in the tradition of van Inwagen, but relativizes it in order to allow a more differentiated answer. Hübner divides complex material objects into four different types: masses , bodies , artifacts and living beings or organisms. So he does not have to find a general solution, but can give four different answers for the four types. Concerning. The latter type of objects he largely shares with van Inwagen's position; he treats the other sub-questions separately and comes to differentiated results of his own.

These two positions are just a glimpse of the current debate on the subject. Various other questions and answers are conceivable and have already been presented and discussed in detail. New findings from physics , especially quantum mechanics , are constantly providing new problems and approaches in this area. So a generally accepted theory does not seem within reach.

An example

Example on the question of composition

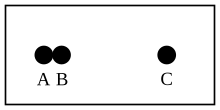
To illustrate the above positions in a small example, please refer to the picture on the right. In this scenario the three mereological atoms exist , and . Otherwise the considered room is empty. Furthermore, the objects and are related in such a way that a force acting on one of the objects always moves the other. The question now is: How many objects exist in this room? The first position, nihilism, accepts the existence of the three mereological atoms and otherwise makes no further assumptions about existence. The fact that and are connected is irrelevant for this position, so there are three objects in space. According to our intuition, we would probably add the object that consists of and (let's call it ) as another object, since the two mereological atoms are connected to one another. That would make four objects. Proponents of the principle of unrestricted summation also assume the existence of the three atoms. In addition, they also postulate the existence of all possible combinations, i.e. the sum of and , as well as the sum of and , as well as the sum of and , and finally the sum of and and . So there would be a total of seven objects. But now there is also the object : Is the sum of and identical to the object ? According to the unrestricted summation, the sum exists anyway and could in principle also be spatially dispersed (as with and, for example). The object, on the other hand, only exists because the two individual objects are connected to one another; if they were separate we would not even consider the existence of . Thus one could argue that the sum of and and the object are different and that there are therefore eight objects in total. The answer to the question seems to be anything but clear - and thus illustrates the differences and problems of the individual positions presented. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle AB}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle AB}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle AB}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle AB}$ ${\displaystyle AB}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle AB}$

Composition and Identity

The question of identity in connection with composition was already addressed in the previous section in connection with the thesis of the ontological innocence of mereology. A well-known example on this subject is the Theseus paradox, also called Theseus' ship , which was first described by Plutarch in antiquity . The basic problem can be summarized as follows:

A seafarer begins a journey with his ship (the Theseus), which is made of wooden planks. Over time, the planks become rotten and have to be replaced by the seaman little by little. In the course of the voyage, all planks are replaced so that at the end of the voyage there is no longer any component of the original ship. The crucial question now is whether the ship with which the voyage started and the ship with which it ended are identical.

If the question is answered in the affirmative, it could be countered that the two ships consist of completely different parts and therefore cannot be identical. On the other hand, if the ships are viewed as different, the question remains as to when the first ship ceased to exist. Already when the first plank was replaced or only later? At first glance, the problem does not seem clearly solvable.

The British philosopher Thomas Hobbes provided an extension of the paradox . He asked what would happen if the original planks of the ship - after they were replaced by new ones - were put together parallel to a new ship. Then the question arises as to which of the two new ships should bear the name Ship of Theseus. There are four basic possible answers to this:

1. The ship made of the new planks is Theseus's ship.
2. The ship made from the original planks is Theseus's ship.
3. Both ships are the ship of Theseus.
4. Neither ship is Theseus's ship.

From a mereological point of view, this leads to the interesting question of when two assembled objects are identical: "One is usually inclined to distinguish a gold ring from the amount of gold that makes it up". If you melt the ring, the resulting lump of gold, like the original ring, is composed of the same parts. To be composed of the same parts does not seem to be a sufficiently strong requirement for identity. On the other hand, in the extended story of Theseus' ship, there are two ships made of completely different wooden planks. Nevertheless, it cannot be dismissed immediately that both ships rightly bear the name Ship of Theseus - and are therefore identical. In this example, the requirement for identical parts is already too strong.

One possible way out of this dilemma, which is often taken in today's research, is so-called four-dimensionalism. Roughly summarized in this theory, every spatial object in our (three-dimensional) world is given a fourth dimension, namely a temporal one. From a four-dimensional perspective, a car at that point in time is by no means identical to the same car at a later point in time . This is completely independent of whether parts of the car have been replaced or removed in the meantime. Just because the car has changed in its fourth dimension (da ), the two objects cannot be identical. ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle t_{1}\neq t_{2}}$

Another reading of four-dimensionalism regards the car at the point in time and the car at the point in time as different time slices of a higher-level object. It becomes clear that the two time slices (i.e. the cars) are themselves three-dimensional objects and are only connected to one another by a four-dimensional object. With the help of this theory, the requirement for identical parts initially seems to be sufficiently strong. ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$

In relation to the gold ring, this means that the lump and the ring cannot be identical, as they exist at different times and thus consist of different parts. For the extended paradox of Theseus, this consideration can also be used to formulate a proposed solution: We name the original ship of Theseus at the beginning of the voyage (time ) . Now one assumes "from the beginning two ships, the first part of which is temporal ". The one ship ( ) is manifested at all later times in the scenario by the ship from which planks are removed. The other ship ( ), on the other hand, only exists again at the end of the voyage (point in time ) as the object that is put together from the old planks. Since both ships are part of and are part of , both ships can rightly be referred to as the ship of Theseus. ${\displaystyle t_{0}}$ ${\displaystyle S_{0}}$ ${\displaystyle S_{0}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle t_{1}}$ ${\displaystyle S_{0}}$ ${\displaystyle A}$ ${\displaystyle B}$

Now, four-dimensionalism is not without controversy in the discussed debate. In the specific case of the ship of Theseus, z. B. stated that if the ship is destroyed shortly after the start of the voyage, no further (four-dimensional) parts of the two ships A and B exist anymore. Thus consist both of and exclusively of . Have so and but exactly the same parts and therefore would have to be identical. However, this contradicts the first assumption that two ships already exist at the time . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle S_{0}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle t_{0}}$

In general, however, it can also be argued against this proposed solution that a simple and almost everyday problem can only be solved in a very complex way and with the help of a comprehensive theory. In this respect, the Theseus paradox certainly does not seem to be fully resolved and will probably continue to be the focus of many debates.

Mereology and Natural Language

Understanding mereology is made difficult by the fact that the term "part of" is often used in an ambiguous way in natural language. This need not be a problem if mereology is merely intended to add a nuance to logical considerations. However, it is doubtful whether and how certain expressions from natural language can be translated into mereological predicates.

In his study of the semantics of natural languages, Harry Bunt deals with the question of the mereological perspective on issues such as the difference between mass and number and the grammatical aspect .

literature

• Peter Simons: Parts. A Study in Ontology . Ed .: Oxford Univ. Press. Clarendon Press, Oxford, UK 1987, ISBN 0-19-924146-5 ( laundry slip [accessed March 1, 2016]).

Mereology is understood as a tool for formal metaphysics. Topics of the book: The work of Leśniewski and his students, the connections between mereology and some European philosophers, especially Edmund Husserl; the relationships between mereology and recent work in formal ontology and metaphysics; Mereology, free logic and modal logic ; Mereology, Boolean algebra and lattice theory

• Marco Aiello: Roberto Casati and Achille Varzi, Parts and Places, The Structures of Spatial Representation . In: Journal of Logic, Language and Information . tape 10 , no. 2 . Kluwer Academic Publishers, 2001, ISSN  0925-8531 , p. 269-272 , doi : 10.1023 / A: 1008366402139 .

Casati and Varzi interpret mereology as a possibility to open up the material world as well as the human relationship to the world. Topics of the book: topology and mereotopology; Margins and holes, the mereological conclusions from Whitehead's process and reality and the works based on it; Mereology as event theory ; Mereology as the "proto-geometry" of physical objects; Mereology and theoretical computer science .

further reading

• Harry Bunt: Mass Terms and Model-Theoretic Semantics . Cambridge Univ. Press, 1985.
• R. Casati, A. Varzi: Parts and Places: The Structures of Spatial Representation . MIT Press, 1999.
• Itamar Francez, Andrew Koontz-Garboden, A Note On Possession and Mereology in Ulwa Property Concept Constructions. In: Natural Language and Linguistic Theory . Vol. 24-1, 2016, pp. 93-106.
• Nelson Goodman: The Structure of Appearance . Harvard Univ. Press, 1951.
• Edmund Husserl: Logical Investigations. Second part: investigations into the phenomenology and theory of knowledge . 1901.
• Stanisław Leśniewski: Outlines of a New System of Foundations of Mathematics. In: Fundamenta Mathematicae . XIV, 1929, pp. 1-81.
• Richard M. Martin: Metaphysical Foundations. Mereology and Metalogic . Philosophia Verlag, 1988.
• Lothar Ridder: Mereology. A contribution to ontology and epistemology . Klostermann, 2002.
• Peter Simons: Parts. A Study in Ontology . Oxford Univ. Press, 1987.
• Alfred North Whitehead: Process and Reality: Designing a Cosmology . Suhrkamp, ​​1987.

See also

• Knowledge representation
• Meronymy
• Aggregation (computer science)

Web links

• Achille Varzi:  Mereology. In: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
• Stanisław Leśniewski: Outlines of a New System of Foundations of Mathematics. (PDF document; 5.20 MB).
• Itamar Francez, Andrew Koontz-Garboden: A Note On Possession and Mereology in Ulwa Property Concept Constructions. doi: 10.1007 / s11049-015-9299-3 .

Individual evidence

1. ↑ Edmund Husserl: Investigations on the phenomenology and theory of knowledge. Second volume. First part. 1901. Ursula Panzer (ed.): Text of the 1st and 2nd edition supplemented by annotations and supplements from the personal copy. Martinus Nijhoff Publishers, The Hague 1984, pp. 267-269.
2. ^ Lothar Ridder: Mereology. A contribution to ontology and epistemology. Klostermann, Frankfurt am Main 2002, p. 1.
3. ↑ Peter Schroder-Heister: Set theory. In: Jürgen Mittelstraß (Hrsg.): Encyclopedia Philosophy and Philosophy of Science. Volume 5: Log-N. Metzler, Stuttgart 2013, pp. 330–331.
4. ^ Lothar Ridder: Mereology. A contribution to ontology and epistemology. Klostermann, Frankfurt am Main 2002, p. 19.
5. ↑ Frank Krickel: Part and epitome. Bernard Bolzano's Mereology. Academia, Sankt Augustin 1995, pp. 291-292.
6. ^ Lothar Ridder: Mereology. A contribution to ontology and epistemology. Klostermann, Frankfurt am Main 2002, p. 66.
7. ^ Peter Simons: Parts. A Study in Ontology. Clarendon, Oxford 1987, pp. 146-147.
8. ^ Kuno Lorenz: Mereology. In: Jürgen Mittelstraß (Hrsg.): Encyclopedia Philosophy and Philosophy of Science. Volume 5: Log-N. Metzler, Stuttgart 2013, p. 342.
9. ^ Peter Simons: Parts. A Study in Ontology . Clarendon, Oxford 1987, pp. 9-18 and p. 362.
10. ↑ Frank Krickel: Part and epitome. Bernard Bolzano's Mereology . Academia, Sankt Augustin 1995, pp. 291-294.
11. ↑ ^{a b c} Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 1–3.
12. ↑ Cian Dorr, Rosen, Gideon: Composition as a fiction, pp. 10-12. In: Richard Gale (Ed.): The Blackwell Companion to Metaphysics. Blackwell, 2002, pp. 151-174. Retrieved from https://philpapers.org/rec/DORCAA on August 18, 2017
13. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, p. 253.
14. ^ David Lewis: On the Plurality of Worlds . Basil Blackwell, New York 1986, p. 213.
15. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, p. 254.
16. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 252-254.
17. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 254-257.
18. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 271-272.
19. ^ David M. Armstrong: A world of states of affairs . Cambridge Univ. Press, 1997, p. 13.
20. ^ David Lewis: On the Plurality of Worlds . Basil Blackwell, New York 1986, p. 212.
21. ↑ ^{a b} Peter Van Inwagen: Material beings. Cornell University Press, Ithaca 1990, p. 31.
22. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 42–43 and p. 49.
23. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 96–97.
24. ↑ ^{a b} The example was taken from: Cian Dorr, Gideon Rosen: "Composition as a fiction", pp. 1–3 In: Richard Gale (ed.): The Blackwell Companion to Metaphysics. Blackwell, 2002, pp. 151-174. Retrieved from https://philpapers.org/rec/DORCAA on August 18, 2017
25. ↑ Harry Deutsch: Relativ Identity. In: Stanford Encyclopedia of Philosophy. 2007. Retrieved from https://plato.stanford.edu/entries/identity-relative/ on August 16, 2017
26. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 230-231.
27. ^ Lothar Ridder: Mereology. A contribution to ontology and epistemology. Klostermann, Frankfurt am Main 2002, p. 107.
28. ↑ Johannes Huebner: Complex substances. de Gruyter, Berlin 2007, p. 243, emphasis in the original
29. ^ Lothar Ridder: Mereology. A contribution to ontology and epistemology . Klostermann, Frankfurt am Main 2002, pp. 107-108.
30. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, p. 132 and p. 230–232 and p. 242–244.
31. ↑ Johannes Huebner: Complex substances . de Gruyter, Berlin 2007, pp. 243–244.