Diffusivity
Diffusivity (from the Latin diffundere “to expand, disperse; let flow out”) is the property of a material that enables dissolved substances to spread. The propagation process itself is known as diffusion .
The term stands on the one hand for the diffusion coefficient , but especially in solid material in the figurative sense for the ability to allow diffusion . In the transferred meaning it is used in particular in the neurosciences in connection with body tissue and the tissue fluid contained in it , but also in hydrology (groundwater), solid-state physics and thermodynamics ( heat diffusivity ).
In contrast to diffusion in liquid or gaseous media, a dissolved substance in a solid (e.g. due to the crystal lattice structure), but also liquid in solid material (e.g. due to soil layers, nerve fibers) generally cannot move in all directions spread equally. Certain directions are preferred and there is anisotropy . In this case, Fick's 1st law replaces the diffusion coefficient with the diffusion tensor (a symmetrical 3 × 3 matrix with real nonnegative eigenvalues).
The direction-dependent propagation in the tissue is known as apparent diffusion , the main diagonal elements of the diffusion tensor as apparent diffusion coefficient (also ADC for apparent diffusion coefficient ). For the quantitative description of the apparent diffusion and the associated anisotropy, various metrics are used which, among other things, are formed from the eigenvalues of the diffusion tensor. So z. B. the fractional anisotropy (FA), how much the eigenvalues differ from each other, d. That is, how much the diffusivity differs in different directions. Fractional anisotropy and relative anisotropy (RA), along with mean , axial, and radial diffusivity , are discussed below.
In the humanities , the term is applied to the degree to which something can spread or shift or be applied to other areas.
background
Diffusion of solutes is described by Fick's laws . The first of these two laws
states that the particle current density depends linearly on the gradient of the concentration : the greater the difference in the concentration of the dissolved substance at two locations, the more particles will flow from the higher to the lower concentration. The coefficient is called the diffusion coefficient or diffusivity.
This description can be used for a wide variety of transport processes, ranging from chemical substances dissolved in liquids to electrical conduction and thermal conduction.
However, the simple description by the one-dimensional law above always collapses when the transport can take place preferentially in certain directions, but is hindered in others. One then speaks of directional dependence or anisotropy .
Possible reasons for anisotropy can be that certain points in the solid can absorb larger concentrations of the dissolved substance. For example, higher concentrations of dissolved hydrogen can accumulate in steel at the crack tip of dislocations . Even when describing the heat conduction play differences between the heat capacity of the material involved, and therefore between the thermal diffusivity (also called the thermal diffusivity) and thermal conductivity must be distinguished.
However, the directional dependency is much more drastic in body tissue, in which cell membranes already hinder the free flow of tissue fluid in healthy tissue .
In the case of anisotropy, the one-dimensional law above takes the place
in that now
is a 3 × 3 matrix called a diffusion tensor . This matrix is symmetrical and therefore has only six independent components, which in a variant of Voigt's notation are called a vector
can be written.
The eigenvalues of the diffusion tensor are denoted by , and , where λ 1 ≥ λ 2 ≥ λ 3 ≥ 0 applies. If the apparent diffusion coefficients are plotted over the respective spatial directions, an ellipsoid of revolution is generally obtained .
Measurement and application
The diffusivity is measured with the help of magnetic resonance imaging (MRI) in so-called diffusion tensor imaging ( DTI) so that the brain is divided into 0.5–8 mm³ large voxels and the diffusion coefficient of self diffusion in each voxel in at least six different directions of water in the tissue fluid is measured. Such a diffusion coefficient is called an apparent diffusion coefficient (also ADC for apparent diffusion coefficient ). On the basis of these at least 6 values per voxel, a diffusion tensor is calculated for each voxel. From this, voxel-wise measures for the diffusivity or anisotropy are derived and z. B. graphically represented with the help of tensor glyphs or as color value images or used for further evaluations, e.g. B. the creation of models of the fiber tracts ( tractography ).
Other properties of the tissue can be deduced from the diffusivity. In this way, conclusions can be drawn about the coarse structure (e.g. fibrous structure) and thus on age- or disease-related changes (e.g. changes in the myelination of the axons ) of brain tissue. Since the mobility of tissue fluid in fibrous tissue in the direction of the tissue fibers is significantly greater than across the fiber direction, models of the brain's fiber tracts can be created on the basis of diffusivity measurements (tractography). However, it can also be determined at which point liquid can flow freely due to the rupture of a membrane.
Dimensions
The diffusivity is described with the eigenvalues of the diffusion tensor, whereby the mean diffusivity , the axial diffusivity and the radial diffusivity are emphasized.
In order to describe the degree of anisotropy, the scale-invariant ratios are also formed from the eigenvalues
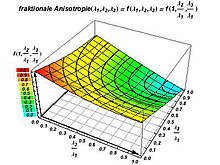
- fractional anisotropy
- relative anisotropy
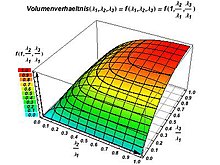
- Volume ratio
Medium diffusivity
The mean diffusivity (the mean diffusion coefficient) is defined as
- (= Mean of the 3 eigenvalues)
In theory, it can be of any size, which would mean any size of diffusivity. for complete absence of apparent diffusion (no Brownian motion of the measured molecules).
Axial diffusivity
The axial diffusivity is the largest of the three eigenvalues.
More clearly: the axial diffusivity is the length of the diffusion tensor ellipsoid and thus describes the strength of the apparent diffusion in the main direction, i.e. the direction of greatest mobility. It is a marker of axonal integrity. The greater the axial diffusivity, the more intact the axons are.
Radial diffusivity
The radial diffusivity is the mean value of the two smaller eigenvalues, i.e. more clearly: The radial diffusivity λ t (t for transversal) is the average thickness of the diffusion tensor ellipsoid in the longitudinal center and describes the average apparent diffusion in the plane perpendicular to the main direction. For example, it is a marker for the integrity of myelin . Demyelination increases radial diffusivity.
Fractional anisotropy
The fractional anisotropy is defined as
More descriptive: The fractional anisotropy FA is the standard deviation of the eigenvalues divided by the mean value of the eigenvalue squares. It is a measure of the directionality of the apparent diffusion. It is FA = 0 in the case of complete isotropy , i.e. H. λ 1 = λ 2 = λ 3 > 0. With maximum anisotropy (complete directionality of the diffusion in exactly one direction), i.e. when λ 1 > 0 and λ 2 = λ 3 = 0, FA = 1. It is, for example a marker for the anatomical nature of the brain's white matter : the larger the FA, the more intact the white matter.
Relative anisotropy
The relative anisotropy is defined as
More illustrative: The relative anisotropy RA is the standard deviation of the eigenvalues (calculated as the standard deviation of a population, i.e. with n = 3 as a divisor) divided by the mean value of the eigenvalues. It is a measure of the directionality of the apparent diffusion. It is RA = 0 in the case of complete isotropy , i.e. H. λ 1 = λ 2 = λ 3 > 0. With maximum anisotropy (complete directionality of the diffusion in exactly one direction), i.e. when λ 1 > 0 and λ 2 = λ 3 = 0, RA = .
Volume ratio
The volume ratio is defined as
More illustrative: The volume ratio VR is the product of the eigenvalues divided by the 3rd power of the mean value of the eigenvalues. It is a measure of the directionality of the apparent diffusion. It is VR = 1 in the case of complete isotropy , i.e. H. λ 1 = λ 2 = λ 3 > 0. If at least the smallest of the eigenvalues equals 0, then VR = 0. This corresponds to the situation that the diffusion only occurs in exactly one direction (λ 2 = λ 3 = 0) or but only takes place in one plane (λ 3 = 0).
literature
- Scott A. Huettel, Allen W. Song, Gregory McCarthy: Functional magnetic resonance imaging . Sinauer Associates, Sunderland, Mass. 2008, ISBN 978-0-87893-286-3 (English-language textbook, explains diffusion tensor imaging in Chapter 5).
- Derek K. Jones: Gaussian Modeling of the Diffusion Signal . In: Heidi Johansen-Berg, Timothy EJ Behrens (Ed.): Diffusion MRI: from quantitative measurement to in-vivo neuroanatomy . Academic Press, London 2009, ISBN 978-0-12-374709-9 , pp. 37–54 ( limited preview in Google Book Search - Chapter 3 in an English-language textbook).
- Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H: Diffusion Tensor Imaging: Concepts and Applications . In: Journal of Magnetic Resonance Imaging . 2001, p. 534–546 (English, Diffusion Tensor Imaging: Concepts and Applications ( Memento from October 19, 2013 in the Internet Archive ) [PDF; 696 kB ; retrieved on June 22, 2016] Review article in specialist journal).
Individual evidence
- ^ Charles Kittel: Thermodynamics . Oldenbourg, Munich 2001, ISBN 3-486-25716-1 , p. 391 ( limited preview in Google Book search).
- ↑ Kurt Krenn: Mediation and Difference? On the meaning of being in the state of participation in St. Thomas Aquinas (= Analecta Gregoriana . Volume 121 ). Editrice Pontificia Università Gregoriana, Rome 1962, ISBN 978-88-7652-094-5 , p. 76, 78 ( limited preview in Google Book search).
- ↑ Gabriele Fassauer: Work performance, identity and market - An analysis of market-like performance control in work organizations . VS Verlag für Sozialwissenschaften, Wiesbaden 2008, ISBN 978-3-531-15950-8 , p. 238 ( limited preview in Google Book search).
- ^ Daniel Fulda: Science from Art - The Origin of Modern German Historiography 1760-186 . W. de Gruyter, Berlin / New York 1996, ISBN 978-3-11-015014-8 , pp. 227 ( limited preview in Google Book search).
- ↑ Guido Juilfs: The diffusion behavior of hydrogen in a low-alloy steel taking into account the degree of deformation . GRIN Verlag, Munich 2008, ISBN 978-3-640-20251-5 , p. 11 ( limited preview in Google Book search).
- ↑ Timo Krings: Basics of functional magnetic resonance imaging . In: Günter Schiepek, Canan Basar (Ed.): Neurobiology of Psychotherapy . Schattauer, Stuttgart 2004, ISBN 3-7945-2363-6 , p. 104–130, especially p. 124 ( limited preview in Google book search).