Euler's polyhedron substitute

The convex icosahedron fulfills Euler's polyhedron substitute.

A non-convex polyhedron with 12 vertices, 36 edges and 32 faces for which does not apply

{\ displaystyle E-K + F = 2}

The star tetrahedron , a concave polyhedron with 14 corners, 36 edges and 24 faces, applies to

{\ displaystyle E-K + F = 2}

The Euler Polyedersatz (also: Euler's formula ), named after Leonhard Euler , a fundamental property of bounded, convex polyhedra and general of planar graphs .

The topological concept of the Euler-Poincaré characteristic is behind the formula . Euler's polyhedron formula is the special case , so it applies generally to polyhedra of characteristic 2, which include the convex polyhedra (but also some non-convex ones). ${\ displaystyle \ chi}$ ${\ displaystyle \ chi = 2}$

General

The theorem says: Let be the number of vertices , the number of edges and the number of faces of a bounded convex polyhedron, then: ${\ displaystyle E}$ ${\ displaystyle K}$ ${\ displaystyle F}$

{\ displaystyle E-K + F = 2}

In words: the number of corners minus the number of edges plus the number of faces equals two.

As an example, the following table lists the five Platonic solids with the associated values for , and . Euler's substitute for polyhedra does not only apply to regular, but to all bounded convex polyhedra. From the sentence it can be deduced that there cannot be more than five platonic solids. ${\ displaystyle E}$ ${\ displaystyle K}$ ${\ displaystyle F}$

polyhedron	E.	K	F.	E - K + F
Tetrahedron	04th	06th	04th	2
cube	08th	12	06th	2
octahedron	06th	12	08th	2
Dodecahedron	20th	30th	12	2
Icosahedron	12	30th	20th	2

history

Euler first mentioned the theorem in a letter to Christian Goldbach in 1750 and published a proof in 1758, but by today's standards for the rigor of mathematical proofs it contained an error, as pointed out by Henri Lebesgue in 1924. It later became known that the sentence was already known to René Descartes (unpublished), which is why it is also known in French literature as the "Theorem of Descartes and Euler". Euler's proof uses the decomposition of a polyhedron into tetrahedra, eliminating one corner at a time. The first rigorous proof was published by Adrien-Marie Legendre in 1794, in his book Élements de Géométrie. Legendre's proof uses the area formula of a geodetic triangle on the surface of a sphere. A correct proof was also found by Augustin Louis Cauchy in 1811, published in 1813. Many different proofs are known to this day.

Ludwig Schläfli and Henri Poincaré (1895) found a generalization to -dimensional polyhedra . Poincaré also recognized the full topological meaning of the sentence. ${\ displaystyle n}$

Generalization to planar graphs

A planar graph with no underlying polyhedron

From polyhedron to planar graph

If a polyhedron has a connected interior without holes, the relationship of its surfaces, edges and corners can also be represented as a planar graph (a flat, connected network, the edges of which do not intersect).

This can be illustrated as follows: If you remove a surface of the polyhedron and pull the adjacent edges apart, you can project the mesh of the polyhedron onto a plane and convert it into a planar graph. Not all regularities of the polyhedron are necessarily preserved - the surfaces that are created do not even have to be polygons - but the number of corners, edges and surfaces (including the outer surface) and the structure of the network are preserved.

Euler's polyhedron substitute for planar graphs

For connected planar graphs, a generalized version of Euler's polyhedron theorem can be formulated. There the areas replace the areas and it applies

Knots - number of edges + area number is 2,

The outer area is counted as part of the area number.

This formulation expands the scope of the theorem to include a large number of non-convex polyhedra as well as planar graphs that are not based on any polyhedra.

If Euler's polyhedron substitution is proven first for planar graphs, the classical polyhedron substitution results from this as a special case.

The Euler characteristic

A more far-reaching generalization of the concept can be found in the Euler characteristic of a closed surface . From this point of view, the convexity of the polyhedron is only a (strong) sufficient requirement to ensure that the surface of the polyhedron is homeomorphic to the 2-sphere .

A classic proof

The simplest graph	Creation of the cube network
Adding a corner with an edge	Add an edge

This proof shows the validity of the theorem for planar graphs with structural induction .

The simplest planar graph consists of just one corner. There is a face (the outer face) and no edges. So it applies . From this simplest graph, all others can be constructed exclusively by the following two operations , which do not change the validity of the theorem: ${\ displaystyle E-K + F = 1-0 + 1 = 2}$

Adding a corner that is connected to the rest of the graph by a new edge. The number of corners and edges increases by one while the number of faces remains the same. If it was true for the old graph , it is also true for the new one, since one each was added and subtracted on the left side of the equation. ${\ displaystyle E-K + F = 2}$
Adding an edge that connects two already existing corners. While the number of corners remains the same, the number of faces and edges increases by one. Again, the total remains the same because a one has been added and subtracted. ${\ displaystyle E-K + F}$

Since the theorem applied to the first, simplest graph, it must also apply to every graph that is created from it by one of the two operations. Every graph that arises from such a graph through a further operation must also satisfy the theorem, and so on. Therefore, the theorem applies to all planar graphs and therefore also to all convex polyhedra.

The proof is from Cauchy. He was the first to reduce the problem to that of graph theory.

Unusual evidence

Polyhedron and associated planar graph - embedded in a grid

This proof shows the validity of the theorem for planar graphs using Pick's theorem . Conversely, Pick's theorem can also be derived from Euler's polyhedron substitution, so that both are equivalent.

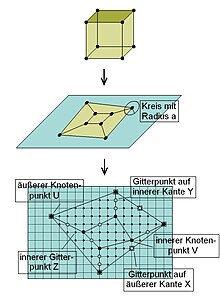
In order to be able to apply Pick's theorem, the graph must be embedded in a grid so that the nodes of the graph lie on grid points. The graph remains equivalent if one moves each node within a suitably small neighborhood. Let the radius of the smallest circle around a node that is completely embedded in the environment be . Any grid with unity on the plane is considered. Then we can move each nodal point to a grid point and surely get an equivalent graph. The planar graph now has a total of nodes, edges and inner surfaces. ${\ displaystyle a}$ ${\ displaystyle a}$ ${\ displaystyle E}$ ${\ displaystyle K}$ ${\ displaystyle F-1}$

The total (inner) area of the planar graph can be determined in two ways using Pick's theorem . First of all, all grid points within or on the graph must be characterized. The points within are divided into three categories: nodes , points on edges and other ; the points on the edge in nodes and points on edges . Let the number of points be . Obviously then applies to the number of vertices or nodes . ${\ displaystyle A}$ ${\ displaystyle V}$ ${\ displaystyle Y}$ ${\ displaystyle Z}$ ${\ displaystyle U}$ ${\ displaystyle X}$ ${\ displaystyle U, V, X, Y, Z}$ ${\ displaystyle u, v, x, y, z}$ ${\ displaystyle E = u + v}$

(i) Let us consider the graph without its exact internal structure: There are then a total of grid points inside and points on the edge. According to Pick's theorem, the area of the graph is: ${\ displaystyle v + y + z}$ ${\ displaystyle u + x}$

{\ displaystyle A = \ left (v + y + z \ right) + {\ frac {1} {2}} \ left (u + x \ right) -1}

(ii) The area can also be calculated by adding up the areas of the inner areas of the graph using Pick's theorem. The sum of all inner points is then natural . The grid points on the edges and the nodes of the graph lie on one or more edges of the areas and therefore appear several times in the sum over the areas. ${\ displaystyle A}$ ${\ displaystyle F-1}$ ${\ displaystyle z}$ ${\ displaystyle F-1}$ ${\ displaystyle F-1}$

The grid points on edges in the interior (points ) each belong to two surfaces, so they appear twice in the sum. The grid points on edges at the edge (points ) occur only once. ${\ displaystyle Y}$ ${\ displaystyle X}$

Let us now consider the inner nodes . They border on as many inner areas as there are edges leading away from them. At the nodes on the edge there is one more edge than adjacent inner surfaces. If one adds the number of leading edges over all nodes, one obtains that each edge occurs twice. If you add the number of adjacent inner surfaces over all nodes, you get that the number of leading edges corresponds to the number of adjacent surfaces except for a 1 at the nodes at the edge. The nodal points therefore occur a total of times over all areas . ${\ displaystyle V}$ ${\ displaystyle U}$ ${\ displaystyle 2K}$ ${\ displaystyle 2K-u}$ ${\ displaystyle u}$ ${\ displaystyle F-1}$ ${\ displaystyle (2K-u)}$

With the application of Pick's theorem, the following applies to the area of the graph : ${\ displaystyle (F-1)}$

{\ displaystyle A = z + {\ frac {1} {2}} \ left (2y + x + 2K-u \ right) - (F-1)}

By equating the two surface formulas (i) and (ii), the terms with drop out, and one directly obtains the Euler's polyhedral formula with: ${\ displaystyle x, y, z}$ ${\ displaystyle E = u + v}$

{\ displaystyle E + F = K + 2}

Proof according to von Staudt

Karl von Staudt gave a simple, non-recursive proof in his geometry of the situation in 1847 .

To do this, consider the graph of the planar projection of the polyhedron, which has nodes, edges and surfaces. The graph is connected for the considered polyhedra and thus has a spanning tree . Since it contains exactly nodes and is a connected tree (without a cycle), it has edges. Now consider the dual graph , formed from the centers of the surfaces of , and connect these with edges in such a way that they do not intersect the edges . This line of edges is connected because it does not contain any circles. It is also a tree, otherwise it would contain a circle (cycle) that divides the nodes of into two parts and thus intersects an edge of , contrary to the construction requirement. thus has nodes and edges. The edges in are composed of the edges of or are crossed by an edge of , so the following applies . ${\ displaystyle P}$ ${\ displaystyle E}$ ${\ displaystyle K}$ ${\ displaystyle F}$ ${\ displaystyle T}$ ${\ displaystyle T}$ ${\ displaystyle E}$ ${\ displaystyle E-1}$ ${\ displaystyle P}$ ${\ displaystyle Q}$ ${\ displaystyle P}$ ${\ displaystyle T}$ ${\ displaystyle S}$ ${\ displaystyle T}$ ${\ displaystyle P}$ ${\ displaystyle T}$ ${\ displaystyle S}$ ${\ displaystyle F}$ ${\ displaystyle F-1}$ ${\ displaystyle P}$ ${\ displaystyle T}$ ${\ displaystyle S}$ ${\ displaystyle K = E-1 + F-1 = E + F-2}$

literature

David Richeson: The polyhedral formula. In: Robert Bradley, Edward Sandifer (Eds.): Euler: Life, Work, Legacy. Elsevier, 2007.
David Richeson: Euler's acc. Princeton University Press, 2008.

Web links

20 different proofs in English, including the unusual proof given above using Pick's theorem .
Eric W. Weisstein : Polyhedral Formula . In: MathWorld (English).
Abigail Kirk: Euler's Polyhedron Formula. Plus Magazine, 2007.

Individual evidence

↑ Louis Poinsot first pointed this out in 1810.
↑ Euler: Elementa doctrine solidorum. In: Novi comm. acad. scientiarum imperialis petropolitanae. 4, 1758, pp. 72-93 (Eneström Index E 230). Euler: Demonstratio nonnullarum insignium proprietatum quibus solida hedris planis inclusa sunt praedita. In: Novi Commentarii Academiae Scientiarum Petropolitanae. 4, 1758, pp. 94-108 (his proof, E 231). Reprinted in Opera Omnia. Volume 26. The two works date from 1750 and 1751 respectively.
^ E. de Jonquières: Note sur une pointe fundamental de la théorie des polyèdres. In: Comptes Rendus Acad. Sci. Paris, 110, 1890, pp. 110-115. From writings left behind by Descartes, only survived from a copy by Gottfried Wilhelm Leibniz , discovered in the Hanover State Library in 1860. Richeson: The polyhedral formula. See literature.
↑ Represented in David Richeson: Eulers gem. Princeton University Press 2008, Chapter 7, pp. 67 ff.
^ Cauchy: Recherches sur les polyèdres. In: J. Ecole Polytechnique. 9, 1813, pp. 68-98.
↑ David Richeson: Euler's gem. Princeton University Press, 2008, chapter 12.
↑ D. DeTemple, JM Robertson: The equivalence of Euler's and Pick's theorems. In: American Mathematical Monthly. Volume 98, 1991, pp. 97-108.
↑ For example: Aigner, Ziegler: Proofs from the Book. Springer Verlag, 2010, Chapter 12, Three applications of Euler's Formula. David Richeson: The polyhedral formula. In: Bradley, Sandifer: Euler. Elsevier, 2007, p. 434. It is also presented in HSM Coxeter : Regular Polytopes . Here in the graph theory version by Aigner, Ziegler.
↑ Historically, Staudt derived a criterion for the polyhedra to which the sentence applies.

[1] Louis Poinsot first pointed this out in 1810.

[2] Euler: Elementa doctrine solidorum. In: Novi comm. acad. scientiarum imperialis petropolitanae. 4, 1758, pp. 72-93 (Eneström Index E 230). Euler: Demonstratio nonnullarum insignium proprietatum quibus solida hedris planis inclusa sunt praedita. In: Novi Commentarii Academiae Scientiarum Petropolitanae. 4, 1758, pp. 94-108 (his proof, E 231). Reprinted in Opera Omnia. Volume 26. The two works date from 1750 and 1751 respectively.

[3] E. de Jonquières: Note sur une pointe fundamental de la théorie des polyèdres. In: Comptes Rendus Acad. Sci. Paris, 110, 1890, pp. 110-115. From writings left behind by Descartes, only survived from a copy by Gottfried Wilhelm Leibniz , discovered in the Hanover State Library in 1860. Richeson: The polyhedral formula. See literature.

[4] Represented in David Richeson: Eulers gem. Princeton University Press 2008, Chapter 7, pp. 67 ff.

[5] Cauchy: Recherches sur les polyèdres. In: J. Ecole Polytechnique. 9, 1813, pp. 68-98.

[6] David Richeson: Euler's gem. Princeton University Press, 2008, chapter 12.

[7] D. DeTemple, JM Robertson: The equivalence of Euler's and Pick's theorems. In: American Mathematical Monthly. Volume 98, 1991, pp. 97-108.

[8] For example: Aigner, Ziegler: Proofs from the Book. Springer Verlag, 2010, Chapter 12, Three applications of Euler's Formula. David Richeson: The polyhedral formula. In: Bradley, Sandifer: Euler. Elsevier, 2007, p. 434. It is also presented in HSM Coxeter : Regular Polytopes . Here in the graph theory version by Aigner, Ziegler.

[9] Historically, Staudt derived a criterion for the polyhedra to which the sentence applies.