Projective geometry

projective theorem of Desargues

The projective geometry is a branch of geometry . It emerged from the perspective representation of three-dimensional objects in the two-dimensional plane. In contrast to "ordinary" Euclidean geometry, there are no parallels in projective geometry .

Projective geometry, like affine geometry, deals with points, straight lines, planes, curves and surfaces; but without the parallelism of straight lines. So there are no parallel projections , only central projections . The objects to be examined now lie in a projective plane or a projective space . Mostly one deals with objects in a projective space above the real numbers or the complex numbers , that is, the coordinates of the points are real or complex numbers. Only in axiomatic projective geometry (see below) do coordinates from more general structures ( bodies , oblique bodies , ternary bodies , ...) occur. Projective planes / spaces, in which Desargues' theorem applies, can still be well described with the help of vector spaces using oblique bodies. This shows the great importance of Desargues' theorem. However, it always applies in at least 3-dimensional projective spaces. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {C} }$

For the sake of simplicity, real coordinates are always assumed here up to the section on axiomatic projective geometry.

motivation

Central projection of parallel straight lines

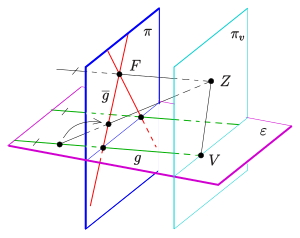
A parallel projection of one plane onto another preserves the parallelism of the straight line. With a central projection (see picture) this is i. A. no longer the case. In the picture, the two green parallel straight lines of the horizontal plane are mapped through the central projection with the center on two (red) straight lines of the vertical plane that intersect at the point . The point , however, has no archetype. It is called the vanishing point of the green set of parallels. On the other hand, the point (in the plane to be parallel ) of the straight line has no image. One calls the vanishing point of the straight line . A central projection is therefore not a bijection (1-1 figure) of the plane onto the plane . The way out of this dilemma: Add another point to each parallel array in each plane so that parallel lines intersect. These new points are called far points and the set of far points forms the distance line of the respective plane. The far point of the straight line is then mapped onto the vanishing point in the image. The point of disappearance is mapped to the far point of the (red) straight line . Adding the far points to a plane creates a new incidence structure with the typical properties ${\displaystyle \varepsilon }$ ${\displaystyle Z}$ ${\displaystyle F}$ ${\displaystyle \pi }$ ${\displaystyle F}$ ${\displaystyle V}$ ${\displaystyle \pi }$ ${\displaystyle \pi _{v}}$ ${\displaystyle g}$ ${\displaystyle V}$ ${\displaystyle g}$ ${\displaystyle \varepsilon }$ ${\displaystyle \pi }$ ${\displaystyle g}$ ${\displaystyle F}$ ${\displaystyle V}$ ${\displaystyle {\overline {g}}}$

(1): every two points have exactly one connecting line and

(2): every two straight lines have exactly one point of intersection .

This new structure is called the real projective plane .
This way of extending an affine plane is called projective closure .

Principle of duality

Reversed one (s. O.) In the incidence of properties (1), (2) the terms straight and point , and cutting and joining , so only the statements of (1) and (2) are reversed. So if you have a statement that only uses the terms straight line, point, intersect and connect, its dual statement also applies. For example, by dualizing Pascal 's theorem , one obtains Brianchon's theorem . The set of Desargues is equal to its dual statement. But Pappus' dual theorem is another statement about projective planes.

The duality principle does not apply to affine levels .

Inhomogeneous coordinates of a real projective plane

Inhomogeneous coordinates

In order to assign coordinates to a point of a real projective plane, one describes a finite point (not a far point) in the usual way . The slope (including ) is suitable for the far point of the straight line (see picture). Since a point is described either by two coordinates or by one coordinate (far point), these coordinates are called inhomogeneous coordinates . Compared to homogeneous coordinates, inhomogeneous coordinates have the big advantage: They are unique and you can calculate in the usual way in the finite range. ${\displaystyle (x,y)}$ ${\displaystyle y=mx+b}$ ${\displaystyle (m)}$ ${\displaystyle \infty }$

Homogeneous coordinates

Relationship between inhomogeneous and homogeneous coordinates

That the real projective plane in its inhomogeneous description is only formally an inhomogeneous structure is shown by its description with homogeneous coordinates . To do this, one defines in ${\displaystyle \mathbb {R} ^{3}}$

every straight line through the origin is a (projective) point and

every plane of origin is a (projective) straight line .

A point is incised with a straight line if the straight line through the origin corresponding to the point lies in the plane of origin corresponding to the straight line. It can be shown that the incidence structure defined in this way is geometrically equivalent, isomorphic , to the model of the real projective plane defined above . The picture shows the embedding of the finite points of the inhomogeneous model of the real projective plane in the plane with the equation . The plane takes on the role of the straight line . Every straight line through the origin of this plane is a far point. The picture shows the assignment of the far points of both models. Since a point different from the zero point describes a straight line through the origin and thus a point of the projective plane, its homogeneous coordinates are called and ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle x_{3}=1}$ ${\displaystyle x_{3}=0}$ ${\displaystyle (x_{1},x_{2},x_{3})\in \mathbb {R} ^{3}}$ ${\displaystyle x_{1},x_{2},x_{3}}$

denotes the (projective) point with . ${\displaystyle (x_{1}:x_{2}:x_{3})}$

Since a straight line through the origin can be described by any point on it other than the zero point, the following applies

${\displaystyle (tx_{1}:tx_{2}:tx_{3})=(x_{1}:x_{2}:x_{3})}$.

That is, homogeneous coordinates do not uniquely describe the points of the real projective plane . This is a disadvantage compared to inhomogeneous coordinates. A straight line (plane of origin) is described in the homogeneous model by an equation . ${\displaystyle ax_{1}+bx_{2}+cx_{3}=0}$

The coordinates of finite points (not far points) can be converted by

${\displaystyle (x,y)\ \leftrightarrow \ (x:y:1)\quad }$ or. ${\displaystyle \quad (x_{1}:x_{2}:x_{3})\ \leftrightarrow \ ({\tfrac {x_{1}}{x_{3}}},{\tfrac {x_{2}}{x_{3}}})\ .}$

The big advantage of the homogeneous coordinates is

Each incidence-preserving mapping (collineation) is described by a linear mapping (matrix).

(An affine map is a combination of a linear map and a displacement.)

If one embeds the xy-plane in such a way that it is equal to the plane , the plane of origin becomes the distance line. In this case the homogeneous coordinates are the barycentric coordinates with respect to the triangle . ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle \ x_{1}+x_{2}+x_{3}=1\ }$ ${\displaystyle x_{1}+x_{2}+x_{3}=0}$ ${\displaystyle (1:0:0),(0:1:0),(0:0:1)}$

n-dimensional projective space

The description of the real projective plane with homogeneous coordinates shows that one can define an n-dimensional projective space analogously in : ${\displaystyle \mathbb {R} ^{n+1}}$

The points are the straight lines through the origin of the ${\displaystyle \mathbb {R} ^{n+1}}$

The straight lines are the original planes.

For we get the projective straight line . It is of no interest as an incidence structure, but the group of projective permutations defined here is interesting as a projective linear group . In the homogeneous model, it operates on the straight line through the origin of the as a matrix group or in the inhomogeneous model as broken linear images . An essential property is: ${\displaystyle n=1}$ ${\displaystyle PGL(2,\mathbb {R} )}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle x\mapsto {\tfrac {ax+b}{cx+d}}}$

The group operates sharply 3-fold transitive , i.e. H. for every two triples of points there is exactly one mapping that maps one onto the other. ${\displaystyle PGL(2,\mathbb {R} )}$

Collineation, central collineation, projectivity

Collineation

A collineation of a projective plane is a bijective mapping of the point set to itself, which maps collinear points onto collinear points. permutes both the set of points and the set of straight lines. ${\displaystyle \kappa }$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle \kappa }$ ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {G}}}$

Central collineation: For each point are collinear ${\displaystyle P}$ ${\displaystyle Z,P,\pi (P)}$

Central collineation

Important collineations of a projective plane are the central collineations (also called perspectives ).

A central collineation defines a point, the center , and all straight lines through this point.

One can prove that there is then a straight line, the axis , whose points all remain fixed. However, it can happen that the center is also on the axis. In this case the central collineation is called elation , otherwise homology . If the axis is the distant line, then a central projection in the finite (affine) part is a point extension or a translation (displacement).

Projectivity

Executing several central collineations one behind the other is called projective collineation or projectivity .

The following applies to the real projective plane

(PR) : Every collineation is a projective collineation and can be described in homogeneous coordinates by a linear mapping.

example

The translation is carried out in homogeneous coordinates (see above) ${\displaystyle \ (x,y)\;\to \;(x+s,y+t)\ }$

${\displaystyle (x_{1}\colon x_{2}\colon x_{3})\ \to \ (x_{1}+sx_{3}\colon x_{2}+tx_{3}\colon x_{3})}$

and thus described as a linear mapping with the matrix . ${\displaystyle {\begin{pmatrix}1&0&s\\0&1&t\\0&0&1\end{pmatrix}}\ }$

More examples can be found in the article Homogeneous Coordinates .

The projective collineation group of the real projective plane generated by the 3 × 3 matrices is the projective linear group ${\displaystyle PGL(3,\mathbb {R} ).}$

The property (PK) is not generally valid. For example, there are collineations in the complex projective plane that can only be represented as semi- linear images . For example: ${\displaystyle (x_{1}:x_{2}:x_{3})\ \rightarrow \ ({\overline {x}}_{1}:{\overline {x}}_{2}:{\overline {x}}_{3})\ .}$

Collineation between incidence structures

A projective plane / space can usually be described with at least two models (inhomogeneous, homogeneous). In order to prove that two incidence structures describe the same geometry, it is necessary to provide a bijective mapping of on , which maps collinear points to collinear points. This means that the term collineation has to be expanded accordingly. Generally is ${\displaystyle ({\mathcal {P}}_{1},{\mathcal {G}}_{1}),\;({\mathcal {P}}_{2},{\mathcal {G}}_{2})}$ ${\displaystyle {\mathcal {P}}_{1}}$ ${\displaystyle {\mathcal {P}}_{2}}$

a collineation a mapping from one incidence structure to a second, which maps straight lines on straight lines.

Duality, polarity

A bijective mapping of the points of a projective plane to the set of straight lines , which maps collinear points to co-point straight lines and vice versa, is called duality . ${\displaystyle {\mathcal {P}}}$ ${\displaystyle ({\mathcal {P}},{\mathcal {G}})}$ ${\displaystyle {\mathcal {G}}}$

A duality is thus a collineation of a projective plane on its dual projective plane.

Example: The mapping of the real projective plane, which assigns the plane with the equation to a point (in homogeneous coordinates) , is a duality. ${\displaystyle (a:b:c)}$ ${\displaystyle ax_{1}+bx_{2}+cx_{3}=0}$

Special dualities are polarities:

A duality is polarity when in the incidence of straight line with the following that on lies. is called polar of and pole of . ${\displaystyle \delta }$ ${\displaystyle P}$ ${\displaystyle \delta (Q)}$ ${\displaystyle Q}$ ${\displaystyle \delta (P)}$ ${\displaystyle \delta (P)}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle \delta (P)}$

One polarity is always involutive, i.e. H. Identity. ${\displaystyle \delta ^{2}=}$

The duality in the example above is a polarity.

If a polarity has points that lie on its polar, the polarity is called hyperbolic (e.g. pole-polar relationship to a non- degenerate conic section ), in the other case elliptical .

The above example of polarity is elliptical. However, it is essential that the underlying projective level is the real level! If the coordinates are complex numbers, the polarity is hyperbolic, because in this case the equation has nontrivial solutions: e.g. B. the point lies on its polar . ${\displaystyle x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=0}$ ${\displaystyle (1:i:0)}$ ${\displaystyle x_{1}+ix_{2}=0}$

Double ratio

In the case of projective images in a projective space, the partial ratio is no longer invariant (e.g. the center point of a line no longer merges into the center point of the image line). The analogue to the partial ratio in projective geometry is the double ratio (ratio of two partial ratios).

Im is the division ratio in which a point divides a distance , the number defined by the relationship . ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle (A,B;S)}$ ${\displaystyle S}$ ${\displaystyle AB}$ ${\displaystyle {\overrightarrow {AS}}=\lambda \;{\overrightarrow {SB}}\ }$ ${\displaystyle \lambda }$

Double ratio: definition

Examples

1) Is , then is the midpoint of the line . 2) For divides the route in proportion 3) For lies outside and divides the route in proportion . ${\displaystyle (A,B;S)=1}$ ${\displaystyle S}$ ${\displaystyle AB}$
${\displaystyle (A,B;S)=3}$ ${\displaystyle S}$ ${\displaystyle 3:1}$
${\displaystyle (A,B;S)=-3}$ ${\displaystyle S}$ ${\displaystyle B}$ ${\displaystyle AS}$ ${\displaystyle 2:1}$

Invariance of the double ratio in central projection

Im is the double ratio in which a pair of points divides a distance , the number ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle (A,B;S,T)}$ ${\displaystyle S,T}$ ${\displaystyle AB}$

${\displaystyle (A,B;S,T)=(A,B;S):(A,B;T)}$

(Ratio of two partial ratios).

The double ratio, which was initially only defined for the affine points of the real projective plane / space, can be uniformly expressed in homogeneous coordinates with the help of ratios of determinants (see double ratio ).

The great importance of the double ratio is based on the property

The double ratio is invariant for projectivities .

If the double ratio of two pairs of points is called a harmonic division . If the points lie harmoniously and if the far point of the straight line is, the midpoint of the line is . ${\displaystyle -1}$ ${\displaystyle A,B,S,T}$ ${\displaystyle T}$ ${\displaystyle S}$ ${\displaystyle AB}$

Affine constraint (slitting)

Affine spaces can always be created from a projective space by removing hyperplanes ( slits ). In this way, the results obtained in a projective space can then also be described affinely by a suitable choice of a distance line / hyperplane. So are z. For example, some properties of parabola and hyperbola are simply the affine versions of degenerations of Pascal's theorem for a projective conic section.

Projective conic section, quadrics

Projective conic section in homogeneous coordinates

Projective conic section in inhomogeneous coordinates

Projective conic section

If the parabola is represented in homogeneous coordinates according to the above conversion ( ), the equation is obtained . This equation describes a cone with the tip at the origin. It touches the plane in the -axis. This equation is also fulfilled for the far point (the y-axis). The zero formation of the homogeneous equation consists of the parabolic points plus a far point. ${\displaystyle y=x^{2}}$ ${\displaystyle x={\tfrac {x_{1}}{x_{3}}},y={\tfrac {x_{2}}{x_{3}}}}$ ${\displaystyle x_{1}^{2}-x_{2}x_{3}=0}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle x_{3}=0}$ ${\displaystyle x_{2}}$ ${\displaystyle (0:1:0)}$

One calls the projective curve with the equation and all projective images a non-degenerate projective conic section . ${\displaystyle x_{1}^{2}-x_{2}x_{3}=0}$

(A na projective conic section can also be defined by other properties. For example: Steiner generation, v.Staudt conic section or by symmetries. See the articles on projective conic sections and ovals .)

If the hyperbola is represented in homogeneous coordinates, the equation is obtained . This equation is also fulfilled for the two far points (the x and y axes). It can be seen that this equation merges into the curve resulting from the parabola due to the change in coordinates (linear mapping). It is therefore also a projective conic section. ${\displaystyle y=1/x}$ ${\displaystyle x_{1}x_{2}-x_{3}^{2}=0}$ ${\displaystyle (1:0:0),(0:1:0)}$ ${\displaystyle x_{1}\leftrightarrow x_{3}}$

If you start from the unit circle , you get and from it . This equation can also be transformed into the first equation by a linear mapping. ${\displaystyle x^{2}+y^{2}=1}$ ${\displaystyle x_{1}^{2}+x_{2}^{2}=x_{3}^{2}}$ ${\displaystyle x_{1}^{2}-(x_{3}-x_{2})(x_{3}+x_{3})=0}$

A conic section has a particularly large number of automorphisms (collineations that leave the conic section invariant).

The automorphism group of a projective conic section is isomorphic to the group . (This is triple transitive, i.e. for every two triples of points there is a collineation that maps one triplet onto the other.) ${\displaystyle PGL(2,\mathbb {R} )}$

Projective Quadrics

Analogous to a projective conic section, projective quadrics in projective spaces in homogeneous coordinates can be described as zero point structures of square shapes .

As with conic sections, different quadrics coincide affinely in 3-dimensional projective space. For example: cone and cylinder or ellipsoid and elliptical paraboloid .

Plücker coordinates and Klein quadric

→ Main article : Plücker coordinates

In 3- dimensional real projective space , a point (1-dim. Subspace des ) can be described in homogeneous coordinates by and a plane (3-dim. Subspace) with the equation by the (projective) point . ${\displaystyle P^{3}(\mathbb {R} )}$
${\displaystyle \mathbb {R} ^{4}}$ ${\displaystyle (x_{0}\colon x_{1}\colon x_{2}\colon x_{3})}$
${\displaystyle a_{0}x_{0}+a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}=0}$ ${\displaystyle (a_{0}\colon a_{1}\colon a_{2}\colon a_{3})}$

There is no such simple homogeneous description for the straight lines (planes of origin) that are important in many investigations. Musings of J. Plucker led to the introduction of the eponymous Plucker coordinates :

A straight line is uniquely determined by a pair of points on it. Plücker was able to show that the six 2x2 determinants ${\displaystyle g}$ ${\displaystyle X=(x_{0}\colon x_{1}\colon x_{2}\colon x_{3}),\;Y=(y_{0}\colon y_{1}\colon y_{2}\colon y_{3})}$

${\displaystyle p_{ij}=\left|{\begin{array}{cc}x_{i}&y_{i}\\x_{j}&y_{j}\end{array}}\right|\;,\quad i\neq j\;,\;i,j=0,1,2,3\ ,}$

except for a common multiple, clearly define the straight line through . The straight line can thus be described by the point of the 5- dimensional real projective space . ${\displaystyle X,Y}$ ${\displaystyle {\overline {XY}}}$ ${\displaystyle (p_{01}\colon p_{02}\colon p_{03}\colon p_{12}\colon p_{13}\colon p_{23})}$ ${\displaystyle P^{5}(\mathbb {R} )}$

The points determined by the straight lines do not, however, cover the whole . Because the determinants still have to fulfill the homogeneous quadratic equation, the Plücker relation : ${\displaystyle P^{3}(\mathbb {R} )}$ ${\displaystyle P^{5}(\mathbb {R} )}$

${\displaystyle p_{01}p_{23}+p_{02}p_{13}+p_{03}p_{12}=0}$.

This equation describes a projective quadric in 5-dimensional projective space, which is referred to as a small quadric . Each point of the small quadric represents a straight line of the . ${\displaystyle P^{3}(\mathbb {R} )}$

Applications of the Plücker coordinates can be found in the English article Plücker coordinates .

The concept of Plücker coordinates can be transferred to any 3-dimensional Pappus projective space (the coordinate area is a body).

Homogeneous representation of rational curves

Rational Bezier curve (red) as a projection of an ordinary spatial Bezier curve (blue)

A curve with a rational representation

${\displaystyle \left({\frac {p_{1}(t)}{q_{1}(t)}},{\frac {p_{2}(t)}{q_{2}(t)}}\right)}$

where the functions and are polynomials can be represented polynomially in homogeneous coordinates : ${\displaystyle p_{i}}$ ${\displaystyle q_{i}}$

${\displaystyle (\left(p_{1}(t)q_{2}(t):p_{2}(t)q_{1}(t):q_{1}(t)q_{2}(t)\right)\ .}$

A plane curve with rational coefficient functions can therefore be understood as the central projection of a polynomial curve of the on the embedding plane. ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle x_{3}=1}$

In this way, z. B. represent a rational Bezier curve with the help of a projection of an ordinary (polynomial) Bezier curve. In particular, elliptical and hyperbolic arcs are projections of Bezier curves of degree 2 (parabolas).

Axiomatic projective geometry

In axiomatic projective geometry, one starts with very weak axioms , the incidence axioms . A projective plane defined in this way consists of a set of points and a set of straight lines with the simple incidence properties

(1 :) Every two points have exactly one connecting line and

(2 :) Every two straight lines have exactly one point of intersection .

Such a projective plane is still very far from the real projective plane. It is only through an additional axiom (Pappos' theorem) that such a projective plane can only be described with the help of a vector space over a body and thus linear algebra can be used. To achieve that these fields are even the real numbers, a few more axioms are necessary. (See Hilbert's system of axioms of Euclidean geometry )

Veblen-Young axiom

Since straight lines do not necessarily have to intersect in a projective space , but on the other hand every flat point set should be a projective plane, axiom (2) must be replaced in space by the Veblen-Young axiom :

( Axiom of Veblen-Young ) are , , , four points, making and incident with a common point, so incise also and to a common point ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle AB}$ ${\displaystyle CD}$ ${\displaystyle AD}$ ${\displaystyle BC}$ .

In an at least 3-dimensional projective space, in contrast to the plane case, Desargues' theorem always applies and the space can then be coordinated over a sloping body (not necessarily a commutative body).

In the plane case there are numerous so-called non-desargue projective planes , which are usually represented by a closure sentence, e.g. B. Desargues' small theorem (center is on the axis) or by the richness of the automorphism group (group of collineations on itself). A classification of the non-Desargue levels is provided by the Lenz-Barlotti classification .

Desargues and Pappus' theorems

Desargues theorem

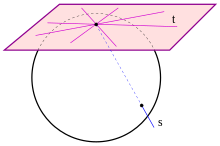
If there are two triangles and a perspective with a center , the points of intersection of the straight lines through corresponding sides are collinear (see first picture above). ${\displaystyle ABC}$ ${\displaystyle A'B'C'}$ ${\displaystyle Z}$ ${\displaystyle U,V,W}$

affine versions of Desargues' theorem

Desaguessche level: introduction of coordinates

The great importance of this theorem consists in the possibility of constructing a projective plane in which the theorem applies to all possible configurations, a sloping body for an inhomogeneous coordination. The projective plane is limited by removing (slitting) a straight line to an affine plane, in which the affine forms of Desargues' theorem apply:

(GD): (large Desargues) If there are two triangles and perspective with a center , the parallelism of two pairs of sides results in the parallelism of the third pair of sides (see picture). ${\displaystyle ABC}$ ${\displaystyle A'B'C'}$ ${\displaystyle Z}$

(KD): (small Desargues) Lying two triangles and parallel to three straight lines, so two side pairs follows from the parallelism, the parallelism of the third pair of sides (see Figure.). ${\displaystyle ABC}$ ${\displaystyle A'B'C'}$

In the now affine plane one chooses two straight lines that intersect at a point . (It becomes the origin of the coordinate system and becomes the x and y axis.) With the help of Desargues' little theorem, one first defines translations and then an addition on the points of the straight line . With the help of the large theorem one constructs point stretching and thus a multiplication . Finally it can be shown that addition and multiplication turn the point set of into a skew. With the help of a parallel projection (red in the picture), this inclined coordinate body can also be transferred to the straight line . A pair of coordinates can then be assigned to each point of the affine plane in the usual way . A straight line is described (as usual) by an equation or . The affine plane coordinated in this way can then be expanded again to an inhomogeneous description of the projective plane by adding far points (see above). The homogeneous display (see above) is also possible. However, since the coordinate inclined body is not necessarily commutative, one must pay attention to the order of the multiplication. ${\displaystyle O}$ ${\displaystyle g_{x},g_{y}}$ ${\displaystyle O}$ ${\displaystyle g_{x},g_{y}}$ ${\displaystyle g_{x}}$ ${\displaystyle g_{x}}$ ${\displaystyle g_{y}}$ ${\displaystyle X}$ ${\displaystyle (x,y)}$ ${\displaystyle y=mx+d}$ ${\displaystyle x=c}$

Pappos' theorem: projective form

Pappos' theorem: affine form

Set of pappus

If six points of a projective plane lie alternately on two straight lines and , then the points are ${\displaystyle P_{1},P_{2},P_{3},P_{4},P_{5},P_{6}}$ ${\displaystyle g}$ ${\displaystyle h}$

${\displaystyle P_{7}={\overline {P_{1}P_{2}}}\cap {\overline {P_{4}P_{5}}},\ }$ ${\displaystyle P_{8}={\overline {P_{6}P_{1}}}\cap {\overline {P_{3}P_{4}}},\ }$ ${\displaystyle P_{9}={\overline {P_{2}P_{3}}}\cap {\overline {P_{5}P_{6}}}}$

collinear, d. i.e., they lie on a straight line (see picture). ${\displaystyle u}$

If the straight line is the distance line, then we get the affine form of the proposition. ${\displaystyle u}$

The meaning of this theorem is that its validity in a Desarguessian plane turns the inclined body into a body (multiplication is commutative). But the meaning of Pappus' theorem is even greater because it applies

( Theorem of Hessenberg ) In a projective plane in which the theorem of Pappus applies, the theorem of Desargues also applies.

That means: A body can be constructed from the sole validity of Pappus' theorem. However, a finite Desarguean plane is always already pappusian, since every finite skew body is commutative (Wedderburn's theorem).

Projective images of rows of points and straight lines

perspective row of points

If two straight lines are on a projective plane and a point that does not lie on both straight lines, then the mapping that maps (projects) a point of the straight line onto the point of intersection is called a perspective mapping (also called perspective assignment ) from onto with a center . ${\displaystyle g,h}$ ${\displaystyle Z}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle \pi (P)=h\cap {\overline {PZ}}}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle Z}$

Executing several such images one behind the other is called a projective image . (Note that we are not talking about a collineation of the projective plane. Only the points of the starting line are mapped onto the points of the target line.)

If the straight line is the same as the straight line (only for real projective images), then applies to the set of all projective images from on itself ${\displaystyle g}$ ${\displaystyle \Pi _{g}}$ ${\displaystyle g}$

(1) is a group , ${\displaystyle \Pi _{g}}$

(2) operates on the point set of 3-fold transitive , i.e. H. for every two triples of points there is a projective mapping that maps one triplet onto the other. ${\displaystyle \Pi _{g}}$ ${\displaystyle g}$

The sentence shows the meaning of the projective images

(3) A projective plane is pappusian if and only if a projective mapping of a straight line that has 3 fixed points can only be the identity. It follows that even sharp is transitive. ${\displaystyle g}$ ${\displaystyle \Pi _{g}}$

The following also applies:

(4) In a pappus projective plane over a body is isomorphic to . ${\displaystyle K}$ ${\displaystyle \Pi _{g}}$ ${\displaystyle PGL(2,K)}$

perspective tufts of straight lines

Due to the duality principle, there are also perspective / projective mappings from one straight line to another:

If two points are on a projective plane and a straight line that does not go through the two points, then the mapping that maps (projects) a straight line of the straight line in onto the straight line is called a perspective image of the straight line in onto the straight line in with axis . Executing several such images one after the other is called a projective image of one tuft onto the other. ${\displaystyle U,V}$ ${\displaystyle a}$ ${\displaystyle g}$ ${\displaystyle U}$ ${\displaystyle \pi (g)={\overline {V(g\cap a)}}}$ ${\displaystyle U}$ ${\displaystyle V}$ ${\displaystyle a}$

The statements (1) - (4) apply in an analogous manner to projective mappings of straight line tufts.

A projective mapping of one bundle of lines onto another plays an essential role in Steiner's definition of a projective conic section (see Steiner's theorem ).

Finite projective planes / spaces

The smallest projective plane consists of 7 points. It can be represented over the smallest body (with two elements).

If one assumes that the set of points (and thus also the set of lines) is finite, one gets a finite projective plane / space . Simple examples are the projective planes over finite bodies . Since there are no real finite oblique bodies ( Wedderburn's theorem ), every finite Desarguean plane or space can already be coordinated over a body.

For a finite projective plane :

If a straight line contains points, then all straight lines contain points, straight lines pass through each point and, in total, there are straight lines and points. ${\displaystyle n+1}$ ${\displaystyle n+1}$ ${\displaystyle n+1}$ ${\displaystyle n^{2}+n+1}$ ${\displaystyle n^{2}+n+1}$

${\displaystyle n}$in this case is called the order of the finite plane.

Finite projective planes also play a role in combinatorial geometry as examples of block plans .

Fano axiom

There are (axiomatic) affine planes in which the diagonals in a parallelogram do not intersect, which contradicts our experience from the real plane. To prevent this, one excludes such cases with the affine Fano axiom. For projective planes this is done by the projective Fano axiom . It is said:

(F): The points of intersection of the opposite sides (diagonal points) in any complete quadrilateral are not collinear .

If one restricts a projective plane that satisfies the Fano axiom, an affine plane arises in which the diagonals of a parallelogram are never parallel. The minimal model is not a Fano level. If a straight line is removed from the minimal model, parallelograms are created whose diagonals are parallel.

Pappus Fano planes are those that overlie a body of the characteristic , i.e. H. , can be described. ${\displaystyle \neq 2}$ ${\displaystyle 1+1\neq 0}$

Oval, ovoid, square sets

To define an oval

In addition to straight lines and planes, ovals play a role in projective planes and ovoids as the next simple curves and surfaces play a role in projective spaces .

An oval in a projective plane is a set of points that is intersected by a straight line in at most two points and there is exactly one tangent (straight line with one point of intersection) at each point.

Simple examples of ovals are the na projective conic sections. While na projective conic sections only exist in pappus planes, there are ovals in almost every projective plane. The conic sections are characterized by closure sentences (Pascal, Brianchon) and a particularly large number of symmetries (see above).

In the real projective plane, one obtains ovals that are not conic sections by combining a semicircle and a suitable half-ellipse. The curve with the equation is also an oval that is not a conic section. ${\displaystyle x^{4}+y^{4}=1}$

For finite projective planes (i.e. the set of points and set of lines are finite)

In a projective plane of order (i.e. every straight line contains points), a set is an oval if and only if is and no three points are collinear (on a straight line). ${\displaystyle n}$ ${\displaystyle n+1}$ ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle |{\mathfrak {o}}|=n+1}$ ${\displaystyle {\mathfrak {o}}}$

If the level is pappussch and odd order, the following even applies:

( Segre's Theorem ) In a finite Pappus plane of odd order, each oval is a projective conic section.

In a Pappusian plane of even order, this sentence is wrong in its generality. There are ovals that are not conic sections.

The spatial analog of an oval is the ovoid:

To define an ovoid

An ovoid in a projective space is a set of points that is intersected by a straight line in at most two points and the set of tangents through a point cover exactly one hyperplane.

Simple examples of ovoids in real projective space are ellipsoids. If you put a hemisphere and a hemi-ellipsoid together, you get an example that is not a quadric.

For finite projective spaces of dimension , the space above a body can be coordinated and the following applies: ${\displaystyle d\geq 3}$

If an ovoid is in a finite projective space of dimension , then is ${\displaystyle {\mathcal {O}}}$ ${\displaystyle d\geq 3}$ ${\displaystyle {\color {red}d=3}\;.}$

(So ​​in the finite case there are ovaries only in 3-dimensional space!)

In a projective space of order and dimension , a set of points is an ovoid if and only if is and no three points are collinear (on a straight line). ${\displaystyle n>2}$ ${\displaystyle d={\color {red}3}}$ ${\displaystyle {\mathcal {O}}}$ ${\displaystyle |{\mathcal {O}}|=n^{2}+1}$ ${\displaystyle {\mathcal {O}}}$

A consequence of Segre's theorem is:

In the 3-dimensional space of odd order , every ovoid is already a quadric.

As in the case above, this theorem is wrong for spaces of even order. In the straight case, there are ovoids ( Tits-Suzuki-Ovoids ) that are not quadrics.

Quadratic sets n are even more general. They have the same intersection behavior with straight lines as quadrics, but do not have to be. Simple examples of this are the cone and the single-shell hyperboloid. But there are also quadratic sets that are not quadrics.

Topological projective planes

A topological projective level is a projective level on whose point and line set a topology is explained in such a way that the formation of the intersection of two lines and the formation of the connecting lines are continuous operations.

Projective algebraic geometry

Instead of working in affine space , one often moves to projective space in algebraic geometry . The main advantage is that the number of intersections of two varieties can then easily be determined with the help of Bézout's theorem . ${\displaystyle K^{n}}$

Projective space as an association

A projective space and its subspaces can also be understood as a special association :

The lattice of the subspaces of a finite dimensional projective space is equivalent to a finite dimensional complemented atomic modular lattice .

literature

• E. Artin : Geometric Algebra , Interscience Publishers, 1957
• F. Bachmann : Structure of geometry from the reflection concept , 1959, (2nd edition. Springer 1973)
• R. Baer : Linear Algebra and Projective Geometry , (first edition: 1952), Dover, 2005, ISBN 978-0-486-44565-6
• W. Blaschke : Projective Geometry , Springer-Verlag, 2013, ISBN 3-0348-6932-0
• Albrecht Beutelspacher : Introduction to Finite Geometry . I. Block plans. BI Wissenschaftsverlag, Mannheim / Vienna / Zurich 1982, ISBN 3-411-01632-9 .
• A. Beutelspacher, U. Rosenbaum: Projective geometry Vieweg + Teubner, Braunschweig et al. 1992, ISBN 3-528-07241-5
• H. Brauner : Geometry of projective spaces I, II , BI-Verlag, 1976
• Harold SM Coxeter : Projective Geometry , Springer 2003,
• P. Dembowski : Finite Geometries , Springer-Verlag, 1968, ISBN 978-3-642-62012-6
• Gerd Fischer : Analytical Geometry . Vieweg 1978, pp. 131-204
• R. Hartshorne: Foundations of Projective Geometry , New York: WA Benjamin, Inc, 1967
• David Hilbert : Fundamentals of Geometry . 14th edition. Teubner, Stuttgart 1999, ISBN 3-519-00237-X ( archive.org - first edition: 1899).
• JWP Hirschfeld: Projective Geometries Over Finite Fields , Oxford University Press, 1979, ISBN 978-0-19-850295-1
• DR Hughes, FC Piper: Projective Planes , Springer-Verlag, 1973, ISBN 0-387-90043-8 .
• L. Kadison, MT Kromann: Projective Geometry and modern Algebra , Birkhäuser-Verlag, 1996
• Gerhard Kowol: Projective Geometry and Cayley-Klein Geometries of the Plane . Birkhäuser, Boston 2009
• Derrick Norman Lehmer: An Elementary Course in Synthetic Projective Geometry. Gutenberg eText
• H. Karzel , K. Sörensen, D. Windelberg Introduction to Geometry , Vandenhoeck and Ruprecht 1973
• H. Lenz : Lectures on projective geometry , Geest and Portig, Leipzig 1965.
• Rolf Lingenberg : Fundamentals of Geometry , BI-Taschenbuch, 1969.
• Günter Pickert : Projective levels . 2nd Edition. Springer, Berlin / Heidelberg / New York 1975, ISBN 3-540-07280-2 .
• Jürgen Richter-Gebert : Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry . Springer Science & Business Media, 2011, ISBN 978-3-642-17285-4 .
• Pierre Samuel : Projective Geometry , Springer-Verlag 1988, ISBN 978-0-387-96752-3

Web links

• Projective Geometry. ( Memento of May 4, 2005 in the Internet Archive ) (PDF)
• Hanns-Jörg Stoss: Projective Geometry I.
• Projective geometry , short script. (PDF) University of Darmstadt
• Nigel Hitchin: Projective Geometry.

Individual evidence

1. ↑ Beutelspacher / Rosenbaum: p. 162
2. ↑ R. Lingenberg: Fundamentals of Geometry , p. 70
3. ↑ H. Lenz: Lectures on projective geometry , Akad. Verl.-Gesellsch., 1965, p. 29
4. ^ H. Brauner: Geometry of projective spaces I , BI-Verlag, 1976, pp. 42-47
5. ^ R. Lingenberg: Fundamentals of Geometry , BI-Verlag, 1978, p. 113
6. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 28
7. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 48
8. ^ P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 48
9. ^ O. Tamaschke: Projektive Geometrie I , BI-Taschenbuch, 1969, p. 151