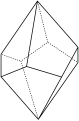
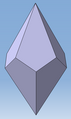
Trapezoid
A trapezoid is a polyhedron that is bounded by congruent "crooked" squares - that is, by those where neither side of another is parallel ( trapezoids or trapezoids in the older sense). A trapezoid can be thought of as a bipyramid in which the upper pyramid is twisted against the lower pyramid by any angle. A trapezoid is called n-gonal , where n is half the number of its faces. (Two touching edges of the rectangles are necessarily the same length.)
Trapezohedra occur in nature as a crystal form : They are the general planar form of the enantiomorphic crystal classes 32 (trigonal-trapezoidal), 422 (tetragonal-trapezoidal) and 622 (hexagonal-trapezoidal class).
symmetry
Trapezohedra are point-symmetrical . The point of symmetry is the intersection of the space diagonals . One of the room diagonals represents an n-fold axis of rotation.
Trapezohedron with higher symmetry
A trapezoid with higher symmetry is created when the surfaces of the upper pyramid are exactly in the middle between those of the lower pyramid. The angle of rotation is then 180 ° / m for an m-fold pyramid. The surfaces of such bodies are dragon squares ("deltoids"). These higher symmetrical trapezoids are also called deltoahedra or antipyramids ; their dual polyhedra are straight antiprisms .
trigonal trapezoid
tetragonal trapezoid
Pentagonal trapezoid as a ten-sided dice
hexagonal trapezoid
Deltoidal icositetrahedron
In addition, the cubic Deltoidalikositetrahedron , a body with 24 kite-shaped surfaces, is sometimes called a trapezoid.
Individual evidence
- ^ Brockhaus' Kleines Konversations-Lexikon. 5th edition 1911, article "Trapez"
Web links
- Eric W. Weisstein : Trapezohedron . In: MathWorld (English).