Trembling-hand-perfect balance

The trembling-hand-perfect balance or perfect balance of the trembling hand represents a possibility of selecting Nash equilibria . It was developed by Reinhard Selten , who wrote the idea in 1975 under the name "A Model of Slight Mistakes" in the "International Journal of Game Theory "published. The aim is to determine how vulnerable a balance is to a player's mistakes. After seldom there are no mistakes when the players act absolutely rationally. In reality, however, you have to expect wrong decisions by your opponent. To represent this in game theory, the trembling-hand-perfect balance was developed.

Simple illustration of the approach

Reinhard Selten (2001)

Put simply, the idea of trembling-hand-perfect balance means : Suppose player A assumes that player B always plays the strategy and player A's best answer to that is his strategy . Then is always strategy will still play the best choice if Player B accidentally, ie with a low probability of error , plays? Under these circumstances , if Player A's best strategy is still, it is a trembling hand perfect strategy . ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle (\epsilon )}$ ${\displaystyle {\begin{aligned}b_{2}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$

Trembling-hand-perfect balance in normal form games

Through the following normal form game , the approach of trembling-hand-perfect equilibrium is illustrated very simply using the following payout matrix:

Player A / Player B	( ) ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$	( ) ${\displaystyle {\begin{aligned}b_{2}\end{aligned}}}$
( ) ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$	(3, 3)	(5, 0)
( ) ${\displaystyle {\begin{aligned}a_{2}\end{aligned}}}$	(-2, -2)	(5, 0)

The two Nash equilibria are in this example at and . Now it should be determined whether one of the two equilibria (or both) are trembling-hand-perfect equilibria . Suppose player A wants to play his strategy and assumes that player B will play his strategy , since both would then get a payout of 3. However, player A is not entirely sure whether player B is not playing his strategy with a low probability of error . In order to find out whether, despite this error probability from player B, the best choice of player A and thus trembling-hand-perfect , the following must be checked: The expected payout of player A, if he chooses, must be at least as large as the expected one Payout for choosing from . ${\displaystyle {\begin{aligned}(a_{1},b_{1})\end{aligned}}}$ ${\displaystyle {\begin{aligned}(a_{2},b_{2})\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}b_{2}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{2}\end{aligned}}}$

${\displaystyle (\epsilon )}$be the error probability of player B, which is assumed to be very small. That is, is the associated counter-probability. With ${\displaystyle (1-\epsilon )}$ ${\displaystyle 0<(\epsilon )<<1}$

So Player A's expected payout for choosing is: ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$

${\displaystyle \mathrm {E} [u(a_{1})]=(1-\epsilon )[u(a_{1},b_{1})]+(\epsilon )[u(a_{1},b_{2})]}$

= + ${\displaystyle (1-\epsilon )\cdot 3}$ ${\displaystyle (\epsilon )\cdot 5}$

In comparison, the expected payout of the strategy : ${\displaystyle {\begin{aligned}a_{2}\end{aligned}}}$

${\displaystyle \mathrm {E} [u(a_{2})]=(1-\epsilon )[u(a_{2},b_{1})]+(\epsilon )[u(a_{2},b_{2})]}$

= + ${\displaystyle (1-\epsilon )\cdot (-2)}$ ${\displaystyle (\epsilon )\cdot 5}$

It is easy to see that:

${\displaystyle (1-\epsilon )\cdot 3}$+ > + ${\displaystyle (\epsilon )\cdot 5}$ ${\displaystyle (1-\epsilon )\cdot (-2)}$ ${\displaystyle (\epsilon )\cdot 5}$

Even if player B plays with a low chance of making a mistake , player A is the best possible choice. So the strategy is trembling-hand-perfect . A trembling-hand-perfect balance , however, consists of a combination of two trembling-hand-perfect strategies. So in order to check whether the strategy combination is such, player B must also test it. Analogous to the strategy, it looks like this: ${\displaystyle {\begin{aligned}b_{2}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}(a_{1},b_{1})\end{aligned}}}$ ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$

Player B's expected payout for choosing is: ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$

${\displaystyle \mathrm {E} [u(b_{1})]=(1-\epsilon )[u(a_{1},b_{1})]+(\epsilon )[u(a_{2},b_{1})]}$

= + ${\displaystyle (1-\epsilon )\cdot 3}$ ${\displaystyle (\epsilon )\cdot (-2)}$

In comparison, the expected payout of the strategy : ${\displaystyle {\begin{aligned}b_{2}\end{aligned}}}$

${\displaystyle \mathrm {E} [u(b_{2})]=(1-\epsilon )[u(a_{1},b_{2})]+(\epsilon )[u(a_{2},b_{2})]}$

= + ${\displaystyle (1-\epsilon )\cdot 0}$ ${\displaystyle (\epsilon )\cdot 0}$

And again it can be clearly seen that:

${\displaystyle 0<(1-\epsilon )\cdot 3+(\epsilon )\cdot (-2)=3-(5\cdot \epsilon )}$

This means that the strategy trembling-hand-perfect and the Nash equilibrium is a trembling-hand-perfect balance . ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}(a_{1},b_{1})\end{aligned}}}$

Formal definition using a perturbated game

Simple definition of a perturbated game

A perturbated game is a copy of the underlying game, with the restriction that every player must play all pure strategies with a positive probability . That is, in normal game player A is able to play his strategies . In the perturbated game must be. ${\displaystyle 0\leq \epsilon _{a}\leq 1}$ ${\displaystyle \epsilon >0}$

Formal definition

The starting point is a game in strategic form:

${\displaystyle {\begin{aligned}G=(I,(M_{i}),(P_{i}))\end{aligned}}}$, and ${\displaystyle {\begin{aligned}(i\in I)\end{aligned}}}$

Where the number of players represents the set of mixed strategies, which is based on the possible distribution of the pure strategies and is the expected payout of players . The central idea, in order to map possible errors of the players, is to assume that no pure strategy with a probability of zero can be played. In such a perturbed game: ${\displaystyle {\begin{aligned}I\end{aligned}}}$ ${\displaystyle {\begin{aligned}M_{i}\end{aligned}}}$ ${\displaystyle {\begin{aligned}S_{i}\end{aligned}}}$ ${\displaystyle {\begin{aligned}P_{i}\end{aligned}}}$ ${\displaystyle {\begin{aligned}i\end{aligned}}}$

For any player with pure strategies, is the set of positive probabilities for which: ${\displaystyle {\begin{aligned}(i\in I)\end{aligned}}}$ ${\displaystyle {\begin{aligned}n_{i}\end{aligned}}}$ ${\displaystyle {\begin{aligned}\epsilon _{i}=(\epsilon _{i}^{1},\epsilon _{i}^{2},...,\epsilon _{i}^{n})\end{aligned}}}$

${\displaystyle {\begin{aligned}\epsilon _{i}\gg 0\end{aligned}}}$and . ${\displaystyle \sum \nolimits _{j=1}^{n_{i}}\epsilon _{i}^{j}<1}$

So the amount of mixed strategies in the perturbed game is:

${\displaystyle {\begin{aligned}M_{i}^{\epsilon }=(m_{i}\in {M_{i}}|m_{i}^{k}\geq \epsilon _{i}^{k})\end{aligned}}}$, for . ${\displaystyle {\begin{aligned}k=(1...n_{i})\end{aligned}}}$

This means that players , each of his pure strategies the number , at least with the probability to play. From this follows the perturbated game: ${\displaystyle {\begin{aligned}i\end{aligned}}}$ ${\displaystyle {\begin{aligned}(i\in I)\end{aligned}}}$ ${\displaystyle {\begin{aligned}k\end{aligned}}}$ ${\displaystyle {\begin{aligned}\epsilon _{i}^{k}\end{aligned}}}$

${\displaystyle {\begin{aligned}G(\epsilon )=(I,(M_{i}^{\epsilon }),(P_{i}))\end{aligned}}}$, and ${\displaystyle {\begin{aligned}(i\in I)\end{aligned}}}$

A Nash equilibrium in the game was perturbed and be a Nash equilibrium in the main game: . If you let the probability of error in the perturbated game go to zero and thereby the equilibrium of the perturbated game becomes the same as in normal game, one speaks of a trembling-hand-perfect balance . In formal terms, this means if ${\displaystyle {\begin{aligned}m^{*}(\epsilon )\end{aligned}}}$ ${\displaystyle {\begin{aligned}m^{*}\end{aligned}}}$ ${\displaystyle {\begin{aligned}\epsilon \end{aligned}}}$

${\displaystyle {\begin{aligned}\lim _{\epsilon \to 0}m^{*}(\epsilon )=m^{*}\end{aligned}}}$,

it is a trembling-hand-perfect balance .

example

The starting game is a normal form game with the following payout matrix:

Player A / Player B	( ) ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$	( ) ${\displaystyle {\begin{aligned}b_{2}\end{aligned}}}$
( ) ${\displaystyle {\begin{aligned}a_{1}\end{aligned}}}$	(3, 3)	(0, 0)
( ) ${\displaystyle {\begin{aligned}a_{2}\end{aligned}}}$	(0, 0)	(0, 0)

In the normal game there are two Nash equilibria , which result from the strategy combinations and . For the two players, when choosing their best answer, it depends on which strategy the respective opponent chooses. ${\displaystyle {\begin{aligned}(a_{1}/b_{1})\end{aligned}}}$ ${\displaystyle {\begin{aligned}(a_{2}/b_{2})\end{aligned}}}$

This is not the case in the perturbated game. Because if there is even a tiny chance that player B will choose his strategy , then player A's best answer to it is to play. Since this probability exists in the perturbed game by definition, player A would always play. But player A also has to play his strategy with a positive probability in the perturbed game . So his best answer is to play the mixed strategy - the lowest possible chance for . ${\displaystyle {\begin{aligned}b_{1}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}=1\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{1}=1\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{2}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{2}=a_{2}^{min}\end{aligned}}}$ ${\displaystyle {\begin{aligned}a_{2}\end{aligned}}}$

Because of the symmetry of the game, the best strategy for player B is accordingly: ${\displaystyle {\begin{aligned}b_{2}=b_{2}^{min}\end{aligned}}}$

So the equilibrium in the perturbated game is:

${\displaystyle {\begin{aligned}(1-a_{2}^{min},a_{2}^{min}),(1-b_{2}^{min},b_{2}^{min})\end{aligned}}}$

If you let go now and against , then the perturbed game almost becomes normal again, because: ${\displaystyle {\begin{aligned}a_{2}^{min}\end{aligned}}}$ ${\displaystyle {\begin{aligned}b_{2}^{min}\end{aligned}}}$ ${\displaystyle {\begin{aligned}0\end{aligned}}}$

${\displaystyle \lim _{a_{2}^{min},b_{2}^{min}\to 0}[(1-a_{2}^{min},a_{2}^{min}),(1-b_{2}^{min},b_{2}^{min})]=[(1,0),(1,0)]=(a_{1},b_{1})}$

If the error probability is allowed to approach zero and the equilibrium of the perturbed game is thereby moved towards a Nash equilibrium of the underlying game, then this equilibrium is a trembling-hand-perfect one .

In this example, the perturbated game moves against balance and is therefore trembling-hand-perfect . ${\displaystyle {\begin{aligned}(a_{1}/b_{1})\end{aligned}}}$

${\displaystyle {\begin{aligned}(1-a_{2}^{min},a_{2}^{min}),(1-b_{2}^{min},b_{2}^{min})\end{aligned}}}$

Trembling-hand-perfect balance in sequential games

The concept of trembling-hand-perfect balance can also be used for sequential games . Similar to the normal form games , it is useful here for the selection of subgame-perfect equilibria in order to determine whether such an equilibrium persists even with a low error probability.

example

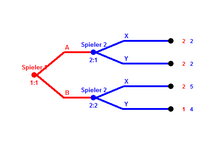
Game tree of an extensive form game between two players

In the on the right there are four subgame perfect equilibria :

${\displaystyle {\begin{aligned}(A,(X|A,X|B))\end{aligned}}}$, so player 1 plays his strategy and player 2 plays in the event that player 1 has chosen and also in the event that player 1 has chosen. are the other three subgame-perfect equilibria. ${\displaystyle {\begin{aligned}A\end{aligned}}}$ ${\displaystyle {\begin{aligned}X\end{aligned}}}$ ${\displaystyle {\begin{aligned}A\end{aligned}}}$ ${\displaystyle {\begin{aligned}X\end{aligned}}}$ ${\displaystyle {\begin{aligned}B\end{aligned}}}$ ${\displaystyle {\begin{aligned}(A,(Y|A,X|B)),(B,(X|A,X|B)),(B,(Y|A,X|B))\end{aligned}}}$

However, only the two equilibria in which Player 1 chooses his strategy are trembling-hand-perfect . Because even if there is only a tiny probability that player 2 will play his strategy , it is better for player 1 to always play, as he always gets a payout of 2 and he can never do better with the strategy than with that Strategy . ${\displaystyle {\begin{aligned}A\end{aligned}}}$ ${\displaystyle {\begin{aligned}Y\end{aligned}}}$ ${\displaystyle {\begin{aligned}A\end{aligned}}}$ ${\displaystyle {\begin{aligned}B\end{aligned}}}$ ${\displaystyle {\begin{aligned}A\end{aligned}}}$

The two Trembling-hand perfect equilibria are therefore: . ${\displaystyle {\begin{aligned}(A,(X|A,X|B)),(A,(Y|A,X|B))\end{aligned}}}$

Trembling-hand-perfect balance in extensive games with the agent normal form

Elon Kohlberg's Dalekspiel in extensive form

The Dalek game developed by the game theorist Elon Kohlberg, and here slightly modified, is an example of another application of the trembling-hand-perfect balance . The agent normal form developed by Harold W. Kuhn in 1953 is used to compensate for the loss of information when an extensive game is reduced to the normal form . As can be seen in the Dalek game on the right, player 1 is split into two agents in order to be able to mathematically map uncorrelated decisions at each decision node.

Player 1 / Player 2	(L)	(R)
(gl)	(2, 5)	(2, 5)
(gr)	(2, 5)	(2, 5)
(ul)	(4, 1)	(0, 0)
(ur)	(0, 0)	(1, 4)

In the normal form one can easily recognize that there are three Nash equilibria in pure strategies are: . In order to examine these equilibria for their trembling hand perfectness, one has to ensure that the error probabilities that player 1 has at his two decision nodes do not correlate with one another. This means that an error at the first decision node must not lead to an increase or decrease in the probability of a further error. To ensure this, as already described above, player 1 is divided into two agents who make their decisions independently of one another. ${\displaystyle {\begin{aligned}(gl,R),(gr,R),(ul,L)\end{aligned}}}$

Now we assume that the first agent (Sp1A) has a low probability of making a mistake and playing instead of . ${\displaystyle \epsilon }$ ${\displaystyle {\begin{aligned}u\end{aligned}}}$ ${\displaystyle {\begin{aligned}g\end{aligned}}}$

Accordingly, the second agent (Sp1B) has a probability of making a mistake and playing instead of . ${\displaystyle {\begin{aligned}\delta \end{aligned}}}$ ${\displaystyle {\begin{aligned}l\end{aligned}}}$ ${\displaystyle {\begin{aligned}r\end{aligned}}}$

Player 2 will eventually make a mistake and play instead of . ${\displaystyle {\begin{aligned}\lambda \end{aligned}}}$ ${\displaystyle {\begin{aligned}L\end{aligned}}}$ ${\displaystyle {\begin{aligned}R\end{aligned}}}$

With the entered probabilities, the normal form looks like this from above:

Player 1 / Player 2	(L)	(R)	probability
(gl)	(2, 5)	(2, 5)	${\displaystyle (1-\epsilon )\cdot \delta }$
(gr)	(2, 5)	(2, 5)	${\displaystyle (1-\epsilon )\cdot (1-\delta )}$
(ul)	(4, 1)	(0, 0)	${\displaystyle \epsilon \cdot \delta }$
(ur)	(0, 0)	(1, 4)	${\displaystyle \epsilon \cdot (1-\delta )}$
probability	${\displaystyle {\begin{aligned}\lambda \end{aligned}}}$	${\displaystyle {\begin{aligned}(1-\lambda )\end{aligned}}}$

Now it is easy to see that the strategies and for player 1 for small trembling are hand-perfect strategies . Because he receives a safe payout of 2 no matter how player 2 decides. With the only better payout of 4 when choosing , he receives the payout based on the probabilities in the expected value: ${\displaystyle {\begin{aligned}(gr)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(gl)\end{aligned}}}$ ${\displaystyle {\begin{aligned}\lambda \end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul)\end{aligned}}}$

${\displaystyle {\begin{aligned}\mathrm {E} [u(ul)]=(1-\lambda )\cdot 0+(\lambda )\cdot 4\end{aligned}}}$and for this expected value is worse than for and . ${\displaystyle {\begin{aligned}\lambda >0,5\end{aligned}}}$ ${\displaystyle {\begin{aligned}(gr)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(gl)\end{aligned}}}$

For player 2 too, the strategy is trembling-hand-perfect because the only strategy combination where player 2 gets a bigger payout for than for is as opposed to . But since only occurs when both agents of player 1 make a mistake, has the lowest probability ( ). ${\displaystyle {\begin{aligned}(R)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(L)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(R)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul,L)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul,R)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul)\end{aligned}}}$ ${\displaystyle \epsilon \cdot \delta }$

With that the two equilibria and trembling-hand-perfect . Balance isn't because the strategy , as just shown, is not a trembling-hand-perfect strategy . ${\displaystyle {\begin{aligned}(gr,R)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(gl,R)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul,L)\end{aligned}}}$ ${\displaystyle {\begin{aligned}(ul)\end{aligned}}}$

See also

• Reinhard Rare
• Game theory
• Nash equilibrium
• Partial perfect balance
• Normal form (game theory)

literature

• Reinhard Selten: A reexamination of the perfectness concept for equilibrium points in extensive games, in: International Journal of Game Theory . Physica-Verlag, Vienna 1975, p. 25-55 .
• Harold William Kuhn: Extensive Games and the Problem of Informations, in: Contribution to the Theory of Games, Vol. 2 . Princeton Univ. Press, Princeton 1953, pp. 193-216 .
• Elon Kohlberg, Jean-Francois Mertens: On the Strategic Stability of Equilibria . Econometrica, 1986, pp. 1003-1037 .
• Robert Gibbons: A Primer in Game Theory . Financial Times, Harlow 1992.
• Thomas Riechmann: Game Theory . 3. Edition. Vahlen, Munich 2010.
• Christian Rieck: Game Theory . 8th edition. Rieck, Eschborn 2008.
• Alexander Mehlmann: Strategic Games for Beginners . Friedr. Vieweg & Sohn Verlag, Wiesbaden 2007.
• Ken Binmore: Fun and Games . 1st edition. Heath, Lexington 1992.
• Jürgen Eichberger: Game Theory for Economists . 1st edition. Emerald, Bingley 2007.

Web links

• Project of the University of Munich, as an encyclopedia on game theory

Individual evidence

1. ^ Walter Schlee: Introduction to Game Theory: With Examples and Exercises, p. 289
2. ↑ Reinhard Selten: A reexamination of the perfectness concept for equilibrium points in extensive games, in: International Journal of Game Theory . Physica-Verlag, Vienna 1975, p. 25-55 . P. 35
3. ↑ Thomas Riechmann: Game Theory . 3. Edition. Vahlen, Munich 2010. pp. 38-40
4. ↑ Jürgen Eichberger: Game Theory for Economists . 1st edition. Emerald, Bingley 2007. pp. 111-113
5. ↑ Thomas Riechmann: Game Theory . 3. Edition. Vahlen, Munich 2010. pp. 94-95
6. ↑ Thomas Riechmann: Game Theory . 3. Edition. Vahlen, Munich 2010. p. 53
7. ^ Harold William Kuhn: Extensive Games and the Problem of Informations, in: Contribution to the Theory of Games, Vol. 2 . Princeton Univ. Press, Princeton 1953, pp. 193-216 .
8. ↑ Alexander Mehlmann: Strategic Games for Beginners . Friedr. Vieweg & Sohn Verlag, Wiesbaden 2007. pp. 88–92
9. ↑ Ken Binmore: Fun and Games . 1st edition. Heath, Lexington 1992. pp. 454-462