Chen notation

The Chen notation is a graphical notation for entity-relationship models . It is named after the computer scientist Peter Chen , who introduced it together with the entity relationship model in 1976 to represent data models .

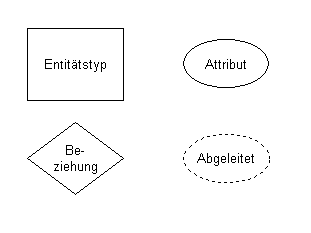
The representations

The

Attributes

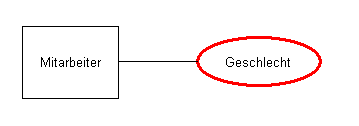
An attribute

describes a property of an entity type
has a unique name
is time invariant

In Chen's original draft, no separate notation is provided for attributes.

Simple attributes

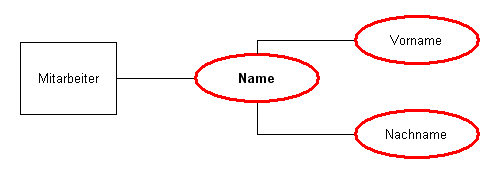
Compound attributes

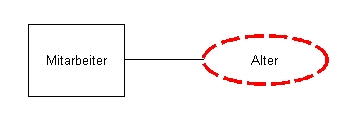
Derived / Computed Attributes

In this case, the age is calculated based on the date of birth, for example.

Relationships

Relationship types are logical links between two or more entity types.

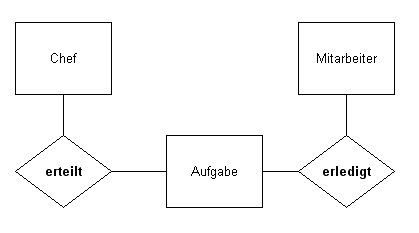
Binary relationship types

Boss gives task
Employee does the job

Ternary relationship types

Boss and employees attend further training

Attributes of a relationship

Cardinalities

To represent the cardinalities of binary relationship types, the number 1 , in the sense of 0 or 1 , and the letters m and n , in the sense of 0 to ∞, are used.

1: 1 ([0 or 1] to [1 or 0])

Each entity from the first entity set can be related to at most one entity from the second entity set, and vice versa.

1: n ([0 or 1] to any number)

Each entity from the first entity set can be related to any number of entities from the second entity set. Each entity from the second entity set can be related to at most one entity from the first entity set.

m: n (any number to any number)

Each entity from the first entity set can be related to any number of entities from the second entity set, and vice versa.

Modified Chen notation (MC notation)

The Modified Chen Notation ( Modified Chen Notation , MC Notation ) is an extension of the Chen notation, in which the statement "no or one element" with the letter c ( choice , can ), and the statement "one or more elements (e) "is indicated with the letter m ( must , multiple ). Therefore, MC is sometimes interpreted as a must- can.

1: 1 (1 to 1)

Each entity of the first entity set is related to exactly one entity of the second entity set, and vice versa.

1: c (1 to [0 or 1])

Each entity of the first entity set can be related to at most one entity of the second entity set. Each entity of the second entity set is related to exactly one entity of the first entity set.

1: m (1 to [at least 1])

Each entity of the first entity set is related to at least one entity of the second entity set. Each entity of the second entity set is related to exactly one entity of the first entity set.

1: mc (1 to [any number])

Each entity of the first entity set can be related to any number of entities of the second entity set. Each entity of the second entity set is related to exactly one entity of the first entity set.

c: c ([1 or 0] to [0 or 1]; corresponds to 1: 1 in Chen notation)

Each entity of the first entity set can be related to at most one entity of the second entity set, and vice versa.

c: m ([0 or 1] to [at least 1])

Each entity of the first entity set is related to at least one entity of the second entity set. Each entity of the second entity set can be related to at most one entity of the first entity set.

c: mc ([0 or 1] to [any number]; corresponds to 1: n in Chen notation)

Each entity of the first entity set can be related to any number of entities of the second entity set. Each entity of the second entity set can be related to at most one entity of the first entity set.

m: m ([at least 1] to [at least 1])

Each entity of the first entity set is related to at least one entity of the second entity set, and vice versa.

m: mc ([at least 1] to [any number])

Each entity of the first entity set can be related to any number of entities of the second entity set. Each entity of the second entity set is related to at least one entity of the first entity set.

mc: mc ([any number] to [any number]; corresponds to m: n in Chen notation)

Each entity in the first entity set can be related to any number of entities in the second entity set, and vice versa.

roll

The entities participating in a relationship can be referred to with roles.

literature

Peter Pin-Shan Chen: The Entity-Relationship Model - Toward a Unified View of Data . In: ACM Transactions on Database Systems , Vol 1, No 1, March 1976 - The original article (English, PDF ; 1.7 MB)