Pulse oscillometry

The impulse oscillometry is a process for the mechanical analysis of the respiratory ( lung function testing ) and is used in particular for the determination of airway resistance . In addition to airway resistance, it also records the inertia and elasticity resistance of the lungs and thorax . The results can be used to diagnose respiratory diseases.

history

Based on the principles of oscillometry , E. Müller and J. Vogel developed a measuring method whose pneumatic excitation varied. The frequency mixture applied to the patient was generated with the help of a pressure pulse. The advantage over other excitation signals lies in the signal duration of a few seconds and the simple technical implementation with the aid of a loudspeaker.

Measuring equipment

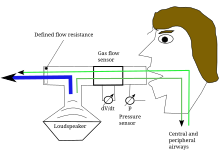
A sensor that can measure pressure and flow at the same time is located near the patient. This breathes through the sensor via a mouthpiece, at the end of which there is a loudspeaker and a defined terminating resistor. Already technically implemented measuring devices usually use a loudspeaker as a pulse generator. The patient breathes through the sensor and a metal screen as a defined terminating resistor.

Measurement method

An exemplary structure of a measuring system

The patient breathes at rest through a mechanical structure, at the proximal end of which a defined flow resistance inhibits breathing. A pneumatic pulse is coupled into this breathing channel. Most of the energy in the pulse is lost at the distal end of the apparatus. Another part, which depends on the airway resistance, is given to the patient. Due to the resistive and inertive components of the patient's airway impedance, pressure builds up in the vicinity of the mouthpiece. The associated flow impulse can also be measured and is superimposed on the breathing air flow. ${\displaystyle p(t)}$ ${\displaystyle {\dot {V}}(t)}$

Pressure and flow are recorded by the sensor, which is placed near the patient. The measured value processing is carried out on the basis of several pulses. Due to the normal breathing of the patient, pressure and flow signals are composed of the applied pulse shape and a sinusoidal oscillation of the breathing rate. The individual impulses are extracted from the measured values ​​and, with the help of a baseline correction, approximately freed from patient breathing.

The individual pulses obtained are mapped into the Fourier space with the aid of the Fourier transformation , more precisely the discrete Fourier transformation . ${\displaystyle p_{n}(t)/{\dot {V}}_{n}(t)}$

${\displaystyle P_{n}(j\omega )={\mathfrak {F}}\{p_{n}(t)\}}$

${\displaystyle V_{n}(j\omega )={\mathfrak {F}}\{{\dot {V}}_{n}(t)\}}$

The function values ​​for individual frequencies are averaged over all pulses. In this way, the artifacts of the patient's breathing that may still be contained after the baseline correction can be eliminated. ${\displaystyle \omega }$ ${\displaystyle N}$

The quotient of the complex function values ​​of the Fourier transformation of pressure and flow results in the impedance described above.

${\displaystyle Z(j\omega )={\frac {P(j\omega )}{{\dot {V}}(i\omega )}}}$

${\displaystyle R(f)={\mathfrak {Re}}\{Z(j2\pi f)\}}$

${\displaystyle X(f)={\mathfrak {Im}}\{Z(j2\pi f)\}}$

The real and imaginary parts of the impedance are used for clinical diagnosis. Plotted in two graphs over the frequencies from 5 Hz to around 35 Hz, characteristic figures can be recognized there that support a diagnosis of the lung anomaly.

Systems theory view

Known from system theory , the transfer function of an unknown system can be determined with the help of the impulse response . An infinitely high impulse with an infinitesimally small width, the Dirac impulse , is given as an input signal to the unknown system. At the output one recognizes a signal which, mapped in the Fourier space, gives the transfer function of the system to be examined.

The human respiratory tract can be thought of as an unknown system. A pressure pulse is applied to the patient's mouth. The system response is directly superimposed on the applied pulse due to the short time it takes for the pulse to travel from the lungs to the measuring apparatus.

In reality there can never be an ideal Dirac impulse and therefore the loudspeaker impulse corresponds to a strongly filtered Dirac impulse without those frequency components that the loudspeaker cannot generate.

This approach only helps to characterize the measurement process in part, but it fails because system theory can be used with decoupled individual systems and not with coupled system structures. The patient's airways directly influence the generation of impulses and the transmission via the measuring apparatus. Therefore, the theory of systems only serves for a better understanding.

swell

1. ↑ Pulse oscillometry by Johannes Vogel and Udo Smidt

This article is about a health issue. It is not used for self-diagnosis and does not replace a diagnosis by a doctor. Please note the information on health issues !