Monoidal category

In mathematics , a designated monoidal category is a category that double-digit functor and a unit object is equipped. ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \otimes \colon {\mathcal {C}}\times {\mathcal {C}}\to {\mathcal {C}}}$ ${\displaystyle I\in \left|{\mathcal {C}}\right|}$

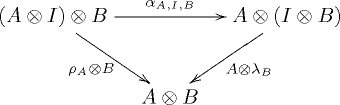
The link must be associative in the sense that there is a natural equivalence , ${\displaystyle \alpha }$

${\displaystyle \alpha _{A,B,C}\colon (A\otimes B)\otimes C\to A\otimes (B\otimes C),}$

gives; must be left and right neutral in the sense that there are natural equivalences and given by ${\displaystyle I}$ ${\displaystyle \lambda }$ ${\displaystyle \rho }$

${\displaystyle \lambda _{A}\colon I\otimes A\to A}$and . ${\displaystyle \rho _{A}\colon A\otimes I\to A}$

These natural transformations are said to be coherent. All necessary coherence conditions follow from the commutativity of the following two diagrams:

and

From these two conditions it follows that every such diagram commutes: This is Mac Lane's "coherence theorem ".

• A monoidal category can be viewed as a bi-category with one object.
• The concept of the monoid object can be defined in a monoidal category, which generalizes that of the monoid .

Examples

Any category containing finite products and an end object can be viewed as a symmetrically monoidal category: the two-digit functor is defined by a natural selection of products and the end object is the unit object. Similarly, we can choose a co- product as the two-digit functor and an initial object as the unit object .

We now show the structure of two such monoidal categories in parallel:

${\displaystyle R}$-Mod	set
For a commutative ring the category is -Mod of - modules a symmetric monoidal category with product (the tensor product ) and unity . ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle \otimes }$ ${\displaystyle R}$	The category set is symmetrical monoidal with product and unit . ${\displaystyle \times }$ ${\displaystyle \{*\}}$
A unitary associative algebra is an object of -Mod together with arrows and , for which the following diagrams commute: ${\displaystyle R}$ ${\displaystyle \nabla \colon A\otimes A\to A}$ ${\displaystyle \eta \colon R\rightarrow A}$	A monoid is an object M together with arrows and ${\displaystyle \circ \colon M\times M\rightarrow M}$ ${\displaystyle 1\colon \{*\}\to M}$, for which the following diagrams commute:
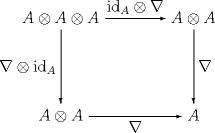
and	and
.	.
A koalgebra is an object C with arrows and , for which the following diagrams commute: ${\displaystyle \Delta \colon C\to C\otimes C}$ ${\displaystyle \varepsilon \colon C\to R}$	For each object S in the Set category, there are two clearly defined arrows and , for which the following diagrams commute: ${\displaystyle \Delta \colon S\to S\times S}$ ${\displaystyle \varepsilon \colon S\to \{*\}}$
and	and
.	.
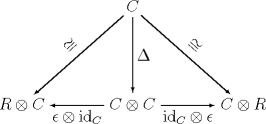	In particular it is unique because is end object . ${\displaystyle \varepsilon }$ ${\displaystyle \{*\}}$

swell

• Joyal, André; Street, Ross (1993). "Braided Tensor Categories". Advances in Mathematics 102 , 20-78.
• Mac Lane, Saunders (1997), Categories for the Working Mathematician (2nd ed.). New York: Springer-Verlag.