Wiener index

The Wiener index - named after Harry Wiener - is the oldest topological descriptor that maps the structure of a molecule in a number.

formulation

${\displaystyle W={\frac {1}{2}}\sum _{i,j}^{N}d_{ij}}$

• W: Wiener index
• N: number of non-hydrogen atoms in the structure
• d _ij : Number of bonds on the shortest path between atoms i and j

The factor ¹ / ₂ states that every path is received only once in the index.

use

The Wiener index is used in the methods of the quantitative structure-activity relationship (QSPR) to correlate substance properties such as the saturation vapor pressure with the molecular structure . Since the Wiener index does not differentiate between different atoms, it can only be used meaningfully within a homologous series .

Sample calculation

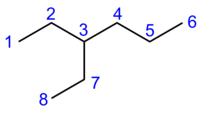
The Wiener index for 3-ethylhexane is W = 72. It is the sum of the distances

1-2 (1), 1-3 (2), 1-4 (3), 1-5 (4), 1-6 (5), 1-7 (3), 1-8 (4),

2-3 (1), 2-4 (2), 2-5 (3), 2-6 (4), 2-7 (2), 2-8 (3),

3-4 (1), 3-5 (2), 3-6 (3), 3-7 (1), 3-8 (2),

4-5 (1), 4-6 (2), 4-7 (2), 4-8 (3),

5-6 (1), 5-7 (3), 5-8 (4),

6-7 (4), 6-8 (5),

7-8 (1)

→ 1 + 2 + 3 + 4 + 5 + 3 + 4 + 1 + 2 + 3 + 4 + 2 + 3 + 1 + 2 + 3 + 1 + 2 + 1 + 2 + 2 + 3 + 1 + 3 + 4 + 4 + 5 +1 = 72.

Sample values

material	Wiener index
n-hexane	35
2-methylpentane	32
3-methylpentane	31
2,3-dimethylbutane	29

These four examples with the identical empirical formula (C ₆ H ₁₄ ) make it clear that the Wiener index is highest without branching and that it becomes smaller with increasing branching in the molecular structure; with the same number of branches, it becomes smaller with increasing molecular symmetry .

Calculation of the maximum values ​​for W

The maximum Wiener index applicable to the unbranched molecule can easily be calculated from the total number of "non-H" atoms (n) as follows:

It is always a sum of square numbers:

If n is even, the squares of the odd numbers between 0 and n are summed up.

If n is odd, the squares of the even numbers between 0 and n are summed.

examples for

n = 6: 1 ² + 3 ² + 5 ² = 35

n = 13: 2 ² + 4 ² + 6 ² + 8 ² + 10 ² + 12 ² = 364

One can use as a simplified calculation formula. ${\displaystyle n\cdot (n-1)\cdot (n+1)/6}$

Table of maximum values ​​for W

up to n = 21:

n	2	3	4th	5	6th	7th	8th	9	10	11	12	13	14th	15th	16	17th	18th	19th	20th	21st
(n-1) n = odd	1		3		5		7th		9		11		13		15th		17th		19th
(n-1) 2	1		9		25th		49		81		121		169		225		289		361
Sum = W	1		10		35		84		165		286		455		680		969		1330
(n-1) n = even		2		4th		6th		8th		10		12		14th		16		18th		20th
(n-1) 2		4th		16		36		64		100		144		196		256		324		400
Sum = W		4th		20th		56		120		220		364		560		816		1140		1540

literature

1. ↑ Harry Wiener (1947): Structural determination of paraffin boiling points . J. Am. Chem. Soc., 69, pp. 17-20. doi : 10.1021 / ja01193a005