B-tree

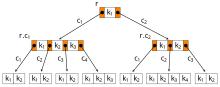
A B-tree ( English B-tree ) is in the computer science a data or index structure , often in databases and file systems is used. A B-tree is always a fully balanced tree that stores data sorted by key . It can be binary, but in general it is not a binary tree . The insertion, search and deletion of data in B-trees is possible in amortized logarithmic time. B-trees grow and shrink, unlike many search trees, from the leaves to the roots.

History and naming

The B-tree was developed in 1972 by Rudolf Bayer and Edward M. McCreight . It turned out to be the ideal data structure for managing indexes for the relational database model developed by Edgar F. Codd in 1970 . This combination led to the development of the first SQL - database system system R at IBM .

The inventors did not provide any explanation of the origin of the name B-tree . The most common interpretation is that B stands for balanced . Other interpretations are B for Bayer , Barbara (after his wife), Broad , Busch , Bushy , Boeing (since Rudolf Bayer worked for Boeing Scientific Research Labs ), banyan tree (a tree in which branches and roots create a network) or binary due to the binary search carried out within a node.

Idea and overview

In contrast to binary trees , a node in a B-tree can have more than 2 child nodes. This makes it possible to reduce the number of nodes to be read during a data search with a variable number of keys (or data values) per node. The maximum number of keys allowed depends on a parameter (sometimes also defined as , or in the literature ), the degree of branching (or order) of the B-tree. The meaning of differs depending on the definition: Either denotes the maximum number of child nodes - in this case the maximum number of keys permitted , or the minimum number of child nodes - in this case the maximum number of keys permitted . ${\displaystyle t}$ ${\displaystyle d}$ ${\displaystyle k}$ ${\displaystyle m}$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle (t-1)}$ ${\displaystyle 2t-1}$

B-trees are used, among other things, in database systems that have to deal with very large amounts of data, of which only a fraction fits into the main memory of a computer at the same time. The data is therefore stored persistently on background memory (e.g. hard drives ) and can be read in blocks . A node of the B-tree can then be read or saved as a block. Due to the large degree of branching in B-trees , the tree height and thus the number of (slow) read / write accesses is reduced. The variable set of keys per node also avoids frequent balancing of the tree.

A fully populated B-tree, in which the maximum allowed number of child nodes and h is defined as the height of the tree, is currently storing keys. For example, if you have chosen a correspondingly large size (e.g. ) at a height of , keys can already be saved. Since a search operation requires at most node accesses, a maximum of five tree nodes must be inspected for each search query in such a tree. ${\displaystyle t}$ ${\displaystyle t^{h}-1}$ ${\displaystyle t}$ ${\displaystyle t=1024}$ ${\displaystyle h=4}$ ${\displaystyle 1024^{4}-1=(2^{10})^{4}-1=2^{40}-1}$ ${\displaystyle h+1}$

Definitions

Figure 1: B-tree

1. A node of a B-tree stores
   • a variable number of keys (and optionally one data element assigned per key), ${\displaystyle s}$ ${\displaystyle k_{1},\ldots ,k_{s}}$
   • an isLeaf flag that indicates whether the node is a leaf or an inner node.
   • If it is an inner node, additional references to child nodes. ${\displaystyle s+1}$
2. For the keys in a B-tree, a sorting condition that is generalized compared to binary search trees applies:
   • All keys of a node are sorted in ascending order.
   • In the case of an inner node , its keys divide the key areas of its subtrees into sub-areas. Each key therefore represents a limit whose left-hand reference refers to smaller values ​​and whose right-hand reference refers to larger values. A subtree therefore only contains keys for which the following applies: ${\displaystyle x}$ ${\displaystyle x.k_{i}}$ ${\displaystyle x.c_{j}}$ ${\displaystyle s+1}$ ${\displaystyle x.k_{i}}$ ${\displaystyle x.c_{j}}$ ${\displaystyle k}$
     • ${\displaystyle k<x.k_{j}}$if ${\displaystyle j=1}$
     • ${\displaystyle x.k_{j-1}<k<x.k_{j}}$if ${\displaystyle j\in \{2,\ldots ,s\}}$
     • ${\displaystyle x.k_{j-1}<k}$if ${\displaystyle j=s+1}$
3. All leaf nodes of the B-tree are at the same depth. The depth of the leaf nodes is equal to the height of the tree. ${\displaystyle h}$
4. The following restriction applies to the number of child references or keys allowed per node. To do this, a constant is specified that indicates the minimum degree of branching of tree nodes. ${\displaystyle t}$
   • Have all nodes except the root
     • at least and at most keys and ${\displaystyle t-1}$ ${\displaystyle 2t-1}$
     • at least and at most child references if they are inner nodes. ${\displaystyle t}$ ${\displaystyle 2t}$
   • The root has
     • at least and at most keys if the B-tree is not empty, and ${\displaystyle 1}$ ${\displaystyle 2t-1}$
     • at least and at most child references if the height of the tree is greater than 0. ${\displaystyle 2}$ ${\displaystyle 2t}$

properties

The following applies to the height of a B-tree with stored data elements: ${\displaystyle h}$ ${\displaystyle n}$

${\displaystyle h\leq \log _{t}\left({n+1 \over 2}\right)+1}$

In the worst case, this means that tree nodes still have to be accessed to find a data element. However, the constant of this estimate is significantly lower than for (balanced) binary search trees with height : ${\displaystyle O(\log(n))}$ ${\displaystyle \log _{2}(n)}$

${\displaystyle {\log _{2}(n) \over {\log _{t}({n+1 \over 2})}}\approx \log _{2}(t)}$

With a minimum degree of branching of , a B-tree therefore requires access to ten times fewer nodes to find a data element. If access to a node dominates the duration of the entire operation (as is the case with access to background storage), the result is a ten-fold increase in execution speed. ${\displaystyle t=1024}$

Special cases and variants

For the special case , one speaks of 2-3-4 trees , since nodes in such a tree can have 2, 3 or 4 children. Common variants of the B-tree are B ⁺ -trees , in which the data is only stored in the leaves, and B * -trees , which are always too full due to a modified overflow treatment . Like the regular B-tree, all of these variants are often used in practice. ${\displaystyle t=2}$ ${\displaystyle 2/3}$

An R-tree can also be called a balanced tree as an extension of the B-tree.

Operations

Search

The search for a key provides the node that stores this key and the position within this node for which that applies . If the tree does not contain the key , the search returns the result does not contain . ${\displaystyle k}$ ${\displaystyle x}$ ${\displaystyle j}$ ${\displaystyle k=x.k_{j}}$ ${\displaystyle k}$

The search is carried out in the following steps:

1. The search begins with the root node as the current node . ${\displaystyle r}$ ${\displaystyle x}$
2. Is an inner knot ${\displaystyle x}$
   • the position of the smallest key that is greater than or equal is determined. ${\displaystyle j}$ ${\displaystyle k}$
   • If there is such a position , ${\displaystyle j}$
     • but is , the key you are looking for can only be contained in the root subtree . The search therefore continues with step 2 and the node as the current node. ${\displaystyle k\neq x.k_{j}}$ ${\displaystyle x.c_{j}}$ ${\displaystyle x.c_{j}}$
     • otherwise the key was found and is returned as the result. ${\displaystyle (x,j)}$
   • If no such position exists, the key is larger than all keys stored in the current node. In this case, the key you are looking for can only be contained in the subtree to which the last child reference points. In this case the search continues with step 2 and the node as the current node. ${\displaystyle x.c_{x.s+1}}$ ${\displaystyle x.c_{x.s+1}}$
3. Is a leaf knot ${\displaystyle x}$
   • Will be searched in the keys of . ${\displaystyle k}$ ${\displaystyle x}$
   • If the key is found in position , the result is not included , otherwise it is not included . ${\displaystyle j}$ ${\displaystyle (x,j)}$

Figure 2: Search in the B-tree

Figure 2 shows the situation during the search for the key . In step 2 from the above algorithm, the smallest position for which applies is sought in the current node . In the concrete example, the position is found where applies. The search is therefore continued in the sub -tree marked in red because, due to the B-tree property (2), the key sought can only be located in this sub -tree . ${\displaystyle k=9}$ ${\displaystyle x}$ ${\displaystyle j}$ ${\displaystyle 9\leq x.k_{j}}$ ${\displaystyle 2}$ ${\displaystyle 5\leq 9\leq 13}$ ${\displaystyle x.c_{2}}$ ${\displaystyle 9}$

Insert

Figure 3: Splitting a full B-tree node.

A key is always inserted in a B-tree in a leaf node. ${\displaystyle k}$

1. In a preparatory step, the leaf node is searched for into which it must be inserted. Precautions are taken so that the insert operation does not violate the B-tree conditions and create a node that contains more than keys. ${\displaystyle x_{\mathrm {insert} }}$ ${\displaystyle 2t-1}$
2. In a final step, it is inserted locally into , taking the sort order into account . ${\displaystyle k}$ ${\displaystyle x}$

The search for is as described under Search with two differences . These differences are: ${\displaystyle x_{\mathrm {insert} }}$

• A new key is always inserted in a leaf node. Insertion must therefore always be preceded by a complete search which shows that the key does not yet exist and which determines in which node it is to be entered. This can only be a leaf node, because this statement is only permissible after searching through the entire height of the tree. However, the search is canceled in an inner node if the key has already been found there and an insertion is therefore not necessary. ${\displaystyle k}$ ${\displaystyle k}$ ${\displaystyle k}$
• Before the search descends to a child node , it is checked whether it is full, i. H. already contains keys. In this case, it is shared as a precaution. This guarantees that the insert operation can be performed with a single tree descent and that no subsequent repair measures need to be performed to restore the B-tree conditions. ${\displaystyle x.c_{j}}$ ${\displaystyle x.c_{j}}$ ${\displaystyle 2t-1}$ ${\displaystyle x.c_{j}}$

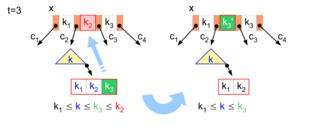
Splitting a full tree node happens as shown in Figure 3. The search has arrived at the node and would descend to the child node (red arrow). That is, the search position is . Since this child node is full, it must be split prior to descent to guarantee that insertion is possible. A full node always has an odd number of keys. The middle one (in the figure is the key ) is inserted in the current node at the search position . The node is divided into two nodes of the same size, each with keys, and these are linked via the two new pointer positions (two red arrows in the result). The search then either descends into the subtree or descends, depending on whether or not the key to be inserted is less than or equal to the middle key of the split node. ${\displaystyle x}$ ${\displaystyle x.c_{2}}$ ${\displaystyle j=2}$ ${\displaystyle 2t-1}$ ${\displaystyle x.c_{2}.k_{3}}$ ${\displaystyle j}$ ${\displaystyle x.c_{2}}$ ${\displaystyle t-1}$ ${\displaystyle x.c_{2}}$ ${\displaystyle x.c_{3}}$

Clear

Deleting a key is a more complex operation than inserting it, as the case that a key is deleted from an inner node must also be considered here. The process is like looking for a suitable place to insert a key, with the difference that, before descending into a subtree, a check is made to determine whether it contains enough keys ( ) to carry out a possible delete operation without violating the B-tree Conditions to be able to carry out. This procedure is analogous to inserting and avoids subsequent repair measures. ${\displaystyle k_{\mathrm {delete} }}$ ${\displaystyle \geq t}$

If the subtree selected by the search for descent contains the minimum number of keys ( ), either a move or a merge is performed. If the key you are looking for is found in a leaf node, it can be deleted there directly. If, on the other hand, it is found in an inner node, the deletion takes place as described in Deleting from inner nodes . ${\displaystyle t-1}$

shift

Figure 4: Moving a key in the B-tree.

If the subtree selected for descent contains only the minimum number of keys , but a preceding or following sibling node has at least keys, a key is moved to the selected node, as shown in Figure 4. The search selected here for the descent (da ), but this node only contains keys (red arrow). Since the following sibling node contains a sufficient number of keys, the smallest key can be moved from there to the parent node in order to move the key as an additional key to the node selected for relegation. To do this, the left subtree of becomes the new right subtree of the moved key . One can easily convince oneself that this rotation preserves the sorting conditions, since the requirement applies to all keys in the moved subtree before and after the move . A symmetric operation can be performed to move a key from a previous sibling. ${\displaystyle t-1}$ ${\displaystyle t}$ ${\displaystyle x.c_{2}}$ ${\displaystyle x.k_{1}<k_{\mathrm {delete} }<x.k_{2}}$ ${\displaystyle t-1}$ ${\displaystyle x.c_{3}}$ ${\displaystyle x.c_{3}.k_{1}}$ ${\displaystyle x.k_{2}}$ ${\displaystyle x.c_{3}.k_{1}}$ ${\displaystyle x.k_{2}}$ ${\displaystyle k}$ ${\displaystyle x.k_{2}\leq k\leq x.c_{3}.k_{1}}$

merger

Figure 5: Merging two B-tree child nodes.

If both the subtree selected for the descent and its immediately preceding and following sibling nodes contain exactly the minimum number of keys, a move is not possible. In this case, the selected subtree is merged with the preceding or following sibling nodes as shown in Figure 5. For this purpose, the key from the parent node , which separates the value ranges of the keys in the two nodes to be merged, is moved into the merged node as the middle key. The two references to the now merged child nodes are replaced by a reference to the new node. ${\displaystyle x.c_{2}}$ ${\displaystyle x}$

Since the algorithm ensures that a node contains at least the keys required by the B-tree conditions instead of the ones required by the B-tree conditions, the algorithm ensures that the parent node contains a sufficient number of keys to provide a key for the merger. Only in the case that two children of the root node are merged, this condition can be violated, since the search begins at this node. The B-tree conditions require at least one key for the root node if the tree is not empty. When the last two children of the root node are merged, however, its last key is moved to the newly created single child, which leads to an empty root node in a non-empty tree. In this case, the empty root node is deleted and replaced by its only child. ${\displaystyle t}$ ${\displaystyle t-1}$ ${\displaystyle x}$

Delete from inner nodes

Figure 6: Deleting a key from an inner node.

If the key to be deleted is already found in an inner node ( in Figure 6), it cannot be deleted directly because it is required to separate the value ranges of its two subtrees and . In this case, its symmetrical predecessor (or its symmetrical successor) is deleted and copied in its place. The symmetrical predecessor is the largest leaf node in the left subtree , so it is located on the far right. The symmetrical successor is accordingly the smallest leaf node in the right subtree and is located there on the far left. The decision as to which subtree to descend for the deletion is made dependent on which one contains sufficient keys. If both only have the minimum number of keys, the subtrees are merged. This means that there is no longer any need to separate the value ranges and the key can be deleted directly. ${\displaystyle k_{\mathrm {delete} }}$ ${\displaystyle k_{\mathrm {delete} }=x.k_{2}}$ ${\displaystyle x.c_{2}}$ ${\displaystyle x.c_{3}}$ ${\displaystyle x.c_{2}}$ ${\displaystyle x.c_{3}}$

example

Figure 7: Evolution of a B-tree

Figure 7 shows the development of a B-tree with a minimal degree of branching . Nodes in such a tree can store a minimum of one and a maximum of three keys and have between two and four references to child nodes. One therefore speaks of a 2-3-4 tree . In a practical application, however, one would use a B-tree with a significantly greater degree of branching. ${\displaystyle t=2}$

The following operations were performed on a 2-4 tree (see Figure 7):

• a – c) Insertion of 5, 13 and 27 into an initially empty tree.
• d – e) Inserting 9 results in splitting the root node.
• f) inserting 7 in a leaf node.
• g – h) Inserting 3 results in splitting a node.
• i – j) In order to be able to delete 9, a key is moved from a sibling node.
• k – l) Deleting 7 leads to the merging of two nodes.
• m) Erasing 5 from a sheet.
• n – q) Deleting 3 leads to the merging of the last two children of the root node. The resulting empty root node is replaced by its only child.

See also

• R-tree is a related indexing method for multidimensional data.
• B ⁺ -tree and B * -tree are B-tree variants.
• 2-3-4-tree is a special case of a B-tree with a minimal degree of branching . ${\displaystyle t=2}$
• AVL tree
• Red-black tree

literature

German

• Niklaus Wirth : Algorithms and data structures with Modula-2. Stuttgart 1986, ISBN 3-519-02260-5 .
• T. Ottmann, P. Widmayer: Algorithms and Data Structures-3. Spektrum, Heidelberg / Berlin / Oxford 1996, ISBN 3-8274-0110-0 , pp. 317-327.
• Alfons Kemper , André Eickler: Database systems. Oldenbourg Verlag, Munich 2009, ISBN 978-3-486-59018-0 , p. 218

English

• R. Bayer , E. McCreight: Organization and Maintenance of Large Ordered Indexes. In: Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control. 1970, pp. 107-141.
• R. Bayer , E. McCreight: Organization and Maintenance of Large Ordered Indexes. In: Acta Informatica. Volume 1, 1972, pp. 173-189.
• R. Bayer, E. McCreight: Symmetric binary B-Trees: data structure and maintenance algorithms. In: Acta Informatica. Volume 1, 1972, pp. 290-306.

Web links

Tools for trying out B-trees:

• cs.usfca.edu - Animated JavaScript version by David Galles
• slady.net - B-tree Java applet
• ats.oka.nu - Flash applet

Individual evidence

1. ^ Thomas H. Cormen, Charles E. Leiserson , Ronald L. Rivest , Clifford Stein: Introduction to Algorithms . 2nd Edition. MIT Press, Cambridge (Massachusetts) 2001, ISBN 0-262-03293-7 , pp. 439 .
2. ^ R. Bayer, E. McCreight: Organization and Maintenance of Large Ordered Indices . In: Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control (=  SIGFIDET '70 ). ACM, New York, NY, USA 1970, p. 107–141 , doi : 10.1145 / 1734663.1734671 ( acm.org [accessed February 20, 2019]).

This version was added to the list of articles worth reading on December 7, 2005 .