Golden rule of accumulation

The golden rule of accumulation of Edmund Phelps has it that in the Solow model of consumption per capita or per worker is then maximized when the interest rate equal to the growth rate of the gross domestic product is. The derivation of this rule is based on a number of simplifying assumptions. The rule has also been further developed, for example by taking consumer time preferences into account ( Ramsey rule ).

The interest rate obtained with the aid of the golden rule could then be used as the “equilibrium real interest rate” in the Taylor rule to determine the Taylor interest rate .

Assumptions

Some assumptions are made to derive the rule:

1. The growth rate of population / employment L is given exogenously . The supply of labor L is growing as the population with a "natural growth rate" n : where the derivation of a variable with respect to time is
   ${\displaystyle {\frac {{\dot {L}}(t)}{L(t)}}={\hat {L}}(t)=:n}$ ${\displaystyle {\dot {L}}(t)}$ ${\displaystyle {\dot {L}}(t)={\frac {dL(t)}{dt}}}$
2. The product Y is divided into consumption C and investment I . For the sake of simplicity, exports and imports are therefore not taken into account ( closed economy ).
3. The savings S is used to finance investments I in the same amount. (" S equals I ") or
   ${\displaystyle Y(t)=C(t)+I(t)}$ ${\displaystyle Y(t)=C(t)+S(t)}$
4. A steady-state growth is assumed, i.e. all economic variables grow at the same rate of growth, which - if there is no technical progress - must correspond to the natural growth rate n of the labor supply.
5. Finally a production function is assumed, that is, the production or the output Y (the quantity thereof) depends on how much of the two production factors labor force L and “capital” (the means of production ) K are used. In addition, the simplifying assumption is made about the form of the production function that it is linearly homogeneous. Linearly homogeneous production functions have the mathematical property that they can be transformed in such a way that production per worker Y / L , denoted as y , is a function of the capital input per worker K / L , denoted as k .

Under all these assumptions, a mathematical relationship (function) can be formulated according to which the consumption per worker C / L is determined by the capital input per worker K / L ( denoted as k ).

This C / L is to be maximized by deriving for k using the usual mathematical method and setting the result to zero (the first derivative is set to zero in order to find the extreme point ).

In detail:

Steady state growth rate

The increase in the capital stock is equal to the investments I , which in turn are financed by the savings S : ${\displaystyle {\dot {K}}}$

${\displaystyle {\dot {K}}(t)=I(t)=S(t)}$

Savings rate: ${\displaystyle s={\frac {S(t)}{Y(t)}}={\frac {{\dot {K}}(t)}{Y(t)}}}$

The consumption function: with ${\displaystyle C(t)=(1-s)Y(t)}$ ${\displaystyle s\in [0;1]}$

Capital intensity: ${\displaystyle k(t)={\frac {K(t)}{L(t)}}}$

Per capita production: ${\displaystyle y(t)={\frac {Y(t)}{L(t)}}}$

Production function :

${\displaystyle Y(t)=F(K(t),L(t))}$

Linear homogeneous production function

${\displaystyle F(\lambda K(t),\lambda L(t))=\lambda F(K(t),L(t))}$

${\displaystyle \lambda ={\frac {1}{L}}:}$

${\displaystyle {\frac {1}{L}}\cdot Y(t)=F\left({\frac {1}{L}}\cdot K(t),{\frac {1}{L}}\cdot L(t)\right)}$

so the production function can also be expressed in per capita terms. The production per worker depends on the capital endowment per worker (capital intensity):

${\displaystyle y(t)=F(k(t),1)=f[k(t)]}$

The growth rate of population / employment L is given exogenously :

${\displaystyle {\frac {{\dot {L}}(t)}{L(t)}}={\hat {L}}(t)=n}$

Steady state growth rate, all sizes should grow at the same rate:

${\displaystyle {\frac {{\dot {Y}}(t)}{Y(t)}}={\frac {{\dot {L}}(t)}{L(t)}}={\frac {{\dot {K}}(t)}{K(t)}}=n}$

${\displaystyle {\frac {{\dot {K}}(t)}{K(t)}}={\hat {K}}(t)=s\cdot {\frac {Y(t)}{K(t)}}=s{\frac {y(t)}{k(t)}}=n}$

${\displaystyle s{\frac {y(t)}{k(t)}}=s{\frac {f(k(t))}{k(t)}}=n}$

${\displaystyle sf(k(t))=nk(t)}$

Maximizing per capita consumption

This graph shows how the capital stock and the associated savings rate maximize the economy's long-term equilibrium consumption . The maximum is . ${\displaystyle k^{\mathrm {gold} }}$ ${\displaystyle s^{\mathrm {gold} }}$ ${\displaystyle c^{*}}$ ${\displaystyle c^{\mathrm {gold} }}$

At what steady-state growth rate is consumption per capita

${\displaystyle {\frac {C(t)}{L(t)}}}$

maximized?

${\displaystyle {\frac {C(t)}{L(t)}}=(1-s){\frac {Y(t)}{L(t)}}=(1-s)y(t)=(1-s)f(k(t))}$

According to the steady state:

${\displaystyle s\cdot f(k(t))=(n+\delta )\cdot k}$

So:

${\displaystyle {\frac {C(t)}{L(t)}}=f(k(t))-(n+\delta )\cdot k}$

Maximizing per capita consumption with regard to k means deriving from k and setting it to zero:

${\displaystyle f^{\prime }(k(t))-(n+\delta )=0}$

Golden rule of accumulation

The marginal productivity of capital must therefore be equal to the growth rate . Neoclassically it is assumed that the marginal productivity of capital is equal to the price of the capital employed, i.e. equal to the rate of profit or the interest rate. ${\displaystyle f^{\prime }(k)}$ ${\displaystyle (n+\delta )}$

Additional calculation for the marginal productivity of capital

Marginal productivity of capital as a partial derivative of F ( K , L ) with respect to K :

${\displaystyle {\frac {\partial F(K,L)}{\partial K}}}$

Linear homogeneity:

${\displaystyle F(K,L)=L\cdot F\left({\frac {K}{L}},1\right)=L\cdot f(k)}$

Partial calculation (using the chain rule ):

${\displaystyle {\frac {\partial F({\frac {K}{L}},1)}{\partial K}}={\frac {\partial F({\frac {K}{L}},1)}{\partial {\frac {K}{L}}}}\cdot {\frac {\partial {\frac {K}{L}}}{\partial K}}}$

${\displaystyle =f^{\prime }(k){\frac {1}{L}}}$

So overall:

${\displaystyle {\frac {\partial F(K,L)}{\partial K}}=f^{\prime }(k)}$

Empirical review

Profit rate equals investment rate

The golden rule of accumulation says that in the optimal case the interest rate should be equal to the steady-state growth rate, in particular:

${\displaystyle i={\frac {{\dot {K}}(t)}{K(t)}}}$

Multiply left and right by K and divide by Y , then you get:

${\displaystyle {\frac {i\cdot K(t)}{Y(t)}}={\frac {{\dot {K}}(t)}{Y(t)}}}$,

in which

${\displaystyle {\dot {K}}(t)=I(t)}$

is.

Investments in proportion to profits

On the left of the equation is the profit ratio ( profit ratio , the share of profits in GDP) and on the right is the investment ratio , the share of investments in GDP. Whether both are actually the same can be checked empirically .

If the investment rate (equal to the savings rate , including depreciation ) is higher than the profit rate (including depreciation, i.e. equal to the cash flow rate), then (according to Lutz Arnold, p. 54) there is “dynamic inefficiency”. According to Arnold, studies for the OECD countries come to the conclusion that it was more likely the other way round, the profit rate tending to be higher than the investment rate.

The profit rate was around a third, the investment rate around 10% to 20%. The profit quota is inclusive of taxes. A study by the IMF comes to the conclusion that the global savings and investment rate, measured in terms of gross domestic product , decreased from around 24% in 1970 to around 22% in 2004.

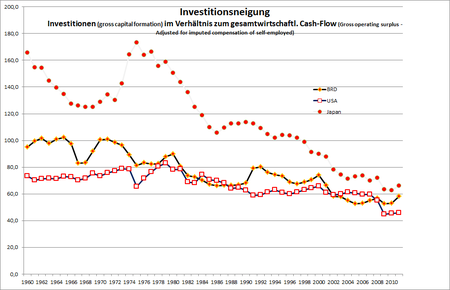
While this result refutes "dynamic inefficiency" according to Arnold, on the other hand the question arises whether the rule "Today's profits are tomorrow's investments (and the jobs of the day after tomorrow)", the so-called GIB formula , is correct if the The investment quota is actually noticeably lower than the profit quota, or as other studies show, lags behind the profit quota ( investment emergency ). The figure shows the gross fixed capital formation in relation to the macroeconomic " cash flow ", here profits before deduction of taxes plus depreciation. The propensity to invest, as defined in this way , tends to decline in the countries of the triad USA, Japan and Germany.

Interest rate equals growth rate

The golden rule can also be checked directly by comparing the rate of GDP growth to the interest rate. The figure shows the difference between the GDP growth rate and the long-term interest rate . According to this, long-term interest rates have tended to be too low until the 1970s and too high since the 1980s. Since the 1980s, the incomes of the production factor capital have been rather too high, measured by the golden rule.

Long-term interest rate minus GDP growth rate

literature

• Lutz Arnold: Growth Theory . Vahlen Verlag, Munich 1997, ISBN 3-8006-2242-4

Web links

• Wirtschaftsdienst 1999/11, Jörg Hinze, Kai Kirchesch: "Relation between profits and investments loosened" (PDF file)
• Analysis of the IMF on global savings and investment behavior (in English) (PDF file; 285 kB)