List of small groups

The following list contains a selection of finite groups of small order .

This list can be used to find out which known finite groups a group G is isomorphic to . First you determine the order of G and compare it with the groups of the same order listed below. If it is known whether G abelian ( commutative ), some groups can be excluded. Then one compares the order of individual elements of G with the elements of the listed groups, whereby one can clearly determine G except for isomorphism.

glossary

The following terms are used in the following list:

• ${\displaystyle \mathbb {Z} _{n}}$is the cyclic group of order (also written as or ). ${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle \mathbb {Z} /n\mathbb {Z} }$
• ${\displaystyle D_{n}}$is the dihedral group of the order . ${\displaystyle 2n}$
• ${\displaystyle S_{n}}$is the symmetric group of degree , with n ! Permutations of elements. ${\displaystyle n}$ ${\displaystyle n}$
• ${\displaystyle A_{n}}$is the alternating group of degree , with permutations of elements for . ${\displaystyle n}$ ${\displaystyle n!/2}$ ${\displaystyle n}$ ${\displaystyle n\geq 2}$
• ${\displaystyle \mathrm {Dic} _{n}}$is the dicyclic group of the order . ${\displaystyle 4n}$
• ${\displaystyle V_{4}}$is the Klein group of four of the order . ${\displaystyle 4}$
• ${\displaystyle Q_{4n}}$is the quaternion group of order for . ${\displaystyle 4n}$ ${\displaystyle n\geq 2}$

The notation is used to denote the direct product of the groups and . It is noted whether a group is abelian or simple . (For groups of the order , the simple groups are exactly the cyclic groups , including from the set of prime numbers .) In the cycle graphs of the groups, the neutral element is represented by a filled black circle. Order is the smallest order for which the group structure is not uniquely determined by the cycle graph: The nonabelian modular group and have the same cycle graph and the same (modular) subgroup lattice , but are not isomorphic. ${\displaystyle G\times H}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle n<60}$ ${\displaystyle \mathbb {Z} _{n}}$ ${\displaystyle n}$ ${\displaystyle 16}$ ${\displaystyle \mathbb {Z} _{8}\times \mathbb {Z} _{2}}$

It should be noted that means that there are 3 subgroups of the type (not the minor class of ). ${\displaystyle 3\cdot \mathbb {Z} _{2}}$ ${\displaystyle \mathbb {Z} _{2}}$ ${\displaystyle \mathbb {Z} _{2}}$

For each order, the cyclic group is specified first, followed by other Abelian groups and then possibly non-Abelian groups:

List of all groups up to order 20

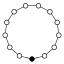
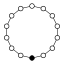
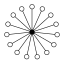
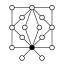
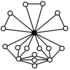
order	group	Real subgroups	properties	Cycle graph
1	${\displaystyle \mathbb {Z} _{1}\cong S_{1}\cong A_{2}}$   ( trivial group )	-	abelian, cyclical
2	${\displaystyle \mathbb {Z} _{2}\cong S_{2}\cong D_{1}}$   ( Group Z 2 )	-	abelian, simple , cyclical, smallest nontrivial group
3	${\displaystyle \mathbb {Z} _{3}\cong A_{3}}$	-	abelian, simple, cyclical
4th	${\displaystyle \mathbb {Z} _{4}\cong \mathrm {Dic} _{1}}$	${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle V_{4}\cong \mathbb {Z} _{2}^{2}\cong D_{2}}$   ( Klein's group of four )	${\displaystyle 3\cdot \mathbb {Z} _{2}}$	abelian, the smallest non-cyclic group
5	${\displaystyle \mathbb {Z} _{5}}$	-	abelian, simple, cyclical
6th	${\displaystyle \mathbb {Z} _{6}\cong \mathbb {Z} _{2}\times \mathbb {Z} _{3}}$	${\displaystyle \mathbb {Z} _{3}}$, ${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle S_{3}\cong D_{3}}$   ( Symmetrical group )	${\displaystyle \mathbb {Z} _{3}}$, ${\displaystyle 3\cdot \mathbb {Z} _{2}}$	smallest non-Abelian group
7th	${\displaystyle \mathbb {Z} _{7}}$	-	abelian, simple, cyclical
8th	${\displaystyle \mathbb {Z} _{8}}$	${\displaystyle \mathbb {Z} _{4}}$, ${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{4}}$	${\displaystyle 2\cdot \mathbb {Z} _{4}}$, , ${\displaystyle 3\cdot \mathbb {Z} _{2}}$ ${\displaystyle D_{2}}$	abelian
	${\displaystyle \mathbb {Z} _{2}^{3}\cong D_{2}\times \mathbb {Z} _{2}}$	${\displaystyle 7\cdot \mathbb {Z} _{2}}$, ${\displaystyle 7\cdot D_{2}}$	abelian
	${\displaystyle D_{4}}$	${\displaystyle \mathbb {Z} _{4}}$, , ${\displaystyle 2\cdot D_{2}}$ ${\displaystyle 5\cdot \mathbb {Z} _{2}}$	notabelsch
	${\displaystyle Q_{8}\cong \mathrm {Dic} _{2}}$   ( Quaternion group )	${\displaystyle 3\cdot \mathbb {Z} _{4}}$, ${\displaystyle \mathbb {Z} _{2}}$	nichtabelsch; the smallest Hamiltonian group
9	${\displaystyle \mathbb {Z} _{9}}$	${\displaystyle \mathbb {Z} _{3}}$	abelian, cyclical
	${\displaystyle \mathbb {Z} _{3}^{2}}$	${\displaystyle 4\cdot \mathbb {Z} _{3}}$	abelian
10	${\displaystyle \mathbb {Z} _{10}\cong \mathbb {Z} _{2}\times \mathbb {Z} _{5}}$	${\displaystyle \mathbb {Z} _{5}}$, ${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle D_{5}}$	${\displaystyle \mathbb {Z} _{5}}$, ${\displaystyle 5\cdot \mathbb {Z} _{2}}$	notabelsch
11	${\displaystyle \mathbb {Z} _{11}}$	-	abelian, simple, cyclical
12	${\displaystyle \mathbb {Z} _{12}\cong \mathbb {Z} _{4}\times \mathbb {Z} _{3}}$	${\displaystyle \mathbb {Z} _{6}}$, , , ${\displaystyle \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{3}}$ ${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{6}\cong \mathbb {Z} _{2}^{2}\times \mathbb {Z} _{3}\cong D_{2}\times \mathbb {Z} _{3}}$	${\displaystyle 3\cdot \mathbb {Z} _{6}}$, , , ${\displaystyle \mathbb {Z} _{3}}$ ${\displaystyle D_{2}}$ ${\displaystyle 3\cdot \mathbb {Z} _{2}}$	abelian
	${\displaystyle D_{6}\cong D_{3}\times \mathbb {Z} _{2}}$	${\displaystyle \mathbb {Z} _{6}}$, , , , ${\displaystyle 2\cdot D_{3}}$ ${\displaystyle 3\cdot D_{2}}$ ${\displaystyle \mathbb {Z} _{3}}$ ${\displaystyle 7\cdot \mathbb {Z} _{2}}$	notabelsch
	${\displaystyle A_{4}}$  ( Group A 4 )	${\displaystyle D_{2}}$, , ${\displaystyle 4\cdot \mathbb {Z} _{3}}$ ${\displaystyle 3\cdot \mathbb {Z} _{2}}$	nichtabelsch; smallest group showing that the inverse of Lagrange's theorem is incorrect: no subgroup of order 6
	${\displaystyle \mathrm {Dic} _{3}}$( here link table )	${\displaystyle \mathbb {Z} _{6}}$, , , ${\displaystyle 3\cdot \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{3}}$ ${\displaystyle \mathbb {Z} _{2}}$	notabelsch
13	${\displaystyle \mathbb {Z} _{13}}$	-	abelian, simple, cyclical
14th	${\displaystyle \mathbb {Z} _{14}\cong \mathbb {Z} _{2}\times \mathbb {Z} _{7}}$	${\displaystyle \mathbb {Z} _{7}}$, ${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle D_{7}}$	${\displaystyle \mathbb {Z} _{7}}$, ${\displaystyle 7\cdot \mathbb {Z} _{2}}$	notabelsch
15th	${\displaystyle \mathbb {Z} _{15}\cong \mathbb {Z} _{3}\times \mathbb {Z} _{5}}$	${\displaystyle \mathbb {Z} _{5}}$, ${\displaystyle \mathbb {Z} _{3}}$	Abelian, cyclic (see "Every group of order 15 is cyclic." )
16	${\displaystyle \mathbb {Z} _{16}}$	${\displaystyle \mathbb {Z} _{8}}$, , ${\displaystyle \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle \mathbb {Z} _{2}^{4}}$	${\displaystyle 15\cdot \mathbb {Z} _{2}}$, , ${\displaystyle 35\cdot D_{2}}$ ${\displaystyle 15\cdot \mathbb {Z} _{2}^{3}}$	abelian
	${\displaystyle \mathbb {Z} _{4}\times \mathbb {Z} _{2}^{2}}$	${\displaystyle 7\cdot \mathbb {Z} _{2}}$, , , , ${\displaystyle 4\cdot \mathbb {Z} _{4}}$ ${\displaystyle 7\cdot D_{2}}$ ${\displaystyle \mathbb {Z} _{2}^{3}}$ ${\displaystyle 6\cdot \mathbb {Z} _{4}\times \mathbb {Z} _{2}}$	abelian
	${\displaystyle \mathbb {Z} _{8}\times \mathbb {Z} _{2}}$	${\displaystyle 3\cdot \mathbb {Z} _{2}}$, , , , ${\displaystyle 2\cdot \mathbb {Z} _{4}}$ ${\displaystyle D_{2}}$ ${\displaystyle 2\cdot \mathbb {Z} _{8}}$ ${\displaystyle \mathbb {Z} _{4}\times \mathbb {Z} _{2}}$	abelian
	${\displaystyle \mathbb {Z} _{4}^{2}}$	${\displaystyle 3\cdot \mathbb {Z} _{2}}$, , , ${\displaystyle 6\cdot \mathbb {Z} _{4}}$ ${\displaystyle D_{2}}$ ${\displaystyle 3\cdot \mathbb {Z} _{4}\times \mathbb {Z} _{2}}$	abelian
	${\displaystyle D_{8}}$	${\displaystyle \mathbb {Z} _{8}}$, , , , ${\displaystyle 2\cdot D_{4}}$ ${\displaystyle 4\cdot D_{2}}$ ${\displaystyle \mathbb {Z} _{4}}$ ${\displaystyle 9\cdot \mathbb {Z} _{2}}$	notabelsch
	${\displaystyle D_{4}\times \mathbb {Z} _{2}}$	${\displaystyle 4\cdot D_{4}}$, , , , , ${\displaystyle \mathbb {Z} _{4}\times \mathbb {Z} _{2}}$ ${\displaystyle 2\cdot \mathbb {Z} _{2}^{3}}$ ${\displaystyle 13\cdot \mathbb {Z} _{2}^{2}}$ ${\displaystyle 2\cdot \mathbb {Z} _{4}}$ ${\displaystyle 11\cdot \mathbb {Z} _{2}}$	notabelsch
	${\displaystyle Q_{16}\cong \mathrm {Dic_{4}} }$	${\displaystyle \mathbb {Z} _{8}}$, , , ${\displaystyle 2\cdot Q_{8}}$ ${\displaystyle 5\cdot \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{2}}$	notabelsch
	${\displaystyle Q_{8}\times \mathbb {Z} _{2}}$	${\displaystyle 3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}}$, , , , ${\displaystyle 4\cdot Q_{8}}$ ${\displaystyle 6\cdot \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 3\cdot \mathbb {Z} _{2}}$	non-Abelian, Hamiltonian group
	Quasi-dihedral group	${\displaystyle \mathbb {Z} _{8}}$, , , , , ${\displaystyle Q_{8}}$ ${\displaystyle D_{4}}$ ${\displaystyle 3\cdot \mathbb {Z} _{4}}$ ${\displaystyle 2\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 5\cdot \mathbb {Z} _{2}}$	notabelsch
	Nonabelian non-Hamiltonian modular group	${\displaystyle 2\cdot \mathbb {Z} _{8}}$, , , , ${\displaystyle \mathbb {Z} _{4}\times \mathbb {Z} _{2}}$ ${\displaystyle 2\cdot \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 3\cdot \mathbb {Z} _{2}}$	notabelsch
	Semi-direct product (see here ) ${\displaystyle \mathbb {Z} _{4}\rtimes \mathbb {Z} _{4}}$	${\displaystyle 3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}}$, , , ${\displaystyle 6\cdot \mathbb {Z} _{4}}$ ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 3\cdot \mathbb {Z} _{2}}$	notabelsch
	The group generated by Pauli matrices .	${\displaystyle 3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}}$, , , , , ${\displaystyle 3\cdot D_{4}}$ ${\displaystyle Q_{8}}$ ${\displaystyle 4\cdot \mathbb {Z} _{4}}$ ${\displaystyle 3\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 7\cdot \mathbb {Z} _{2}}$	notabelsch
	${\displaystyle G_{4,4}=V_{4}\rtimes \mathbb {Z} _{4}}$	${\displaystyle 2\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{4}}$, , , , ${\displaystyle \mathbb {Z} _{2}\times \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 4\cdot \mathbb {Z} _{4}}$ ${\displaystyle 7\cdot \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$ ${\displaystyle 7\cdot \mathbb {Z} _{2}}$	notabelsch
17th	${\displaystyle \mathbb {Z} _{17}}$	-	abelian, simple, cyclical
18th	${\displaystyle \mathbb {Z} _{18}\cong \mathbb {Z} _{9}\times \mathbb {Z} _{2}}$	${\displaystyle \mathbb {Z} _{9},\mathbb {Z} _{6},\mathbb {Z} _{3},\mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle \mathbb {Z} _{6}\times \mathbb {Z} _{3}}$	${\displaystyle \mathbb {Z} _{6},\mathbb {Z} _{3},\mathbb {Z} _{2}}$	abelian
	${\displaystyle D_{9}}$		notabelsch
	${\displaystyle S_{3}\times \mathbb {Z} _{3}}$		notabelsch
	${\displaystyle (\mathbb {Z} _{3}\times \mathbb {Z} _{3})\rtimes _{\alpha }\mathbb {Z} _{2}}$ With ${\displaystyle \alpha (1)={\begin{pmatrix}2&0\\0&2\end{pmatrix}}}$		notabelsch
19th	${\displaystyle \mathbb {Z} _{19}}$	-	abelian, simple, cyclical
20th	${\displaystyle \mathbb {Z} _{20}\cong \mathbb {Z} _{5}\times \mathbb {Z} _{4}}$	${\displaystyle \mathbb {Z} _{10},\mathbb {Z} _{5},\mathbb {Z} _{4},\mathbb {Z} _{2}}$	abelian, cyclical
	${\displaystyle \mathbb {Z} _{10}\times \mathbb {Z} _{2}\cong \mathbb {Z} _{5}\times \mathbb {Z} _{2}\times \mathbb {Z} _{2}}$	${\displaystyle \mathbb {Z} _{5},\mathbb {Z} _{2}}$	abelian
	${\displaystyle Q_{20}\cong \mathrm {Dic} _{5}}$		notabelsch
	${\displaystyle \mathbb {Z} _{5}\rtimes \mathbb {Z} _{4}\cong }$ AGL 1 (5)		notabelsch
	${\displaystyle D_{10}\cong D_{5}\times \mathbb {Z} _{2}}$	${\displaystyle \mathbb {Z} _{10},D_{5},\mathbb {Z} _{5},5\cdot V_{4},6\cdot \mathbb {Z} _{2}}$	notabelsch

Simple structure sentences

The following statements are very elementary structural sentences, the effects of which are clearly reflected in the list above.

• If a prime number, then every group of the order is isomorphic to the cyclic group . ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle \mathbb {Z} _{p}}$

• If a prime number, then every group of the order is Abelian, more precisely isomorphic to the cyclic group or to the direct product . ${\displaystyle p}$ ${\displaystyle p^{2}}$ ${\displaystyle \mathbb {Z} _{p^{2}}}$ ${\displaystyle \mathbb {Z} _{p}\times \mathbb {Z} _{p}}$

• If a prime number, then every group of the order is isomorphic to the cyclic group or to the dihedral group . ${\displaystyle p}$ ${\displaystyle 2p}$ ${\displaystyle \mathbb {Z} _{2p}}$ ${\displaystyle D_{p}}$

• If and are prime numbers with and is not a divisor of , then every group of the order is isomorphic to the cyclic group . ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle q<p}$ ${\displaystyle q}$ ${\displaystyle p-1}$ ${\displaystyle pq}$ ${\displaystyle \mathbb {Z} _{pq}}$

"The SmallGroups Library"

The computer algebra system GAP contains the program library SmallGroups Library, which contains a description of groups of small orders. These are all listed except for isomorphism. At the moment (GAP version 4.8.8) the library contains groups of the following order:

• all of the order up to 2000, except for the 49,487,365,422 groups of the order 1024 (remaining 423,164,062 groups);
• all groups whose order n is not divided by p ³ for any prime p , for n ≤ 50,000 (395,703 groups);
• all of order p ⁷ , where p is one of the prime numbers 3, 5, 7 and 11 (907,489 groups);
• all of order p ⁿ with an arbitrary prime number p and n ≤ 6;
• all of order q ⁿ p divides with q ⁿ 2 ⁸ , 3 ⁶ , 5 ⁵ or 7 ⁴ and p is any prime number other than q ;
• all groups whose order n is not divided by p ² for any prime p (i.e. n is square-free );
• all groups whose order n can be decomposed into at most three prime numbers.

This library was created by Hans Ulrich Besche, Bettina Eick and Eamonn O'Brien.

Individual evidence

1. ↑ In the list of subgroups, the trivial subgroups (the single-element group and the group itself) are not listed.
2. ^ Bertram Huppert : Finite groups I. Springer-Verlag, 1967, chap. I, § 2, sentence 2.10.
3. ^ Bertram Huppert: Finite Groups I. Springer-Verlag (1967), chap. I, § 6, sentence 6.10.
4. ^ Kurt Meyberg: Algebra Part 1. Carl Hanser Verlag, 1980, ISBN 3-446-13079-9 , sentence 2.2.12.
5. ^ Kurt Meyberg: Algebra part 1. Carl Hanser Verlag (1980), ISBN 3-446-13079-9 , example 2.2.11 e.
6. ^ Bertram Huppert: Finite Groups I. Springer-Verlag (1967), chap. I, § 8, sentence 8.10.
7. ↑ The Small Groups library. At: www.gap-system.org .

Web links

• Thomas Keilen: Finite Groups. (PS, German; GZIP ; 202 kB), see § 15: Classification of groups up to order 23.
• Eric W. Weisstein : Finite Group . In: MathWorld (English).
• Detailed classification of the groups up to order 28 (English).

This version was included in the selection of informative lists and portals on August 1, 2007 .