Cycle graph

In group theory , a branch of abstract algebra , the cycle graph represents the various cycles of a group and is particularly useful for visualizing the structure of small, finite groups , but does not play an important role in group theory.

Cycle

A cycle of a group is the set of powers of a given group element , where the n-th power of an element is defined as the n-fold product of itself. In a finite group, a positive power of must result in the neutral element , the smallest power for which this occurs is the number of different elements of the cycle and is called its order . In a cycle graph, the cycles are shown as polygons, the corners of the graph stand for the group elements and edges indicate that the corners of the polygon connected by them belong to the same cycle. ${\ displaystyle a}$ ${\ displaystyle a ^ {n}}$ ${\ displaystyle a}$ ${\ displaystyle a}$ ${\ displaystyle a}$ ${\ displaystyle e}$

Cycles can overlap or, with the exception of the neutral element, have no element in common. The cycle graph shows each cycle of interest as a polygon.

If generates a cycle of order 6 (or in short: has order 6), then is . The set of powers of is the cycle , but does not represent new information because it is contained in the cycle generated by . creates the same cycle as . ${\ displaystyle a}$ ${\ displaystyle a ^ {6} = e}$ ${\ displaystyle a ^ {2}}$ ${\ displaystyle \ {a ^ {2}, a ^ {4}, e \}}$ ${\ displaystyle a}$ ${\ displaystyle a ^ {5}}$ ${\ displaystyle a}$

Therefore only so-called primitive cycles need to be considered, that is, those that are not a subset of another. Each of these cycles is generated by one or more primitive elements . The cycle graph is created by taking the group elements as corners , dragging an edge to a primitive element for each primitive cycle and then connecting them with , with , ... until you get back to the neutral element. ${\ displaystyle e}$ ${\ displaystyle a}$ ${\ displaystyle a}$ ${\ displaystyle a ^ {2}}$ ${\ displaystyle a ^ {2}}$ ${\ displaystyle a ^ {3}}$

If , that is, it has order 2, i.e. is an involution , then this element is connected via two edges . If this is not to be emphasized, only one edge is typically drawn. ${\ displaystyle a ^ {2} = e}$ ${\ displaystyle a}$ ${\ displaystyle e}$

Examples

Cycle graph of the dihedral group

{\ displaystyle D_ {4}}

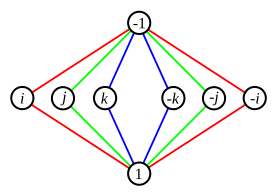
As an example of a cycle graph we consider the dihedral group . The link table is on the left, on the right is the cycle graph with the neutral element : ${\ displaystyle D_ {4}}$ ${\ displaystyle e}$

^O	e	b	a	a ²	a ³	from	a ²b	a ³b
e	e	b	a	a ²	a ³	from	a ²b	a ³b
b	b	e	a ³b	a ²b	from	a ³	a ²	a
a	a	from	a ²	a ³	e	a ²b	a ³b	b
a ²	a ²	a ²b	a ³	e	a	a ³b	b	from
a ³	a ³	a ³b	e	a	a ²	b	from	a ²b
from	from	a	b	a ³b	a ²b	e	a ³	a ²
a ²b	a ²b	a ²	from	b	a ³b	a	e	a ³
a ³b	a ³b	a ³	a ²b	from	b	a ²	a	e

Look at the cycle . The successive powers of can be taken from the link table . The reverse order is also possible, that is, it applies and finally . This applies to all cycles of each group, a cycle can be run through in any direction. ${\ displaystyle \ {e, a, a ^ {2}, a ^ {3} \}}$ ${\ displaystyle a}$ ${\ displaystyle (a ^ {3}) ^ {2} = a ^ {2}, (a ^ {3}) ^ {3} = a}$ ${\ displaystyle (a ^ {3}) ^ {4} = e}$

Cycle graph of the quaternion group

{\ displaystyle Q_ {8}}

Cycles with a non- prime number of elements always have sub-cycles that are not shown in the cycle graph. One might be tempted to draw an edge between and in the cycle graph of group D ₄ , but this does not happen because the cycle of order 2 generated by is part of the larger cycle of order 4 generated by . ${\ displaystyle a ^ {2}}$ ${\ displaystyle e}$ ${\ displaystyle a ^ {2}}$ ${\ displaystyle a}$

As already stated above, two-element cycles are usually only represented by an edge.

If two cycles have a different corner in common, there may be ambiguities about the course of the cycle. To do this, consider the quaternion group , the cycle graph of which is shown opposite. The square of the element in the middle row is −1, where 1 stands for the neutral element in . Here, as shown in the drawing, you can mark cycles with different colors. ${\ displaystyle e}$ ${\ displaystyle Q_ {8}}$ ${\ displaystyle Q_ {8}}$

The inverse of an element can be found in the cycle graph by finding the element in the cycle to which this element belongs that is just as far away from the neutral element when the cycle is reversed.

history

Cycle graphs were studied in the early 1950s by number theorist Daniel Shanks as a means of studying prime residual class groups. Shanks first published this idea in 1962 in the first edition of his book Solved and Unsolved Problems in Number Theory . In this book, Shanks examines which groups have isomorphic cycle graphs and which cycle graphs are planar . In the second edition published in 1978, Shanks writes about his investigation of ideal class groups and the development of the baby step-giant step method :

The cycle graphs have proved to be useful when working with finite Abelian groups; and I have used them frequently in finding my way around an intricate structure, in obtaining a wanted multiplicative relation, or in isolating some wanted subgroup.

German: The cycle graphs have proven useful when working with Abelian groups; and I have often used them to find my way around intricate structures, to maintain sought-after multiplicative relationships, or to isolate some sought-after subgroups.

In Nathan Carter's introductory textbook Visual Group Theory , published in 2009, Zykel groups were used as an educational tool.

Graph properties of certain group families

Certain types of groups have typical cycle graphs:

The cycle graphs of the cyclic groups of the order are -sided regular polygons , each corner stands for a group element. ${\ displaystyle \ mathbb {Z} _ {n}}$ ${\ displaystyle n}$ ${\ displaystyle n}$

Z ₁	Z ₂ = D ₁	Z ₃	Z ₄	Z ₅	Z ₆ = Z ₃ × Z ₂	Z ₇	Z ₈


No. ₉	Z ₁₀ = Z ₅ × Z ₂	No. ₁₁	Z ₁₂ = Z ₄ × Z ₃	Z ₁₃	Z ₁₄ = Z ₇ × Z ₂	Z ₁₅ = Z ₅ × Z ₃	Z ₁₆

Z ₁₇	Z ₁₈ = Z ₉ × Z ₂	Z ₁₉	Z ₂₀ = Z ₅ × Z ₄	Z ₂₁ = Z ₇ × Z ₃	Z ₂₂ = Z ₁₁ × Z ₂	Z ₂₃	Z ₂₄ = Z ₈ × Z ₃

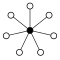
Direct products from : ${\ displaystyle \ mathbb {Z} _ {2}}$

Z ₂	Z ₂² = D ₂	Z ₂³ = D ₂ × D ₁	Z ₂⁴ = D ₂²

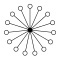
If a prime number , then the cycle graphs of the groups consist of cycles of the order that have the neutral element in common: ${\ displaystyle n}$ ${\ displaystyle (\ mathbb {Z} _ {n}) ^ {m}}$ ${\ displaystyle \ textstyle {\ frac {n ^ {m} -1} {n-1}}}$ ${\ displaystyle n}$

Z ₂² = D ₂	Z ₂³ = D ₂ × D ₁	Z ₂⁴ = D ₂²	Z ₃²

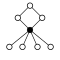
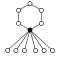
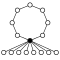
The cycle graphs of the dihedral groups of the order have an n -element cycle and n 2-element cycle : ${\ displaystyle D_ {n}}$ ${\ displaystyle 2n}$

D ₁ = Z ₂	D ₂ = Z ₂²	D ₃	D ₄	D ₅	D ₆ = D ₃ × Z ₂	D ₇	D ₈	D ₉	D ₁₀ = D ₅ × Z ₂

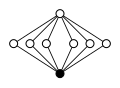
The dicyclic groups of the order have the following cycle graphs: ${\ displaystyle \ mathrm {Dic} _ {n}}$ ${\ displaystyle 4n}$

Dic ₂ = Q ₈	Dic ₃ = Q ₁₂	Dic ₄ = Q ₁₆	Dic ₅ = Q ₂₀	Dic ₆ = Q ₂₄

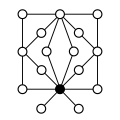
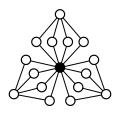
Cycles graphs of other direct products:

Z ₄ × Z ₂	Z ₄ × Z ₂²	Z ₆ × Z ₂	Z ₈ × Z ₂	Z ₄²

Every group of the order is isomorphic to a subgroup of the symmetric group , its cycle graph can therefore be found in the cycle graph of , see the following examples for the . ${\ displaystyle n}$ ${\ displaystyle S_ {n}}$ ${\ displaystyle S_ {n}}$ ${\ displaystyle S_ {4}}$

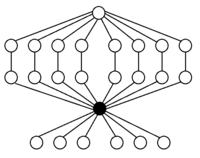A ₄ × Z ₂	S ₃ = D ₃	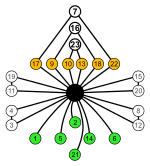S ₄	One of the three D ₄ in S ₄ identical to

literature

S. Skiena: Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica 1990, §4.2.3 Cycles, Stars, and Wheels , pages 144-147
Daniel Shanks: Solved and Unsolved Problems in Number Theory , Chelsea Publishing Company (1978), ISBN 0-8284-0297-3
S. Pemmaraju, S. Skiena: Computational Discrete Mathematics: Combinatorics and Graph Theory in Mathematics Cambridge, England: Cambridge University Press, 2003, §6.2.4 Cycles, Stars, and Wheels pages 248-249

Web links

Eric W. Weisstein : Cycle Graph . In: MathWorld (English).
RJ Mathar: Cycle graph plots of finite groups up to order 36 . 2014.

Individual evidence

^ Sarah Perkins: Commuting Involution Graphs for A˜n, Section 2.2, page 3, first figure . School of Economics, Mathematics and Statistics. 2000. Retrieved January 31, 2016.
↑ Shanks 1978, p. 246
↑ Shanks 1978, p. Xii
↑ Shanks 1978, pp. 83-98, 206-208
^ Nathan Carter (2009): Visual Group Theory , Mathematical Association of America, Classroom Resource Materials ISBN 978-0-88385-757-1

[1] Sarah Perkins: Commuting Involution Graphs for A˜n, Section 2.2, page 3, first figure . School of Economics, Mathematics and Statistics. 2000. Retrieved January 31, 2016.

[2] Shanks 1978, p. 246

[3] Shanks 1978, p. Xii

[4] Shanks 1978, pp. 83-98, 206-208

[5] Nathan Carter (2009): Visual Group Theory , Mathematical Association of America, Classroom Resource Materials ISBN 978-0-88385-757-1