Flux balance analysis

The results of FBA on a prepared metabolic network of the top six reactions of glycolysis. The predicted flux through each reaction is proportional to the width of the line. Objective function in red, constraints on alpha-D-Glucose and beta-D-Glucose import represented as red bars.

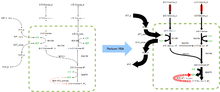
Flux Balance Analysis (FBA) is a mathematical method for analysing metabolism. It does not require knowledge of metabolite concentration or details of the enzyme kinetics of the system. The assumption is made that the system being studied is homeostatic and the technique then aims to answer the question: given some known available nutrients, which set of metabolic fluxes maximises the growth rate of an organism whilst preserving the internal concentration of metabolites?

A notable example of the success of FBA is the ability to accurately predict the growth rate of E. coli when cultured in different conditions. More generally, suitable organisms can be cultivated in media with defined concentrations of nutrients, and their growth rates measured, so that the predictions of FBA can be compared with experiments and the underlying metabolic model corrected accordingly.

A good description of the basic concepts of FBA can be found in the freely available supplementary material to Edwards et al. 2001 which can be found at the Nature website. Further sources include the book "Systems Biology" by B. Palsson dedicated to the subject and a useful tutorial and paper by J. Orth. Many other sources of information on the technique exist in published scientific literature including Lee et al. 2006 and Feist et al. 2008.

Comparison with other techniques

FBA provides a less simplistic analysis than Choke Point Analysis while requiring far less information on reaction rates and a much less complete network reconstruction than a full dynamic simulation would require. In filling this niche, FBA has been shown to be a very useful technique for analysis of the metabolic capabilities of cellular systems.

Choke Point Analysis

Unlike Choke Point Analysis, FBA is a true form of metabolic network modelling because it considers the metabolic network as a single entity (the stoichiometric matrix) at all stages of analysis. This means that network effects, such as chemical reactions in distant pathways affecting each other, can be reproduced in the model. The upside to the inability of choke point analysis to simulate network effects is that it considers each reaction within a network in isolation and thus can suggest important reactions in a network even if a network is highly fragmented and contains many gaps.

Dynamic Metabolic Simulation

Unlike Dynamic Metabolic Simulation, FBA assumes that the internal concentration of metabolites within a system stays constant over time and thus is unable to provide anything other than steady-state solutions. It is unlikely that FBA could, for example, simulate the functioning of a nerve cell. Since the internal concentration of metabolites is not considered within a model, it is possible that an FBA solution could contain metabolites at a concentration too high to be biologically acceptable: a problem that dynamic metabolic simulations would probably avoid. One advantage of the simplicity of FBA over dynamic simulations is that they are far less computationally expensive, allowing the simulation of large numbers of perturbations to the network. A second advantage is that the reconstructed model can be substantially simpler by avoiding the need to consider enzyme rates and the effect of complex interactions on enzyme kinetics.

Model Preparation

A comprehensive guide to creating, preparing and analysing a metabolic model using FBA, in addition to other techniques, was published by Thiele and Palsson in 2010. The key parts of model preparation are: creating a metabolic network without holes, adding constraints to the model and finally adding an objective function (often called the Biomass function), usually to simulate the growth of the organism being modelled.

The Network

The first six reactions in Glycolysis prepared for FBA through the addition of an objective function (red) and the import and export of nutrients (ATP, ADP, BDG, ADG) across the system boundary (dashed green line)

Metabolic networks can vary in scope from those describing the metabolism in a single pathway, up to the cell, tissue or organism. The only requirement of a metabolic network that forms the basis of an FBA-ready network is that it contains no gaps. This typically means that extensive manual curation is required, making the preparation of a metabolic network for flux-balance analysis a process that can take months or years. Software packages such as Simpheny, CellDesigner and MetNetMaker, exist to speed up the creation of new FBA-ready metabolic networks.

Generally models are created in BioPAX or SBML format so that further analysis or visualisation can take place in other software although this not a requirement.

Objective Function

In FBA there are a large number of mathematically acceptable solutions to the steady-state problem $(S{\vec {v}}=0)$ but the ones that are biologically interesting are those that produce the desired metabolites in the correct proportion. The set of metabolites, in the correct proportions, that an FBA model tries to create is called the objective function. When modelling an organism the objective function is generally the biomass of the organism and simulates growth and reproduction. If the biomass function is defined sensibly, or exactly measured experimentally, it can play an important role in making the results of FBA biologically applicable: by ensuring that the correct proportion of metabolites are produced by metabolism and by predicting exact rates of Biomass production for example.

When modelling smaller networks the objective function can be changed accordingly. An example of this would be in the study of the carbohydrate metabolism pathways where the objective function would probably be defined as a certain proportion of ATP and NADH and thus simulate the production of high energy metabolites by this pathway.

Constraints

A key part of FBA is the ability to add constraints to the flux rates of reactions within networks, forcing them to stay within a range of selected values. This lets the model more accurately simulate real metabolism and can be thought of biologically in two subsets; constraints that limit nutrient uptake and excretion and those that limit the flux through reactions within the organism. FBA-ready metabolic models that have had constraints added can be analysed using software such as the COBRA toolbox.

Growth media

Organisms, and all other metabolic systems, require some input of nutrients. Typically the rate of uptake of nutrients is dictated by their availability (a nutrient that isn’t present cannot be absorbed), their concentration and diffusion constants (higher concentrations of quickly-diffusing metabolites are absorbed more quickly) and the method of absorption (such as active transport or facilitated diffusion versus simple diffusion).

If the rate of absorption (and/or excretion) of certain nutrients can be experimentally measured then this information can be added as a constraint on the flux rate at the edges of a metabolic model. This ensures that nutrients that are not present or not absorbed by the organism do not enter its metabolism (the flux rate is constrained to zero) and also means that known nutrient uptake rates are adhered to by the simulation. This provides a secondary method of making sure that the simulated metabolism has experimentally verified properties rather than just mathematically acceptable ones. In mathematical terms, the application of constraints can be considered to reduce the solution space of the FBA model.

Internal constraints

In addition to constraints applied at the edges of a metabolic network, constraints can be applied to reactions deep within the network. These constraints are normally usually simple; they may constrain the direction of a reaction due to energy considerations or constrain the maximum speed of a reaction due to the finite speed of all reaction in nature.

Mathematical Description

A biological network can be thought of as a set of nodes (compounds) connected by directional edges (reactions) and therefore represented as a matrix. The properties of this matrix are well known and thus a biological problem becomes amenable to computational analysis. A real biological system is extremely complex which in turn leads to problems measuring enough parameters to define the system and in some cases requiring a huge amount of computing time to perform simulations. Flux-balance analysis simplifies the representation of the biological system, requiring fewer parameters (such as enzyme kinetic rates, compound concentrations and diffusion constants) and greatly reduces the computer time required for simulations.

A Simple Example

A simple reaction network with two reactions and three compounds

The concentrations of all the metabolites and the fluxes through all the reactions in this simple system can be represented by the following three differential equations.

${d[C]_{1} \over dt}=v_{2}-v_{1}$

${d[C]_{2} \over dt}=v_{1}-v_{2}$

${d[C]_{3} \over dt}=-v_{1}$

Solving this system of differential equations is not difficult in this case but quickly becomes computationally expensive as the number of differential equations in the system rises. There is a second obstacle to solving this system; the reaction rates, $v_{1},v_{2}\,$ and $v_{3}\,$ are themselves dependent on a number of factors generally taken from the Michelis-Menton kinetic theory, including the kinetic parameters of the enzymes catalysing the reactions and the concentration of the metabolites themselves. Isolating enzymes from living organisms and measuring their kinetic parameters is a difficult task, as is measuring the internal concentrations, and diffusion constants, of metabolites within an organism. For this reason the differential equation approach to modelling metabolism becomes extraordinarily difficult and beyond the current scope of science for all but the most studied organisms (link to Heinemann E. Coli paper with all internal fluxes measured and Manchester yeast paper with internal fluxes measured).

The Power of Homeostasis

Much of the power of flux-balance analysis comes from applying the principle of homeostasis to the problem. Since the internal concentrations of metabolites within a biological system remain more or less the same over time we can apply the homeostatic condition that,

${d[C]_{1} \over dt}={d[C]_{2} \over dt}={d[C]_{3} \over dt}=0$

Or in the general case,

${d[C]_{i} \over dt}=0$

And thus simplify the problem to one of simply balancing the fluxes within the system, hence the name flux-balance analysis.

$v_{2}-v_{1}=v_{1}-v_{2}=-v_{1}\,$

This set of equations is now much easier to solve, although in this case the only solution is the null solution $v_{1}=v_{2}=0\,$.

The Stoichiometric Matrix

An example stoichiometric matrix for a network representing the top of glycolysis and that same network after being prepared for FBA.

The representation of the equations above can be generalised to any similar biological network and represented in a more powerful manner by using matrices. The stoichiometric matrix for the simple set of reactions above is,

${\mathbf {S}}={\begin{bmatrix}-1&1\\-1&0\\1&-1\\\end{bmatrix}}$

Confusingly, the stoichiometric matrix is often referred to in chemistry with the letter $\scriptstyle {\mathbf {N}}$ but within the field of systems biology is almost always referred to as $\scriptstyle {\mathbf {S}}$. Both letters are exactly equivalent. At this stage it is useful to define a vector $\textstyle {\vec {v}}$ where each component of the vector represents the rate (flux through) its respective reaction within the stoichiometric matrix

${\vec {v}}={\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}$

Multiplying this matrix, $\scriptstyle {\mathbf {S}}$, with $\textstyle {\vec {v}}$, is completely equivalent to the equations derived directly from the reaction diagram,

${\begin{bmatrix}-1&1\\-1&0\\1&-1\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\end{bmatrix}}={\begin{bmatrix}-v_{1}+v_{2}\\v_{1}-v_{2}\\-v_{1}\\\end{bmatrix}}={\begin{bmatrix}{d[C]_{1} \over dt}\\{d[C]_{2} \over dt}\\{d[C]_{3} \over dt}\\\end{bmatrix}}$

Applying the homeostatic condition then gives us,

${\begin{bmatrix}-1&1\\-1&0\\1&-1\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\end{bmatrix}}={\begin{bmatrix}-v_{1}+v_{2}\\v_{1}-v_{2}\\-v_{1}\\\end{bmatrix}}={\begin{bmatrix}{d[C]_{1} \over dt}\\{d[C]_{2} \over dt}\\{d[C]_{3} \over dt}\\\end{bmatrix}}={\begin{bmatrix}0\\0\\0\\\end{bmatrix}}$

In the general case we can write,

${\mathbf {S}}\,{\vec {v}}=0$

Or often confusingly, given the different nature of the $\cdot$ when referring to the vector dot product, but identically as,

${\mathbf {S}}\cdot {\vec {v}}=0$

With the single $0$ representing the null vector,

$0={\begin{bmatrix}0\\.\\.\\.\\0\\\end{bmatrix}}$.

The results of FBA can be represented identically as a vector of fluxes, or by weighting the lines representing the reactions according to the flux they carry.

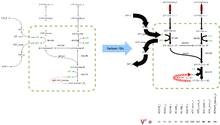
This general operation is called taking the Null Space of the stoichiometric matrix $\scriptstyle {\mathbf {S}}$ and the technique is valid for all stoichiometric matrices, not just the small example here. Since a typical stoichiometric matrix contains many more metabolites than reactions ($m<n\,$) and the majority of reactions are linearly independent there are many vectors $\textstyle {\vec {v}}$ that satisfy the equation and thus span the Null Space of $\scriptstyle {\mathbf {S}}$.

Application to the Biology of the System

The analysis of the null space of matrices is common within linear algebra and many software packages such as Matlab and Octave can help with this process. Nevertheless, knowing the null space of ${\mathbf {S}}$ only tells us all the possible collections of flux vectors (or linear combinations thereof) that balance fluxes within the biological network. Flux-balance analysis has two further aims, to accurately represent the biology limits of the system and to return the flux distribution closest to that naturally occurring within the target system/organism.

Constraints

The stoichiometric matrix is almost always underdetermined meaning that the solution space to $\textstyle {\mathbf {S}}\,{\vec {v}}=0$ is very large. The size of the solution space can be reduced, and made more reflective of the biology of the problem through the application of certain constraints on the solutions.

Thermodynamic

In principle all reactions are reversible however in practise many reactions effectively occur in only one direction. This can be because of a significantly higher concentration of reactants compared to the concentration of the products of the reaction but is more often because the products of a reaction have a much lower free energy than the reactants and therefore the forward direction of a reaction is massively favoured. For ideal reactions,

$-\infty <v_{i}<\infty$

For certain reactions a thermodynamic constraint can be applied implying direction (in this case forward)

$0<v_{i}<\infty$

Realistically the flux through a reaction cannot be infinite which implies that,

$0<v_{i}<v_{\textrm {max}}\,$

Measured Flux Rates

Certain flux rates can be measured experimentally ($v_{i,m}\,$) and the fluxes within a metabolic model can be constrained, within some error ($\epsilon \,$), to ensure these known flux rates are accurately reproduced in the simulation.

$v_{i,m}-\epsilon <v_{i}<v_{i,m}+\epsilon \,$

Flux rates are most easily measured for nutrient uptake at the edge of the network but measurements of internal fluxes are possible, generally using radioactively labelled or NMR visible metabolites.

Optimisation (the Objective/Biomass function)

Even after the application of constraints there is usually a large number of possible solutions to the flux-balance problem. If an optimisation goal is defined, linear programming can be used to find a single optimal solution. The most common biological optimisation goal for a whole organism metabolic network would be to choose the flux vector ${\vec {v}}$ that maximises the flux through a biomass function composed of the constituent metabolites of the organism placed into the stoichiometric matrix and denoted $v_{\textrm {biomass}}$ or simply $v_{b}$

$\max _{\vec {v}}\ v_{b}\qquad {\textrm {s.t.}}\qquad {\mathbf {S} }\,{\vec {v}}=0$

In the more general case any reaction be defined and added defined as a biomass function with either the condition that it be maximised or minimised if a single “optimal” solution is desired. Alternatively, and in the most general case, a vector ${\vec {c}}$ can be defined which defines the weighted set of reactions that the linear programming model should aim to maximise or minimise,

$\max _{\vec {v}}\ {\vec {v}}\cdot {\vec {c}}\qquad {\textrm {s.t.}}\qquad {\mathbf {S}}\,{\vec {v}}=0$

In the case of there being only a single separate biomass function/reaction within the stoichiometric matrix ${\vec {c}}$ would simplify to all zeroes with a value of 1 (or any non-zero value) in the position corresponding to that biomass function. Where there were multiple separate objective functions ${\vec {c}}$ would simplify to all zeroes with weighted values in the positions corresponding to all objective functions.

Simulating Perturbations

An example of a non lethal gene deletion in a sample metabolic network with fluxes shown by the weight of the reaction lines as calculated by FBA. Here the flux through the objective function is halved but is still present.

An example of a lethal gene deletion in a sample metabolic network with fluxes shown by the weight of the reaction lines as calculated by FBA. Here there is no flux through the objective function, simulating that the pathway is no longer functional.

FBA is not computationally intensive, taking on the order of seconds to calculate optimal fluxes for biomass production for a simple organism (around 1000 reactions). This means that the effect of deleting reactions from the network and/or changing flux constraints can be sensibly modelled on a single computer.

Single Reaction Deletion

A frequently used technique to search a metabolic network for reactions that are particularly critical to the production of biomass. By removing each reaction in a network in turn and measuring the predicted flux through the biomass function, each reaction can be classified as either essential (if the flux through the biomass function is substantially reduced) or non-essential (if the flux through the biomass function is unchanged or only slightly reduced).

Reaction Inhibition

The effect of inhibiting a reaction, rather than removing it entirely, can be simulated in FBA by restricting the allowed flux through it. The effect of an inhibition can be classified as lethal or non-lethal by applying the same criteria as in the case of a deletion where a suitable threshold is used to distinguish “substantially reduced” from “slightly reduced”. Generally the choice of threshold is arbitrary but a reasonable estimate can be obtained from growth experiments where the simulated inhibitions/deletions are actually performed and growth rate is measured.

Interpreting Results

The utility of reaction inhibition and deletion analyses is most clear if a gene-protein-reaction matrix has been assembled for the network being studied with FBA. If this has been done then information on which reactions are essential can be converted into information on which genes are essential (and thus what gene defects may cause a certain disease) or which proteins/enzymes are essential (and thus what enzymes are the most promising drug targets in pathogens).

Reaction Deletion in Pairs

An extension of single reaction deletions are double reaction deletions where all possible pairs of reactions are deleted. This can be useful when looking for drug targets as it allows the simulation of multi-target treatments, either by a single drug with multiple targets or by drug combinations.

Growth Media Modification

FBA has also been used to simulate the effect on growth rate of changes in the growth media of the metabolic system being studied. In E. coli the predicted growth rates of bacteria in varying media have been shown to correlate well with experimental results as well as to define precise minimal media for the culture of Salmonella typhimurium.