Rhombic triacontahedron

Rhombic triacontahedron
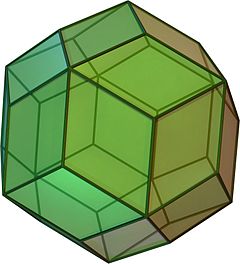Click on picture for large version. Click here for spinning version.
Type	Catalan
Face polygon	rhombus
Faces	30
Edges	60
Vertices	32 = 20 + 12
Face configuration	V3.5.3.5
Symmetry group	icosahedral (Ih)
Dual polyhedron	icosidodecahedron
Properties	convex, face-uniform, edge-uniform, zonohedron

In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron. The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio, φ, so that the acute angles on each face measure 2 tan⁻¹(1/φ) = tan⁻¹(2), or approximately 63.43°. A rhombus so obtained is called a golden rhombus.

Being the dual of an Archimedean polyhedron, the rhombic triacontahedron is face-uniform, meaning the symmetry group of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic triacontahedron is also somewhat special in being one of the nine edge-uniform convex polyhedra, the others being the five Platonic solids, the cuboctahedron, the icosidodecahedron, and the rhombic dodecahedron.

The rhombic triacontahedron forms the (hull of) the projection of a 6-dimensional hypercube to 3 dimensions.

Uses of rhombic triacontahedra

Danish designer Holger Strøm used the rhombic triacontahedron as a basis for the design of his buildable lamp IQ-light™. (IQ for "Interlocking Quadrilaterals")

In some roleplaying games, and for elementary school uses, the rhombic triacontahedron is used as the "d30" thirty-sided die.

See also

• Truncated rhombic triacontahedron

External links

• Rhombic Triacontahedron – from MathWorld
• Virtual Reality Polyhedra – The Encyclopedia of Polyhedra
• IQ-light™–Danish designer Holger Strøm´s lamp