Trapezoidal rule

The function f(x) (in blue) is approximated by a linear function (in red).

Illustration of the composite trapezium rule (with a non-uniform grid).

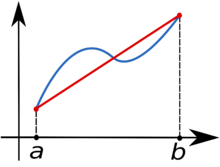
In mathematics, the trapezium rule (the British term) or trapezoidal rule (the American term) is a way to approximately calculate the definite integral

$\int _{a}^{b}f(x)\,dx.$

The trapezium rule works by approximating the region under the graph of the function $f(x)$ by a trapezium and calculating its area. It follows that

$\int _{a}^{b}f(x)\,dx\approx (b-a){\frac {f(a)+f(b)}{2}}.$

To calculate this integral more accurately, one first splits the interval of integration $[a,b]$ into n smaller subintervals, and then applies the trapezium rule on each of them. One obtains the composite trapezium rule:

$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{n}}\left[{f(a)+f(b) \over 2}+\sum _{k=1}^{n-1}f\left(a+k{\frac {b-a}{n}}\right)\right].$

This can alternatively be written as:

$\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{2n}}\left(f(x_{0})+2f(x_{1})+2f(x_{2})+\cdots +2f(x_{n-1})+f(x_{n})\right)$

where

$x_{k}=a+k{\frac {b-a}{n}},$ for $k=0,1,\dots ,n$ (one can also use a non-uniform grid).

The trapezium rule is one of a family of formulas for numerical integration called Newton–Cotes formulas. Simpson's rule is another, often more accurate, member of the same family. Simpson's rule and other like methods can be expected to improve on the trapezium rule for functions which are twice continuously differentiable; however for rougher functions the trapezium rule is likely to prove preferable. Moreover, the trapezium rule tends to become extremely accurate when periodic functions are integrated over their periods, a fact best understood in connection with the Euler–Maclaurin summation formula. For non-periodic functions, however, methods with unequally spaced points such as Gaussian quadrature and Clenshaw–Curtis quadrature are generally far more accurate.

An advantage of the trapezium rule is that the sign of the error of the approximation is easily known. An integral approximated with this rule on a concave-up function will be an overestimate because the trapezoids include all of the area under the curve and extend over it. Using this method on a concave-down function yields an underestimate because area is unaccounted for under the curve, but none is counted above. If the interval of the integral being approximated includes an inflection point, then the error is harder to identify.

See also

• Simpson's rule
• Romberg integration
• Newton–Cotes formulas

References

• Burden, Richard L. (2000). Numerical Analysis (7th Ed. ed.). Brooks/Cole. ISBN 0-534-38216-9. {{cite book}}: |edition= has extra text (help); Unknown parameter |coauthors= ignored (|author= suggested) (help)
• Trapezoidal Rule of Integration - Notes, PPT, Mathcad, Maple, Mathematica, Matlab at Holistic Numerical Methods Institute

External links

• Trapezoidal Rule for Numerical Integration