Diagonal functor

In the mathematical subfield of category theory , the diagonal functor is a functor that allows a category to be embedded in the category of functors for any non-empty ( small ) category . The name comes from the fact that for a discrete with two elements the diagonal functor is just the mapping . ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}^{\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle {\mathcal {C}}\to {\mathcal {C}}\times {\mathcal {C}},u\mapsto (u,u)}$

Definition and functoriality

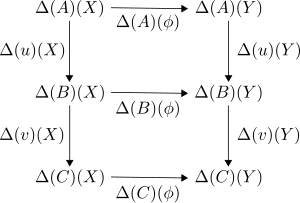
Be a category and a small category. Then the diagonal functor is defined as a mapping that assigns a natural transformation to each morphism , given that they assign each object and thus each morphism to the morphism . For an object there is obviously a functor. In order to see that is actually a functor, consider the concatenation of natural transformations for morphisms and from the category and , by definition, this results in the following commutative diagram for each : ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle \Delta }$ ${\displaystyle u\in {\mathcal {C}}}$ ${\displaystyle \Delta (u)\in {\mathcal {C}}^{\mathcal {D}}}$ ${\displaystyle \Delta (u)}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle u}$ ${\displaystyle A\in {\mathcal {C}}}$ ${\displaystyle \Delta (A)}$ ${\displaystyle \Delta }$ ${\displaystyle u\colon A\to B}$ ${\displaystyle v\colon B\to C}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \Delta (u)}$ ${\displaystyle \Delta (v)}$ ${\displaystyle \phi \colon X\to Y}$ ${\displaystyle {\mathcal {D}}}$

This is nothing more than:

This corresponds to the natural transformation , which proves that . For non-empty is obviously injective , i.e. embedded in the corresponding functor category . Under a certain condition is also full : be natural transformation, i. i.e. that for each in the diagram ${\displaystyle \Delta (uv)}$ ${\displaystyle \Delta (uv)=\Delta (u)\Delta (v)}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle \Delta }$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \Delta }$ ${\displaystyle \alpha \colon \Delta (A)\to \Delta (B)}$ ${\displaystyle \phi \colon X\to Y}$ ${\displaystyle {\mathcal {D}}}$

commutes (because and ). Which means nothing else than that whenever a morphism exists between and . If the category as a graph construed weakly connected is, is so constant and thus the image of , which is full. For example, this is true for an arrow category or, more generally, for with a start or end object, but not for a product for discrete with at least two elements. ${\displaystyle \Delta (A)(\phi )=A}$ ${\displaystyle \Delta (B)(\phi )=B}$ ${\displaystyle \alpha (X)=\alpha (Y)}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle \alpha }$ ${\displaystyle \Delta }$ ${\displaystyle \Delta }$ ${\displaystyle {\mathcal {C}}^{\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle {\mathcal {C}}^{\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}}$

Connection with limits

A cone with respect to a functor is nothing more than an object in provided with a natural transformation from to . A Limes of is a special cone, namely a - universal solution for . Dual to this is a Kolimes of a special Kokegel, namely a -universal solution for . If has a right adjoint functor , then it is completely up with respect to limits , the converse also applies. This adjoint functor is precisely the Limes functor . Correspondingly, the Kolimes functor (if it exists) is left adjoint to the diagonal functor. ${\displaystyle F\colon {\mathcal {D}}\to {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \Delta (A)}$ ${\displaystyle F}$ ${\displaystyle F}$ ${\displaystyle \Delta }$ ${\displaystyle F}$ ${\displaystyle F}$ ${\displaystyle \Delta }$ ${\displaystyle F}$ ${\displaystyle \Delta }$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {D}}}$

The diagonal functor is continuous , i.e. i.e., it receives all limits that exist in. He also receives all Kolimites. ${\displaystyle {\mathcal {C}}}$

literature

• Saunders Mac Lane: Categories for the Working Mathematician . 2nd Edition. Springer , New York 1998, ISBN 0-387-98403-8 .
• Dieter Pumplün: Elements of the category theory . 1st edition. Spektrum Akademischer Verlag , Heidelberg 1999, ISBN 3-86025-676-9 .

Web links

• diagonal functor , entry in the nLab . (English)

Individual evidence

1. ↑ Pumplün, pp. 105-106
2. ^ Mac Lane, p. 233
3. ↑ Pumplün, p. 169