k-opt heuristic

The k-opt heuristics are a class of algorithms for approximating the problem of the traveling salesman (TSP) . The k-opt heuristics belong to the post-optimization algorithms (ger .: After optimization) , which are characterized in that they improve a solution already found. The basic idea is to remove edges from a given tour and replace them with other edges so that a tour results again. If the new tour is shorter than the old one, it is used as the new solution. ${\displaystyle k}$ ${\displaystyle k}$

Procedure

Post-optimization in the PdH consists in modifying a round tour found by chance or heuristics in such a way that the sum of the edge evaluations along the tour is reduced. The k-Opt method is characterized by the fact that it removes a certain number of edges from the current solution in order to then insert new edges that close the gaps that have arisen.

The k-opt heuristics use the local neighborhood search method . The neighborhood to a given solution f is defined as the set of all solutions that can be obtained by certain fixed changes to f . In the case of the k-opt heuristic, a k-swap neighborhood is defined as the set of all valid solutions that arise when k edges are removed from f and then k new edges are inserted. To ensure the validity of the solution, the new edges must close the circular route. ${\displaystyle N,(f)}$ ${\displaystyle N_{k},(f)}$

structure

The following scheme characterizes the class of k-opt heuristics:

1. Choose a round trip f (by chance or a heuristic)
2. As long as there is a better solution g in the neighborhood are ${\displaystyle N_{k},(f)}$

   • Choose g as the new f

3. Return f

Algorithms

The various algorithms of the k-Opt class are characterized by several properties. On the one hand, the choice of the strategy according to which a new g is determined is important. Another factor is the decision on a method for determining the starting solution f . Finally, the choice of the parameter k has a great influence on the time complexity of the algorithm.

In the following some properties are mentioned that have become established in connection with k-opt heuristics:

Strategies

• First improvement (English: first improvement)
  • Selects the first best solution g of which is better than f ${\displaystyle N_{k},(f)}$
• Steepest descent (English: steepest descent)
  • Selects the solution g of which offers the greatest improvement ${\displaystyle N_{k},(f)}$

Algorithms for determining the starting solution

• Farthest insertion
• Nearest insertion
• Christofides' algorithm

Values ​​for k

Paint the intersecting edges and replace them with the two green ones.

• k = 2
  • The simplest case. Two edges are removed and reinserted crosswise.

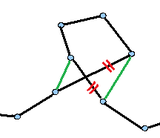
If the triangle inequality is present , which is a practical prerequisite, it can be shown that the result of the 2-opt heuristic is a crossover-free tour. If there is a crossover, you can, as indicated in the adjacent sketch, remove the crossed edges and replace them with two others that do not cross one another. Because of the triangle inequality, you get a real improvement.

• k = 3
  • According to Lin (1965) the case that achieves the best results in relation to the time required.

Algorithms

The best known k-opt algorithm is that of S. Lin and BW Kernighan (1973). It works very efficiently in practice, but in individual cases it can have exponential time complexity . What is special about the Lin-Kernighan algorithm is that it works with a variable k-value, which is determined anew in each iteration.

literature

• Dieter Jungnickel : Graphs, Networks and Algorithms. Springer, Berlin et al. 1999, ISBN 3-540-63760-5 , ( Algorithms and computation in mathematics 5), p. 444ff.
• S. Lin: Computer solutions for the traveling salesman problem. In: The Bell system technical journal 44, 1965, ISSN  0005-8580 , pp. 2245-2269.
• S. Lin, BW Kernighan : An effective heuristic algorithm for the traveling salesman problem. In: Operations research 31, 1973. pp. 489-516.