Salesman Problem

The Traveling Salesman Problem (also messenger problem , traveling salesman problem , Engl. Traveling Salesman Problem , or Traveling Salesperson Problem (TSP)) is a combinatorial optimization problem of Operations Research and theoretical computer science . The task is to choose a sequence for visiting several places so that no station except the first is visited more than once, the entire travel distance of the traveling salesman is as short as possible and the first station is the same as the last station.
Since its first mention as a mathematical problem in 1930, many researchers have dealt with it and developed and tested new optimization methods that are currently used for other optimization problems. Today, a multitude of heuristic and exact methods are available with which even difficult cases with several thousand cities can be optimally solved.
The traveling salesman problem occurs in its pure form in many practical applications, for example in tour planning , in logistics or in the design of microchips . More often it occurs, however, on as a problem, such as in the distribution of goods in planning tours of a customer or breakdown service or the genome sequencing . The terms “city” and “distance” are not to be taken literally, rather the cities represent customers to be visited, boreholes or DNA strands, while distance stands for travel time, costs or the degree of correspondence between two DNA strands. In many practical applications, additional conditions such as time windows or limited resources must also be observed, which makes solving the problem considerably more difficult.
The traveling salesman problem is an NP hard problem. Under the previously unproven assumption that the complexity classes P and NP are different, it is therefore true that there is no algorithm that determines a shortest round trip in polynomial worst-case runtime .
history
When the traveling salesman problem was first scientifically investigated is unclear. A handbook for traveling salesmen is known from 1832 (title: The traveling salesman - how he should be and what he has to do in order to receive orders and to be certain of a happy success in his business - from an old commis-voyageur ), in which the problem is mentioned but not treated mathematically. It suggests example tours for some regions in Germany and Switzerland .
The Icosian Game by William Rowan Hamilton from the 19th century, in which the task was to find tours between 20 nodes in a graph, can be seen as the forerunner of the problem . The first explicit mention as a mathematical optimization problem seems to be traced back to Karl Menger , who formulated this in 1930 in a mathematical colloquium in Vienna:
"We call the messenger problem (because this question can be solved in practice by every postman, incidentally also by many travelers) the task of finding the shortest path connecting the points for a finite number of points whose pairwise distances are known."
Soon afterwards, the now common designation Traveling Salesman Problem was introduced by Hassler Whitney of Princeton University .
In addition to the simple definition and comprehensibility of the task, the traveling salesman problem is characterized by the fact that determining good solutions is comparatively easy, while finding a provably optimal solution is very difficult. Therefore, the study of this problem has been less motivated by direct applications since the second half of the 20th century - it serves as a kind of playground for the development of optimization methods.
Many of today's standard methods of integral linear optimization , such as cutting plane methods , branch-and-cut and various heuristic approaches, were developed and tested using the TSP as an example.
Since the 1950s the traveling salesman problem gained popularity in Europe as well as in the USA . Outstanding contributions were made by George Dantzig , Delbert Ray Fulkerson and Selmer M. Johnson , who in 1954 at the RAND Corporation Institute in Santa Monica developed the first formulation of the problem as an integer linear program as well as a cutting plane method to solve it. They calculated a tour for a specific round trip problem (a so-called instance ) with 49 cities and proved that there is no shorter tour. In the 1960s and 1970s, many interdisciplinary research groups dealt with applications of the problem in computer science , economics , chemistry and biology, among others .
Richard M. Karp proved in 1972 the NP-completeness of the Hamilton circle problem , from which the NP-equivalence of the TSP can easily be derived. In doing so, he provided a theoretical justification for the difficulty in solving this problem in practice.
Greater progress was made in the late 1970s and 1980s, when Martin Grötschel , Manfred Padberg , Giovanni Rinaldi and others optimally solved a number of problem instances with up to 2,392 cities with new cutting levels and a branch-and-cut method.
An algorithm described independently by Nicos Christofides and Anatoli I. Serdyukov in 1976 resulted in a round trip that is a maximum of half longer than the optimal tour.
In the 1990s, David Applegate , Robert Bixby , Vašek Chvátal, and William Cook began developing the Concorde program , which helped set many solution records. In 1991, Gerhard Reinelt provided the TSPLIB, a collection of standardized test instances of varying difficulty, with which many research groups could compare their results. In 2006 Cook and others calculated a provably shortest tour through 85,900 cities of a layout problem for integrated circuits , which is the largest optimally solved TSPLIB instance to date. For other instances with millions of cities, they used additional decomposition techniques to determine tours whose length can be proven to be less than 1% from the optimum.
In 2014, András Sebö from the University of Grenoble and Jens Vygen from the University of Bonn set a new record in the field of heuristics with a guarantee of quality with an algorithm that has a polynomial running time : Their new algorithm , called nice-ears decomposition , determines the solutions of the graph -TSP that are at most 1.4 times as long as the optimal round trip route, which is a new record.
Mathematical description
Modeling as a graph
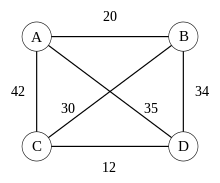
So that mathematical methods can be used for the solution, a real situation must first be represented by a simple model . The traveling salesman's problem can be modeled with the help of a graph , that is, with nodes and edges . (: A to D in the figure) the cities, while each edge The nodes represent between two nodes and a link between these cities describes. For each edge there is a length (in the picture: 20, 42, ...) which, depending on the context, can be interpreted as the geographical length of a connection, as a travel time or as the cost of a trip between two cities. A tour (also called a Hamilton circle ) is a circle in this graph that contains every node exactly once. The aim is to find the shortest possible tour.
In order to simplify the investigation of the problem and to ensure that there is a tour, it is usually assumed that the graph is complete , i.e. that there is always an edge between every two nodes. This can be achieved by inserting an artificial, very long edge wherever there is no edge. Due to its long length, such a ridge will never appear in a shortest tour, unless there is no tour otherwise.
Depending on the properties of the edge weights, different special cases of the problem are distinguished, the most important of which are the symmetrical and the metric TSP.
Asymmetrical and symmetrical TSP
With the general asymmetrical TSP , the edges can have different lengths in the back and forth direction , so that this problem has to be modeled with the help of a directed graph . So it is not enough just to speak of the connection between two nodes and their length; the direction must also be specified.
In the symmetrical TSP, on the other hand, the edge lengths are identical in both directions for all pairs of nodes . H. it applies . As a consequence, every tour is the same length in both directions. The symmetry halves the number of possible tours. A symmetric TSP is usually modeled with the help of an undirected graph (as in the picture). A traveling salesman problem between real cities can be asymmetrical or symmetrical, depending on whether, for example, through construction sites or one-way streets, the journey in one direction takes longer than in the other or not. Likewise, the journey on water or in the air could be exposed to different currents.
Metric TSP
A symmetrical TSP is called metric if its edge lengths also satisfy the triangle inequality . This clearly means that detours are not worthwhile because the direct connection from to is never longer than the route from to via a third node :
Such edge lengths define a pseudometric on the set of nodes, i.e. a distance measure that fulfills the conditions intuitively expected from a distance. Several distance functions that occur frequently in practice are pseudometrics, i.e. they satisfy the triangle inequality:
- the Euclidean metric of the Euclidean TSP ,
- the Manhattan metric (also known as the city block metric) of the rectilinear TSP , in which the distance between two nodes of a grid-shaped graph (such as the Manhattan street network) is the sum of the distances in the x and y directions,
- or the maximum metric , in which the distance between two nodes of a grid-shaped graph is the maximum of the distances in the x or y direction.
The last two metrics are used, for example, when drilling circuit boards , where a drill that has to process a specified number of holes in the shortest possible time can be moved independently in both dimensions in order to get from one hole to the next. The Manhattan metric corresponds to the case that the movement takes place in both directions one after the other, while with the maximum metric both movements take place at the same time and the total time is determined by the longer distance in the x or y direction.
A non-metric TSP can be present, for example, when the duration of a trip is to be minimized and different means of transport are possible on different routes. A detour by plane can be faster than a direct connection by car.
If in the practical planning problem it is permissible to visit places several times, the symmetrical TSP can be reduced to the metric TSP. For this purpose, the round trip problem is considered on the so-called distance graph . This has the same set of nodes as the original graph and is also complete . The edge lengths between two nodes and in the distance graph correspond to the length of a shortest - path between these nodes in the original graph. The values defined in this way always satisfy the triangle inequality, and each tour in the distance graph corresponds to a tour with possible node repetitions in the original graph.
If it is not permissible to visit places more than once, any TSP can also be reduced to a metric TSP by increasing each edge length by the same nonnegative constant: A constant can always be found that is large enough for all To fulfill node triples. In the case of heuristics that guarantee a maximum deviation from the optimum, this procedure naturally increases the deviation factor of the original task.
Formulation as an integral linear program
One approach to solving the problem is to formulate it as an integer linear program in which the decisions are described by variables and the conditions by linear inequalities . There are several possible variants for this. A modeling for the symmetrical TSP with node set is to be presented here as an example . For each edge a binary variable is introduced which indicates for a given tour whether the edge is included in this tour ( ) or not ( ). Each tour can be specified in this way by specifying the associated variable values, but not every 0-1 assignment of the variable values defines a tour. The conditions for a variable assignment to define a tour can be expressed by linear inequalities, which are presented below.
Each node must be connected to the rest of the nodes via exactly two touring edges, namely by an inward and an outward edge:
for everyone . In the sum , each summand is either 1 (included in the tour) or 0 (not included). The sum therefore counts exactly the number of edges of the tour that have the node as an end node. It must have the value 2, since an edge must lead in and out. The picture on the right shows a node with incoming and outgoing edges, with the touring edges being marked in bold. At the edges are the values that contribute to the sums mentioned above.
The above degree conditions are not only met by tours, but also by variable assignments that describe several separate circles (so-called short cycles ), with each node being contained in exactly one circle (see figure). To rule out such a thing, short cycle inequalities (also called subtour elimination conditions) have to be fulfilled. These constraints, introduced by Dantzig, Fulkerson and Johnson in 1954 as loop conditions , state that every node set that is neither empty nor contains all nodes must be connected to the remaining nodes by at least two edges of the tour:
for all sets of nodes with . The sum counts all edges of the tour between one node and another node . To avoid redundant inequalities, one can restrict oneself to node sets with at least two and at most nodes. The picture to the edges again with drawn in bold, while the remaining edges of the value have. Adding condition (2) for the set of nodes , which consists of the three nodes on the left, would ensure that S must be connected to the three nodes on the right by at least two tour edges, thus excluding the two short cycles shown. The number of Dantzig, Fulkerson and Johnson subtour elimination conditions is . An alternative representation of the constraints for avoiding subtours published by Miller, Tucker and Zemlin in 1960 manages with only constraints by introducing new variables that indicate the order of the places visited . However, due to the binary nature of the TSP, even with the formulation according to Miller, Tucker and Zemlin , the TSP remains NP-difficult .
Since every vector with entries from 0 and 1 that fulfills all these inequalities defines a valid round trip, the salesman's reformulated problem arises: Find
Since the variables only take on the values 0 or 1, the sum adds up exactly the lengths of the edges that are contained in the tour.
The number of inequalities of type (2) grows exponentially with the number of cities, since almost each of the subsets of nodes defines an inequality. This problem can, however, be circumvented with the help of cutting plane methods, in which these inequalities are only added when they are actually needed. Geometrically, every linear equation can be interpreted as a hyperplane in the space of the variables. The set of admissible solutions forms a polytope in this space, i.e. a multi-dimensional polygon, the exact shape of which depends on the costs and is mostly unknown. However, it can be shown that most of the conditions (1) and (2) define facets of the TSP polytope, that is, side surfaces of the polytope with the highest possible dimension. This makes them one of the strongest linear inequalities that can be used to describe a tour. There are many other facets, but the associated inequalities are only known in a few cases. Although (1) and (2), together with the restriction to 0/1 vectors, fully model the problem, such additional inequalities can be added to the formulation within a branch-and-cut method to identify certain LP solutions with non-integer Exclude coordinates (see section Exact solution methods ).
Algorithmic Complexity
Since the traveling salesman can choose from the cities he has not yet visited at every step, there are possible tours for an asymmetrical and tours for a symmetrical TSP (with ). The size of the search area depends on the number of cities in an over-exponential manner.
The traveling salesman problem is NP-equivalent for both the general and symmetric or metric cases . Under the generally assumed but so far unproven assumption that the complexity classes P and NP are different (see P-NP problem ), it follows that there is no deterministic Turing machine that can solve the problem for each instance in polynomial running time with respect to the number of cities solves.
It is also known that under the assumption P NP for the general problem of the traveling salesman there can be no polynomial time algorithm which basically calculates a solution for any polynomial whose value deviates from the optimum value by at most one factor .
However, approximation algorithms can be specified for the metric TSP that provide a solution in polynomial runtime that is at most twice ( minimum spanning tree approach ) or at most 1.5 times ( Christofides algorithm ) as long as the optimal solution (see below ). No polynomial time algorithm with a better quality guarantee than 1.5 is known. A polynomial time algorithm with quality guarantee 8/7 is known for the restriction to distances 1 and 2. Assuming P NP there is an (unknown) constant , so that no polynomial time algorithm can exist for the metric TSP that guarantees the quality , as Karpinski, Lampis and Schmied 2013 showed. The corresponding best known constant for the Graph TSP is . Arora (1996) and Mitchell (1996) independently gave a polynomial approximation scheme (PTAS) for the Euclidean TSP.
Solution method
The known solution methods are divided into two groups, which can be combined with one another. Exact solution procedures will always find a provable optimal solution - assuming any length of time. Heuristic methods often find good solutions in a short time, but in general they can be as bad as you want. For the metric TSP there are polynomial heuristics , the solutions of which are generally at most 1.5 or 2 times longer than a shortest round trip.
Exact solution methods
The traveling salesman problem can be solved exactly by calculating the distances of all possible round trips and then selecting one with the smallest distance. However, this is no longer practicable for a small number of cities. In the simplest variant, the symmetrical TSP with cities, there are various round trips, that is over 43 billion in 15 cities and over 177 trillion in 18 cities . The following example shows how quickly the computing time grows with a growing number of cities: If you have a computer that calculates the solution for 30 cities in one hour, it needs almost a thousand times the time for two additional cities; that's more than 40 days.

With methods of integer linear optimization , in particular branch-and-cut , on the other hand, instances in practically relevant orders of magnitude can be proven to be optimally solved or at least the quality of a found tour can be estimated in comparison to an optimal solution. Interpreted geometrically, these methods consider the problem as a convex polytope , i.e. as a multi-dimensional polygon in a -dimensional unit cube , where is the number of edges of the graph. Each corner of this unit cube describes a tour, provided that the associated 0/1 vector satisfies the linear inequalities described above. The hyperplanes belonging to these inequalities therefore cut off corners of the unit cube that do not represent a tour.
The adjacent picture illustrates this for the (very simple) TSP with three nodes. There are also three binary variables and corresponding to the three possible edges between these nodes . There is only one possible tour in this case, namely the one that uses all three edges. This tour satisfies the inequality that states that every tour must have at least two edges. Apart from this tour, which corresponds to point (1,1,1), all points in the red bordered area also satisfy this inequality. The corresponding cutting plane , which is spanned by the red dashed lines, cuts off all corners that correspond to impossible tours with at most one edge, namely the zero vector (0,0,0) and the unit vectors (1,0,0), ( 0,1,0) and (0,0,1). The stronger inequality would cut off everything but the single admissible point (1,1,1) from the unit cube. In this special case, the same effect can already be achieved using the three inequalities of type (1).
By solving many linear programs , cutting off unneeded parts of the unit cube with the help of further cutting planes (for example of type (2) or also comb , clique tree and domino parity inequalities ) and by dividing them into several sub-polytopes with the help of branch-and -Bound an attempt is made to determine a permissible 0/1 corner with a minimum objective function value. A more detailed description of these methods can be found in the article Integer Linear Optimization .
Applying these procedures alone is usually not enough to find good tours quickly. Their main advantage is that they provide information on the minimum length of a shortest tour. With such a lower bound for the optimal solution value, it is possible to estimate how good a found tour is compared to an optimal round trip without knowing it. For example, if you have found a lower bound of 100 and a tour of length 102, an optimal tour can only be between 100 and 102. The so-called optimality gap, i.e. the maximum relative distance between the optimal tour length and the shortest known tour length, is therefore (102-100) / 100 = 2%, i.e. H; the solution value 102 found is at most 2% away from the optimum value. If the length of a found tour is exactly the same as the lower bound, this proves that the found solution is optimal. To find good tours, these exact procedures can be combined with heuristics, some of which are described in the following section.
Heuristics
In order to come to usable solutions quickly, approximation methods motivated by heuristics are usually necessary, which, however, usually do not provide a quality assessment for the solutions found. Depending on whether a heuristic constructs a new tour or whether it tries to improve an existing tour, it is referred to as an opening (also construction ) or improvement process. In addition, there are dual heuristics that calculate minimum lengths for a tour. Metaheuristics can combine several of these individual heuristics in different ways. An overview of most of the heuristics presented here can be found in the Overview section .
Opening procedure

The closest neighbor heuristic corresponds to the intuitive approach of a traveling salesman . Starting from a city, the city chooses the closest one as the following location. This will be continued successively until all cities have been visited and the traveling salesman has returned to the starting point. The related Farthest-Neighbor heuristic visits the most distant city in every step. In every city, the shortest or longest outgoing route must be sought. There can only be as many outgoing edges per city as there are nodes in the graph. This results in an algorithmic complexity of O (n²) , so the number of calculation steps depends on the square of the number of cities. However, the fact that this heuristic does not generally provide the best solution is due to the fact that the distance between the city of origin and the last city visited is not taken into account until the end. The nearest and farthest neighbor heuristics can deliver any number of bad results, that is, there is no constant, instance-independent approximation factor for the solution value compared to the optimal value.
The so-called insertion heuristics form a whole class of further opening procedures . The simplest variants of this are the nearest insertion heuristic (closest insertion) and the farthest insertion heuristic (furthest insertion) . Let there be (a few) neighboring cities for which an optimal round trip can be quickly determined using exact procedures. A step-by-step check is now made to determine which city that has not yet been visited is closest (or farthest) to one of the connecting lines on the previous round trip. Once this city has been found, it will be incorporated into the tour between the cities closest to it. The procedure continues until the tour includes all cities. The solutions to this heuristic can also be as bad as you want in comparison to an optimal solution.

Another class of heuristics divides the set of nodes into individual partitions (for example according to geographical criteria), each of which is partially optimized. The partial solutions are then combined to form an overall solution. As a rule, this is only locally optimal and can be as bad as desired compared to the global optimal.
The minimum spanning tree heuristic (MST) first calculates a minimal spanning tree , i.e. a graph in which all points are connected to one another and which has a minimum length. Starting from this, a tour is constructed by first doubling all the tree edges and then looking for an “ Euler tour” in the resulting Euler's graph . This is abbreviated in the end by direct lines if nodes are visited twice. If the minimum spanning tree is calculated using Kruskal's method, the MST heuristic delivers the same result as the nearest insertion heuristic. Compared to an optimal solution, the result can be as bad as you like. In the case of a metric TSP, however, it can be shown that the tour constructed in this way is at most twice as long as a shortest tour.
An even better approximation quality for metric TSP is achieved by the algorithm by Christofides and Serdyukov . It can be used to calculate a round trip that is at most one and a half times as long as an optimal one. Instead of doubling the edges in the MST heuristic, a smallest perfect pairing is calculated on the nodes of odd degree in the minimally spanning tree in order to generate an Eulerian graph. However, this algorithm is more complex.
Improvement process
Improving optimization processes, also post-optimization processes (post-optimization) try to shorten an existing tour by making small modifications. If none of the changes considered lead to an improvement, then a local optimum has been found (but not necessarily a global one). The k-Opt heuristics follow this approach by systematically removing groups of edges from the tour and replacing them with other edges so that a tour is created again. Since a complete implementation of this procedure would correspond to a list of all possible routes, in practical implementations there is usually a maximum of 5. All exchange possibilities of two and three edges are often tried out, while edge exchanges of more than three edges are only used very sparingly because of the computational effort .
The quality of a k-opt heuristic in practice depends heavily on the selection of the edges to be exchanged and the parameter , for which there are various heuristic criteria. A well-known k-opt-based heuristic is the Lin-Kernighan heuristic , which was developed in 1973 by S. Lin and BW Kernighan and, in the implementation of Keld Helsgaun, was involved, among other things, in the optimal solution of the TSP by 24,978 Swedish locations in 2004 was. It is based on first testing all exchange options for two edges, then those with three edges, etc., until one of several possible termination criteria is met.
Metaheuristic Procedures
Metaheuristics combine local and global search methods in an abstract strategy for the heuristic optimization of a problem. Many of these methods are based on local search ; H. they calculate a heuristic starting solution (for example with the nearest-neighbor heuristic) and improve this using a local search method, such as K-opt heuristics , until no better tour is found. Various strategies such as taboo search or simulated cooling can be used to try to prevent getting stuck in local minima as far as possible. Other approaches, such as ant algorithms , genetic algorithms or artificial neural networks (especially the Hopfield network there ), are based on natural processes. In principle, all of these methods can calculate good solutions, but they can also be as bad as you want in comparison to an optimal solution. Their quality and duration largely depend on the definition and implementation of the individual steps.
Dual heuristics
The traveling salesman problem is one of the few combinatorial optimization problems for which useful lower bounds for the minimum length of a tour (in general: the minimum cost of a solution) can be specified in a simple manner. These limits are particularly important in order to make statements about the quality of a permissible tour. Since, for example, every tour, i.e. in particular also an optimal one, contains precise edges, it must be at least as long as the sum of the smallest edge lengths. Another lower bound results from the observation that when you delete any edge from a tour, a spanning tree arises, i.e. a subgraph that contains all nodes but no circles. The tour is at least as long as this tree and therefore, by definition, at least as long as a minimal spanning tree (i.e. a spanning tree with minimal sum of the edge lengths) that can be easily determined. Since this applies to every tour, the length of a minimal spanning tree provides a lower bound for the length of an optimal tour. In a somewhat more general way, you can also calculate a so-called minimal 1-tree . This is a minimally spanning tree between nodes 2 to (with any numbering), which is connected to the node with the number 1 via the two shortest possible edges (hence the name). Its length also provides a lower bound. Furthermore, every tour is also a perfect 2-matching . This means that a shortest tour must be at least as long as the value of a minimum perfect 2-matching that can be calculated in O (n³).
Overview
The following overview table lists the type of procedure for most of the heuristics presented here, the maximum runtime for cities and any quality guarantees for the calculated solutions. Since the runtime and quality of metaheuristics are heavily dependent on the choice of sub-algorithms and cannot be specified in general, they are not listed here.
| Procedure | Type | running time | Max. Deviation from the optimum |
|---|---|---|---|
| Nearest Neighbor Heuristic | Opening heuristic | Factor (log (n) +1) / 2 (metric TSP) | |
| Farthest Neighbor Heuristic | Opening heuristic | any size | |
| Farthest insertion heuristic | Insertion heuristic | any size | |
| Nearest insertion heuristic | Insertion heuristic | any size, factor 2 (metric TSP) | |
| Minimum spanning tree heuristic | Opening heuristic | like nearest-insertion | |
| Christofides heuristic | Opening heuristic | Factor 1.5 (metric TSP) | |
| K-opt heuristic | Improvement heuristic | per step | any size |
| Sum of the n shortest edges | Dual heuristics | any size | |
| Length of a minimal spanning tree | Dual heuristics | any size |
Practical Limits to Predictability
The largest non-trivial instance of a (symmetrical) round trip problem that has been solved optimally so far is a planning problem for the layout of integrated circuits with 33,810 nodes. This record was set in 2005 by William Cook and others with the help of a combination of various heuristics and the branch-and-cut- based program Concorde , using earlier partial results from various university working groups as a basis. The largest optimally resolved instance up to then consisted of 24,978 Swedish cities, resolved in 2004. With the help of special decomposition techniques and the use of several parallel computers, William Cook found tours for a TSP to over 526 million stars , the length of which has been proven to be at most 0.798% deviates from the optimum.
However, the fact that a TSP of a certain size could be optimally solved does not mean that every instance of this size can be optimally solved, since - as with most combinatorial optimization problems - the difficulty of the solution depends heavily on the input parameters (in this case the edge weights). A smaller problem can be much more difficult to solve; For example, in the TSPLIB there is an instance with only 225 cities that is difficult to solve because of its many symmetries. In the case of TSPs that arise from practical applications, other secondary conditions, such as time windows, often have to be taken into account. Therefore, the largest optimally solvable problem instances of such variants are usually much smaller than in the classic traveling salesman problem, so that in practice heuristic approaches are often used to solve the problem. Combinations of heuristic procedures with LP -based procedures such as branch-and-cut are mainly used in research in order to be able to assess the quality of solutions and solution procedures with the help of lower bounds for the tour length.
Variants and applications
Even the classic variant of the problem occurs in many applications, for example in DNA sequencing , in the layout of integrated circuits or in the control of a drill in the manufacture of printed circuit boards . Astronomers are also looking for the shortest route from star to star when surveying the sky.
The multitude of combinable variants together form the TSP family - all of which are considered NP-difficult . Some of the generalizations consider several traveling salesmen, while other variants differ from the classic version through fundamentally changed optimization criteria or additional constraints.
The procedure in practice differs from mathematical theory in that one is usually not looking for the best solution, but only a sufficiently good one. The total effort must be considered here - as effort for implementation and calculation. What “good” means and which criteria are used depends on the context of the problem. This means that you will make less effort for a one-off delivery tour than for the assembly planning of a circuit board that is produced in millions.
Several traveling salesmen
With the multiple TSP (mTSP) , the cities are divided among several commercial travelers, with all of their round trips starting and ending in the same city. Each city must be visited by exactly one traveling salesman. The aim is to minimize the total distance covered. In the mTSP with nonlazy salesmen variant , only round trips with at least two cities are permitted, so that every round traveler actually has to get around. The classic version is a special case with only one traveling salesman.
The Vehicle Routing Problem (VRP) is a multiple TSP with additional transport capacity restrictions. It arose directly from the practical necessity of route planning , in which goods are to be delivered to customers from a central depot. The round trips correspond to the tours of vans that start from the shared depot and return there. The aim of the VRP is to supply all customers as cheaply as possible. A customer can be supplied multiple times, but only from one van at a time. In the special case that the capacities of the vans are greater than the sum of all order quantities, the VRP corresponds to the mTSP and is therefore also NP-heavy . Variants derived from the Vehicle Routing Problem ( VRP ) are:
- Capacitated VRP ( CVRP )
- All vans have a maximum capacity.
- Multiple Depot VRP ( MDVRP )
- The transporters can start from several different depots.
- VRP with Time Windows ( VRPTW )
- The customers can only be supplied within a given time frame.
- Periodic VRP ( PVRP )
- The needs of the customers grow at intervals. A certain period of time is considered.
- Split Delivery VRP ( SDVRP )
- A customer can be supplied by different transporters.
- VRP with Backhauls ( VRPB )
- Suppliers and their delivery quantities are taken into account.
- Dynamic VRP ( DVRP )
- Additional requirements can arise during the calculation, which must be taken into account in advance.
City clusters
With the generalized TSP (GTSP) (German: generalized TSP) several cities are combined into a cluster. The traveling salesman has to visit exactly one city from each cluster. The TSP is a special case of the GTSP, in which each city is in a cluster that only contains this one city. Each instance of the GTSP can be converted into an instance of the simple TSP and solved with the algorithms known for this problem. For this reason, the GTSP is also NP-difficult.
In practice, the solution algorithms of the GTSP are used, for example, to optimize the idle travel of CNC cutting machines . These are used, among other things, in the textile industry to cut out small pieces of clothing from a large sheet of fabric. The contours to be cut represent the clusters and the possible starting points of the cutting tool on the contours represent the cities.
Changes to the optimization criterion
With Prize Collecting TSP ( PCTSP ), the traveling salesman is paid certain prize money in each city (for example sales revenues ). In order to travel from one city to the next, however, he has to raise costs. He should now select a specified number of cities and a round trip between these cities so that the profit is maximum. Since the problem contains the classic variant as a special case (all cities are visited and all prize money is 0), the PCTSP is also NP-difficult. A form derived from this is the Traveling Salesman Selection Problem ( TSSP ), in which a specified shortest route between any cities is sought, with no prize money and metric distances being assumed.
With the Bottleneck TSP ( BTSP ) it is not the sum of the edge lengths that should be minimized, but the length of the longest edge used. This causes the individual distances to vary less widely in order to counteract possible bottlenecks, the bottlenecks . A related variant is the maximum scatter TSP , in which the smallest length used is maximized.
Additional constraints
A common limitation in applications are time slots during which a city must be visited. For example, a technical customer service for the repair of household appliances usually agrees with customers on a period of time during which the technician will visit. This period must be taken into account when planning the tour.
With the online TSP , not all cities are given in advance, but only become known gradually while the traveling salesman is already on the way. He then changes his tour so that new cities fit "as well as possible" into his previously planned tour. This variant occurs, for example, with breakdown services such as the ADAC , where the positions of broken down cars are only gradually known and the headquarters tries to incorporate new cases into existing tours as cheaply as possible. Since there are many breakdown helpers on the road and when a breakdown is reported, the central office gives an approximate time of when a breakdown helper will arrive, it is a multiple online TSP with time windows .
The parcel service UPS with around 55,000 courier drivers and an average of 120 parcels per day and driver used previously optimized static routes for each vehicle, which were individually modified by the drivers according to their experience. From 2013 the company will switch to the ORION ( On-Road Integrated Optimization and Navigation ) system . This takes into account guaranteed delivery times for individual parcels, registered collections and special customer classes with preferred service as well as data from the traffic flow in real time. It leaves experienced staff the option to deviate from the suggested route. For this company, there is an additional condition that UPS drivers do not turn left in cities with a regular road grid because this entails excessive delays in waiting for oncoming traffic and an excessive risk of accidents.
Individual evidence
- ^ René van Bevern, Viktoriia A. Slugina: A historical note on the 3/2 approximation algorithm for the metric traveling salesman problem . In: Historia Mathematica . May 2020, doi : 10.1016 / j.hm.2020.04.003 , arxiv : 2004.02437 ( elsevier.com ).
- ^ David L. Applegate, Robert E. Bixby, Vašek Chvátal, and William J. Cook: The Traveling Salesman Problem. A Computational Study . Princeton University Press, February 2007. pp. 522-524. ISBN 0-691-12993-2
- ↑ András Sebö, Jens Vygen: Shorter tours by nicer ears: 7/5 approximation for the graph-TSP, 3/2 for the path version, and 4/3 for two-edge-connected subgraphs . Combinatorica 34 (5) (2014), 597-629, ( doi: 10.1007 / s00493-011-2960-3 )
- ↑ Pjotr Berman, Marek Karpinski, 8/7-approximation algorithm for (1,2) -TSP , Proceedings SODA '06, pp. 641-648. doi: 10.1145 / 1109557.1109627
- ↑ Marek Karpinski, Michael Lampis, and Richard Schmied, New Inapproximability Bounds for TSP , appeared in Algorithms and Computation - 24th International Symposium, ISAAC 2013, pp. 568-578, 2013, doi: 10.1007 / 978-3-642-45030-3
- ^ Marek Karpinski, Richard Schmied: Approximation Hardness of Graphic TSP on Cubic Graphs . In: RAIRO Operations Research . No. 49, 2015, pp. 651-668.
- ^ Sanjeev Arora: Polynomial Time Approximation Schemes for Euclidean Traveling Salesman and other Geometric Problems . In: J. ACM . 45, No. 5, 1998, pp. 753-782. doi : 10.1145 / 290179.290180 .
- ^ Joseph SB Mitchell: Guillotine Subdivisions Approximate Polygonal Subdivisions: A Simple Polynomial-Time Approximation Scheme for Geometric TSP, k-MST, and Related Problems . In: SIAM J. Comput. . 28, No. 4, 1999, pp. 1298-1309. doi : 10.1137 / S0097539796309764 .
- ^ A b William Cook, Daniel Espinoza, Marcos Goycoolea: Computing with Domino-Parity Inequalities for the TSP. 2005. (Preprint, pdf; 261 kB)
- ↑ Keld Helsgaun: An Effective implementation of the Lin-Kernighan Traveling Salesman Heuristic. (PDF; 646 kB) In: European Journal of Operational Research. Amsterdam 126.2000, No. 1, pp. 106-130. ISSN 0377-2217
- ↑ After Rosenkrantz, DJ; Stearns, RE; Lewis, PM "Approximate algorithms for the traveling salesperson problem," Conference on Switching and Automata Theory, 1974. doi: 10.1109 / SWAT.1974.4
- ^ TSP page by Vašek Chvátal
- ^ Documented applications of Concorde
- ↑ Wired.com: The Astronomical Math Behind UPS 'New Tool to Deliver Packages Faster , June 13, 2013
- ^ New York Times: Left-Hand-Turn Elimination , December 9, 2007
literature
- David Applegate, Robert Bixby , Vašek Chvátal , William Cook : On the Solution of Traveling Salesman Problems . Documenta Mathematica. Extra volume 3 for the International Congress of Mathematicians. Berlin 1998, pp. 645-656. ( Postscript ; Gzip ; 68 kB)
- David L. Applegate, Robert E. Bixby, Vašek Chvátal, and William J. Cook: The Traveling Salesman Problem. A Computational Study . Princeton University Press, February 2007. ISBN 0-691-12993-2
- William J. Cook: In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation. Princeton University Press 2011, ISBN 0-691-15270-5 .
- Lawler, Lenstra, Rinnooy Kan, Shmoys (Eds.): The Traveling Salesman Problem. A Guided Tour of Combinatorial Optimization . Wiley, Chichester 1985. ISBN 0-471-90413-9
- W. Domschke: Logistics - round trips and tours . Oldenbourg-Verlag, Munich / Vienna 1997 (4th edition). ISBN 3-486-29472-5
- T. Grünert, S. Irnich: Optimization in transport. Vol. 2. Paths and tours. Shaker Verlag , Aachen 2005. ISBN 3-8322-4515-4
- Gregory Gutin, Abraham P. Punnen: The traveling salesman problem and its variations . Kluwer Academic Publishers. Excerpts online (English)
- Walter Schmitting: The Traveling Salesman Problem - Applications and Heuristic Use of Voronoi- / Delaunay Structures for Solving Euclidean, Two-Dimensional Traveling Salesman Problems .
Web links
- TSP game - an interactive game for the traveling salesman problem with detailed explanation and illustration of the solution process
- The Traveling Salesman Problem Home - detailed information about the Traveling Salesman Problem (English)
- TSPLIB - Collection of benchmark instances of the TSP and various variants (English)
- Spectrum of Science (4/99): The optimized Odyssey - Article by Martin Grötschel and Manfred Padberg
- The VRP Web - detailed information about the vehicle routing problem (English)
- 40th algorithm of the week - IT year 2006 TSP or the optimal tour for St. Nicholas
- Free Tourplan - Open source software for solving tour planning problems, including TSP















































![[0.1] ^ m](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7ad28c4c962381ae011e67434abe5e9a8504f7)






