Cutting plane method

A cutting-plane method (engl. Cutting plane algorithm ) is applied mathematics an algorithm for solving integer linear programming problems . The basic idea is to consider its LP relaxation (i.e. without integer conditions) instead of an integer linear program and to tighten it step by step by adding further inequalities until (ideally) an integer solution is found.

That in the 1950s u. a. The method developed by Delbert Ray Fulkerson , George Dantzig and later by Egon Balas and Ralph Gomory , with its further developments, is today one of the standard methods in integer optimization and continues to be the subject of current research. It is usually not sufficient as the sole solution method, but it delivers good dual bounds for the optimization problems to be solved. It is therefore often combined with branch-and-bound to create the so-called branch-and-cut method .

Problem definition

A cutting-plane method is used to solve integer programs ( Engl. Integer program , IP) in the normal form

${\displaystyle \max\{c^{T}x\;|\;Ax\leq b,x\geq 0,x\in \mathbb {Z} ^{n}\}.}$

Here is a real matrix and and are vectors of suitable dimensions. The condition is to be understood component-wise, i.e. as ${\displaystyle A}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle Ax\leq b}$

${\displaystyle a_{i}\cdot x=\sum _{j=1}^{n}a_{ij}x_{j}\leq b_{i}}$

for all rows of the matrix . The condition also means that all entries in the vector must be non-negative. ${\displaystyle i}$ ${\displaystyle A}$ ${\displaystyle x\geq 0}$ ${\displaystyle x}$

Polytope of permissible integer points (red) with LP relaxation (blue)

This can be interpreted geometrically as follows: the amount

${\displaystyle P:=\{x\;|\;Ax\leq b,x\geq 0\},}$

which arises from the omission of the integer conditions, forms a convex polyhedron in -dimensional space, whose limiting hyperplanes correspond to the lines of the inequality system. contains u. a. all admissible points of the initial system, i.e. all integer points that meet the conditions , but in contrast to linear optimization, not all points in are admissible. The linear program ${\displaystyle n}$ ${\displaystyle P}$ ${\displaystyle Ax\leq b}$ ${\displaystyle P}$

${\displaystyle \max \,\{c^{T}x\;|\;x\in P\}}$

is called LP relaxation of the integer problem.

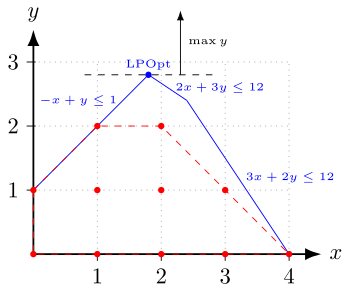
In the picture opposite is the integer linear program (IP)

${\displaystyle {\begin{matrix}\max &&y\\&-x&+y&\leq 1\\&3x&+2y&\leq 12\\&2x&+3y&\leq 12\\&x,y\in \mathbb {Z} _{+}\end{matrix}}}$

shown. The admissible integer points are drawn in red, and the red dashed lines mark their convex hull , i.e. the smallest polyhedron that contains all these points. This polyhedron should actually be optimized, but it is usually not exactly known. The blue lines together with the coordinate axes delimit the polyhedron of the LP relaxation, which is given by the inequality system without integer conditions. The aim of the optimization is to move the black dashed line parallel upwards (in the direction of the vector ) so far that it just touches the respective polyhedron. The optimal solutions of the integer problem are therefore the points and with the objective function value . The - in this case unambiguous - optimal solution of the LP relaxation with the objective function value 2.8 is the point marked in blue , which is not an integer and is therefore not permissible for the IP. ${\displaystyle P}$ ${\displaystyle c=(0;1)}$ ${\displaystyle (1;2)}$ ${\displaystyle (2;2)}$ ${\displaystyle c^{T}x=(0;1)^{T}(1;2)=2}$ ${\displaystyle LP_{opt}=(1,8;2,8)}$

Basic idea of ​​the algorithm using the example

Adding a cutting plane (green)

Cutting plane methods first calculate a solution for the LP relaxation. This is usually not an integer (like the point ), but provides an upper (generally: dual ) bound for the optimal value of the IP, since every solution of the integer program is also a solution of the LP relaxation and therefore the optimal value of the integer program (in Example 2) can be at most as high as the optimal value of the LP relaxation (in the example 2.8). This can be used to estimate the quality of a solution of the IP. ${\displaystyle LP_{opt}=(1{,}8;2{,}8)}$

This dual barrier is then tightened by gradually adding so-called cutting planes . A cutting plane is an additional inequality that is satisfied by all feasible points of the IP, but not by the current LP solution. If the inequality is added to the LP, another solution must come out when the solution is again. This is continued until an integer solution is found (which is then automatically also optimal for the integer program) or no more suitable inequalities are found.

The image on the right shows the cutting plane (green) that separates ( separates ) the previous LP optimum (blue) from the IP polyhedron . All permissible points lie on one side of the hyperplane, the LP solution on the other side. Solving the LP again with this additional inequality yields the point marked in green (4/3; 7/3). This point is still not permissible, but it has the smaller objective function value, which improves the upper bound to this value. ${\displaystyle x+2y\leq 6}$ ${\displaystyle 7/3\approx 2{,}333}$

The best cutting planes that can be found are facets of the IP polyhedron, i.e. -dimensional side surfaces for variables. In the example above, these are the inequalities and , which correspond to the red dashed lines. ${\displaystyle (n-1)}$ ${\displaystyle n}$ ${\displaystyle y\leq 2}$ ${\displaystyle x+y\leq 4}$

Use in practice

For a whole range of planning problems, especially those with a practical application background (e.g. routing problems or assignment problems), several classes of inequalities are known that are fulfilled by all integer points of the polyhedron (i.e. are valid for this polyhedron ). These can be problem-independent IP cutting planes such as Gomory cuts , which can be found by standard solvers even without knowledge of the practical background, or problem-specific cutting planes that take advantage of the special structure of the matrix . Examples of the latter are the short cycle inequalities in the traveling salesman problem . Since there is an exponential number of short cycle inequalities in relation to the number of nodes in the graph, they can initially be omitted and instead separated gradually . ${\displaystyle A}$

Finding such classes of valid inequalities for certain types or substructures of integer programs and making statements about the quality of these cutting planes is a non-trivial problem. In particular, the information about the conditions under which a section plane defines a facet of the underlying polyhedron generally requires a more precise mathematical investigation. This is an important subject of current research in integer linear optimization .

If some classes of valid inequalities are known, the following algorithm is usually used:

1. Solve the LP relaxation; be the optimal solution of the LP. ${\displaystyle x^{*}}$
2. If is an integer, it is also optimal. STOP. ${\displaystyle x^{*}}$
3. Test for all known classes of inequalities whether they contain one or more of the violated cutting planes. ${\displaystyle x^{*}}$
4. If so, add it to the LP and go to 1. Otherwise STOP.

If at the end no more violated cutting plane is found without the LP solution being an integer, one can try to heuristically determine an integer solution or start branch-and-bound (this combination is then called branch-and-cut ). In practice, this works sometimes more and sometimes less well, depending on the problem and the model used.

How to test the inequalities for violation in step (3) depends on the inequalities. In some cases the cutting planes can be separated exactly , i. H. if you don't find a violated inequality of this class, there isn't any. This is the case, for example, when a class contains so few inequalities that you can simply test them all through. But also the exponential number of short cycle inequalities in the case of the TSP can be tested for violation by calculating a minimum cut in the underlying graph in polynomial time. In other cases, where the separation is only possible heuristically within a reasonable time (for example with general mixed-integer rounding cuts ), in the end it is not clear whether there are no more violated inequalities or whether they have just not been found.

history

The first cutting planes were developed in the mid-1950s by DR Fulkerson , G. Dantzig, and S. Johnson for the traveling salesman problem . Without knowledge of this work and motivated by former colleagues in the US Navy who were interested in integer solutions, R. Gomory developed the first generally applicable cutting plane method in 1958 during his stay in Princeton . He showed that theoretically any whole number programs can be solved with this method alone. In practice, however, this approach has two problems: on the one hand, many cutting planes lead at some point to very large linear programs and correspondingly long solution times in each iteration, and on the other hand, the cutting inequalities proposed by Gomory ( Gomory fractional cuts ) often contain very many non-zero coefficients, which leads to numerical instabilities in solving the linear programs. Nevertheless, this procedure represented a decisive algorithmic advance.

In the 1980s , M. Padberg and others worked on cutting planes for sub-structures that often crop up, such as backpack problems , which can often be used in a more general context. In the last ten years many cutting planes have been discovered for special application problems, such as routing problems that arise in connection with the planning of public transport networks or the design of telecommunications networks .

literature

• George Nemhauser and Laurence Wolsey: Integer and Combinatorial Optimization. Wiley Interscience, 1988, ISBN 0-471-35943-2 .
• Ralph Gomory: Early Integer Programming. In: Operations Research, Volume 50, Number 1, pp. 78-81, 2002.

Web links

• Description of cutting planes for the traveling salesman problem