Branch-and-cut

In combinatorial optimization , a sub-area of discrete mathematics , branch-and-cut, or branching and cut, describes a method for solving integer linear optimization problems . The method consists of a combination of the cutting plane method and branch-and-bound .

history

While cutting planes and branch-and-bound were already developed in the 1950s and 1960s , it was not until the 1980s that these processes were combined to create branch-and-cut. One of the first applications of this method was the investigation of the traveling salesman problem by Manfred Padberg , Martin Grötschel and others, which contributed significantly to the further development of Branch-and-Cut. In the 1990s , George Nemhauser , Laurence Wolsey , Robert Bixby and others developed new cutting planes for various combinatorial optimization problems, better branching rules and clever combinations of both methods, which has made branch-and-cut a standard tool for integer linear optimization today. The best solvers for integer linear programs today are based on this principle, and the methods of solving them are still evolving.

Basic idea

The goal of integer linear optimization is to maximize (or minimize) a linear objective function over a polyhedron , which is given by a linear system of inequalities, whereby only integer points are allowed:

{\ displaystyle \ max \ {c ^ {T} x \; | \; Ax \ leq b, x \ geq 0, x \ in \ mathbb {Z} ^ {n} \}}

In general terms, this problem is NP-complete ; H. it probably cannot be solved efficiently. A standard approach of the integral linear optimization is the solution of the so-called LP relaxation of this system, i.e. the linear program that is created by omitting the integer conditions. This problem can be solved comparatively easily, for example with the simplex method .

Cutting plane method

Adding a cutting plane (green)

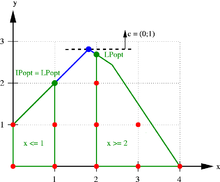
The LP relaxation solution fulfills the conditions , but is usually not an integer. A cutting plane method now adds further inequalities to the system, which are satisfied by all admissible (integer) points, but not by the current solution of the LP relaxation. When solving the system again with the new inequalities, another solution must come out, which is hopefully “closer” to the desired optimum. If the new solution is an integer, it is also optimal for the original problem. Otherwise you have to look for new cutting planes again. Geometrically, adding a further inequality corresponds to the determination of a hyperplane (green in the picture) that separates the LP solution (blue point at the top) from the mostly unknown polyhedron of the integer points (red). ${\ displaystyle Ax \ leq b}$

Branch-and-Bound

Breakdown of the problem into the sub-problems with and

{\ displaystyle x \ leq 1}

{\ displaystyle x \ geq 2}

If no further cutting planes are found that could still be added without the current solution being an integer, a branch-and-bound process is started. This divides the problem into two sub-problems. A standard practice is branching on a single variable. For example, if a variable that should actually be an integer has the value 1.8 in the current LP solution, this variable is restricted to in one sub-problem and to in the other (see figure). As a result, the set of feasible solutions is divided into two disjoint , i.e. non-overlapping parts, since each feasible solution must meet exactly one of the two conditions. Instead of setting limits on individual variables, further linear inequalities can also be added to each sub-problem. ${\ displaystyle x}$ ${\ displaystyle x \ leq 1}$ ${\ displaystyle x \ geq 2}$

Through iterative application of this method, a decision tree is built in which a sub-problem is restricted the more deeply it lies in the tree. In this way, the entire solution space can be searched systematically. An advantage of this method compared to the pure enumeration of all solutions is the fact that in some cases complete subtrees can be cut off ( bounding ), because it is clear that this subtree cannot contain an optimal solution.

Combination to branch-and-cut

Because section planes for LP relaxation were already added before the branch-and-bound process, the method often finds a solution much faster than if the branch-and-bound tree is built on the original LP relaxation. In addition, additional cutting planes can often be determined during branching that would not have been found without the restrictions in the sub-problems. These cutting planes can either be globally valid , i.e. permitted for the original problem, or locally valid , i.e. only permitted for the current subtree with its restrictions. Furthermore, additional heuristics for the determination of permissible solutions can be called up in the individual sub-problems , whereby further sub-trees can be cut off early.

Evaluation of the procedure

Branch-and-cut has proven to be clearly advantageous compared to pure branch-and-bound or cutting plane methods . A main advantage of the method compared to heuristics in practice is that it is generic, i.e. it can be used as a standard solution method for a whole series of optimization problems, while heuristics usually have to be developed problem-specifically. As a further advantage over the sole application of most heuristics, the branch-and-cut method provides an estimate of how good a solution found is compared to an optimal solution without knowing it itself. However, the solution times until an optimal solution is found including the proof of optimality can be very long. In fact, with many integer linear programs, good solutions are found in a short time, but the proof of optimality takes a very long time. A variant that is widespread at least in research is therefore to quickly calculate good solutions in the individual sub-problems with generic or problem-specific heuristics, the quality of which can then be estimated using the entire branch-and-cut method. When a solution is reached that is, for example, at most 5% worse than an optimal solution, the process can be terminated if this solution quality is sufficient for practical purposes.

literature

George Nemhauser and Laurence Wolsey: Integer and Combinatorial Optimization. Wiley Interscience, 1988, ISBN 0-471-35943-2 .