polyhedron
A (three-dimensional) polyhedron [ poliˈ (ʔ) eːdɐ ] (also polyhedron , polyhedron or planar ; from ancient Greek πολύεδρος polýedros , German 'many seated, polygonal' ) is in the narrower sense a subset of three-dimensional space , which consists exclusively of straight surfaces (planes) is limited, for example a cube or an octant of a three-dimensional coordinate system.
Examples of polyhedra
Examples of polyhedra from everyday life - understood as geometric bodies - are (in their usual construction) cupboards, pyramids , houses, crystals , dice or geodesic domes . Balls , cones , bottles, pieces of cake, however , are not polyhedra because they have curved edges. The most important polyhedra are cubes , cuboids , prisms , pyramids and spades (parallelepipeds).
Special three-dimensional polyhedra
Polyhedra, as we encounter them in everyday life or as we know them from school mathematics (see previous section), are three-dimensional and limited, i.e. - in the sense of topology - compact subsets of three-dimensional Euclidean space. They are therefore one of the geometric bodies . A polyhedron is called three-dimensional if it is not completely contained in any plane. A polyhedron is called constrained if there is a sphere in which the polyhedron is completely contained. Unconstrained polyhedra with only one corner are called polyhedron cones. These include the Trieder ( English trihedron ).
Convex polyhedron
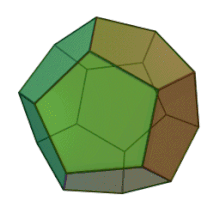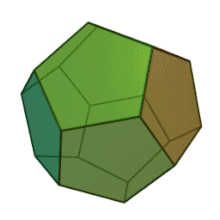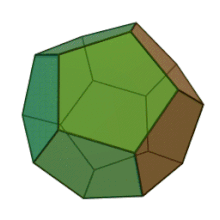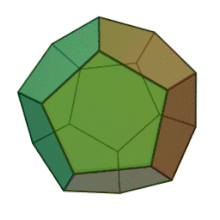
Often three-dimensional polyhedra are also convex . A polyhedron is called convex if for every two points of the polyhedron the connecting line between these points lies completely in the polyhedron. For example, the adjacent dodecahedron is convex. An example of a non-convex polyhedron is the toroidal polyhedron shown below.
Regular polyhedra
Different types of regularities can occur in polyhedra. The most important are:
- The side faces are regular polygons .
- All side faces are congruent .
- All corners are the same, that is, for every two corners the polyhedron can be rotated or mirrored so that it is converted into and the new polyhedron is congruent with the original.
Polyhedra that meet all 3 conditions are called regular polyhedra .
Platonic, Archimedean, Catalan, and Johnson solids
There are exactly 5 convex polyhedra that are regular polyhedra (that is, meet all three conditions), the Platonic solids .
The convex polyhedra that only fulfill the first and third condition are (certain) prisms , antiprisms and the 13 Archimedean solids .
The convex polyhedra that only satisfy the second condition are the 13 Catalan solids . More precisely, the somewhat stronger condition of the similarity of the sides (analogous to 3.) must be fulfilled for this.
The convex polyhedra that only satisfy the first condition are the 92 Johnson solids .
Orthogonal polyhedra
The faces of an orthogonal polyhedron meet at right angles . Its edges run parallel to the axes of a Cartesian coordinate system . With the exception of the cuboid , orthogonal polyhedra are not convex. They expand the two-dimensional orthogonal polygons into the third dimension. Orthogonal polyhedra are used in algorithmic geometry . There their restricted structure offers advantages in dealing with otherwise unsolved problems (any polyhedron). One example is unfolding the polyhedron surfaces into a polygonal mesh.
Chiral polyhedra
Chiral polyhedra are polyhedra that do not match their mirror image. Examples in three dimensions are the beveled cube and the crooked decahedron . They show handedness , that is, they have a right-handed and a left-handed variant, which can be mapped to one another by mirroring.
Euler's polyhedron substitute and Euler characteristic
For convex and bounded polyhedra, Euler's polyhedron equation applies:
Here is the number of corners, the number of faces and the number of edges.
The condition “convex” is essential. Example: The points of three-dimensional space with the (right-angled Cartesian) coordinates (x, y, z), where the absolute value of x, y and z is less than or equal to 2, form a cube with edge length 4. If we derive the If you remove points whose coordinates are all less than 1, you get a non-convex polyhedron, namely a cube with a smaller cube drilled inside, with 16 corners, 24 edges and 12 faces, in which Euler's polyhedron theorem does not apply.
For connected polyhedra (to which the above example does not belong) applies in general
with the Euler characteristic . For a torus, for example, is . The polyhedron shown on the right is an example of this. There has corners 24, 72 edges and 48 surfaces: .
designation
Polyhedra are generally classified according to the number of bounding faces.
| Area number | Surname | example | image |
|---|---|---|---|
| 4th | Tetrahedron | = Triangular pyramid |

|
| 5 | Pentahedron | Square pyramid |

|
| 6th | Hexahedron | cube |
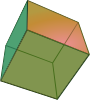
|
| 7th | Heptahedron | elongated triangular pyramid |

|
| 8th | octahedron | Truncated rhombohedron |

|
| 9 | Enneaeder | elongated square pyramid |
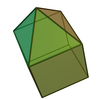
|
| 10 | Decahedron | Pentagonal bipyramid |

|
| 11 | Hendekaeder |

|
|
| 12 | Dodecahedron | regular dodecahedron |

|
| 13 | Tridecahedron | twisted elongated square pyramid |
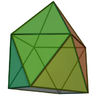
|
| 14th | Tetradecahedron | Disheptahedron |

|
| 15th | Pentadecahedron | elongated pentagonal bipyramid |
|
| 16 | Hexadecahedron | twice expanded antiprism |

|
| 17th | Heptadecahedron | enlarged sphenocorona |

|
| 18th | Octadecahedron | Square double dome |

|
| 19th | Enneadekaeder | ||
| 20th | Icosahedron | regular icosahedron |

|
| 22nd | Ikosidiploeder | elongated pentagonal dome |

|
| 24 | Icositetrahedron | Deltoidal icositetrahedron |

|
| 30th | Triacontahedron | double expanded truncated hexahedron |

|
| 32 | Triacontadiploeder | Truncated icosahedron |

|
| 60 | Hexacontahedron | double expanded truncated hexahedron |

|
| Pentagon hexacontahedron |

|
duality
For every convex polyhedron there is a dual polyhedron. Each corner of the polyhedron is bijectively assigned an area of the dual polyhedron and vice versa. In addition, an edge of the dual polyhedron is bijectively assigned to each edge .
The dual of a convex polyhedron can be obtained by polar reciprocating motion. Dual polyhedra exist in pairs, and the dual of a dual is again the original polyhedron. Some polyhedra are self-dual, which means that the polyhedron's dual is congruent with the original polyhedron. Such polyhedra are for example the tetrahedron , the square pyramid and all regular pyramids .
The dual of a platonic solid is itself a platonic solid. The hexahedron is dual to the octahedron and vice versa, the dodecahedron is dual to the icosahedron and vice versa and the tetrahedron is dual to itself. Each of the 13 Archimedean solids is dual to one of the 13 Catalan solids and vice versa.
Abstract polyhedra also have duals, which additionally ensure that they have the same Euler characteristics and orientability as the original polyhedron. However, this form of duality does not describe the shape of a dual polyhedron, only its combinatorial structure. For some definitions of non-convex geometric polyhedra there exist polyhedra whose abstract duals cannot be realized as geometric polyhedra under the same definition.
Generalizations
In addition to the term polytope , the term “polyhedron” is often used for spaces that are not necessarily three-dimensional.
- Especially in topology , a subset of a polyhedron is called a polyhedron if it can be triangulated, i.e. if it can be formed as a union of the simplexes of a simplicial complex . The homeomorphic picture of such a general polyhedron is called a curved polyhedron and the pictures of the simplexes involved are called crooked simplexes .
- In linear optimization , a (convex) polyhedron is defined as the intersection of finitely many half-spaces . According to this definition, a polyhedron is not necessarily restricted. A bounded, non-empty polyhedron is then called a polytope. According to the decomposition theorem for convex polyhedra , a subset of is a polyhedron if and only if it can be represented as the sum of a convex polytope and a (convex) polyhedral cone.
Web links
- Polyhedron garden images, animations, VRML 3D models; with aesthetic standards
- Formulas for regular and semi-regular polyhedra
- Paper Models of Polyhedra Stencils for making polyhedra
- Polyhedron from braided strips Create polyhedron models by braiding paper strips without using glue
Individual evidence
- ^ Wilhelm Pape , Max Sengebusch (arrangement): Concise dictionary of the Greek language . 3rd edition, 6th impression. Vieweg & Sohn, Braunschweig 1914 ( zeno.org [accessed on March 12, 2020]).
- ^ Edward S. Popko: Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere . CRC Press, 2012, ISBN 978-1-4665-0429-5 ( limited preview in Google Book Search).
- ^ H. Martyn Cundy, AP Rollett: Mathematical models . In: Clarendon Press . , Oxford 1961, pp. 78-79.
- ↑ B. Grünbaum, GC Shephard: Convex polytopes . In: Bulletin of the London Mathematical Society . 1, No. 3, 1969, pp. 257-300. doi : 10.1112 / blms / 1.3.257 .
- ↑ Egbert Harzheim : Introduction to Combinatorial Topology (= DIE MATHEMATIK. Introductions to the subject matter and results of its sub-areas and related sciences ). Scientific Book Society , Darmstadt 1978, ISBN 3-534-07016-X , p. 34 ( MR0533264 ).
- ^ John M. Lee : Introduction to Topological Manifolds (Graduate Texts in Mathematics 202) . Springer, New York [et al.] 2000, ISBN 0-387-98759-2 , pp. 149 .
- ↑ Egbert Harzheim : Introduction to Combinatorial Topology (= DIE MATHEMATIK. Introductions to the subject matter and results of its sub-areas and related sciences ). Scientific Book Society , Darmstadt 1978, ISBN 3-534-07016-X , p. 35 ( MR0533264 ).
- ^ Rainer E. Burkhard, Uwe T. Zimmermann: Introduction to Mathematical Optimization (= Springer textbook ). Springer, Berlin / Heidelberg 2013, ISBN 978-3-642-28673-5 , pp. 19 .















