Bullet
In geometry, a sphere is the abbreviation for spherical surface or spherical body.
Spherical surface and spherical body
The spherical surface is by the rotation of a circle formed around a circle diameter surface . It is a surface of revolution and a special second-order surface and is described as the set (the geometric location) of all points in three-dimensional Euclidean space whose distance from a fixed point in space is equal to a given positive real number . The fixed point is called the center or center of the sphere, and the number is called the radius of the sphere.
The spherical surface divides the space into two separate open subsets , of which exactly one is convex . This amount is called the interior of the sphere. The union of a spherical surface and its interior is called a spherical body or solid sphere . The spherical surface is also called the spherical surface or sphere .
Both spherical surfaces and spherical bodies are often referred to as spheres for short, whereby it must be clear from the context which of the two meanings is meant.
A spherical surface with center ( , , ), and the radius is the set of all points ( , , ) for which
is satisfied.
In vector notation with , :
- ,
- ,
- or
- .
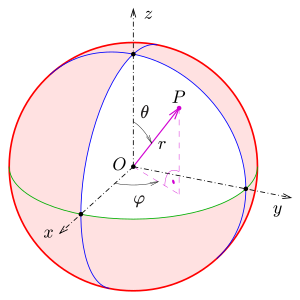
The points on the spherical surface with the radius and the center at the origin can be parameterized using spherical coordinates as follows:
with and .
Spherical cuts
- Putting a plane with a bullet to cut , always results in a circle. If the plane contains the center of the sphere, the line of intersection is called the great circle , otherwise the small circle .
- Both this part of the body resulting hot spherical segment or ball segment , in the case of the great circle hemisphere (hemisphere) .
- The curved part of the surface of a spherical segment is called a spherical cap , spherical cap or spherical cap .
- A spherical segment and the cone with the circle of intersection as the base and the center of the sphere as the tip result in a spherical segment or spherical sector .
- Two parallel planes that intersect the sphere (not touching ) cut a spherical layer out of the sphere . The curved part of the surface of a spherical layer is called the spherical zone .
- Two intersecting planes, whose line of intersection lies partially within the sphere, cut an object from the sphere, the curved surface of which is the spherical triangle .
- A spherical shell ( hollow sphere ) is the difference between two concentric spheres with different radii.
Curves on a sphere
Circles
- The intersection of a plane with a sphere is a circle, a point or empty.
If the section is a circle, it can be represented in parameter form : s. Plane section of an ellipsoid .
However, a sphere can also intersect more complicated surfaces in a circle:
- A non-empty section of a sphere with a surface of revolution whose axis goes through the center of the sphere consists of circles and / or points.
In the picture a sphere cuts a cylinder in two circles. If the radius of the cylinder were the same as the radius of the sphere, the section would consist of a contact circle. An ellipsoid of revolution with the same center as the sphere and the radius of the sphere as the major semi-axis would touch the sphere at two points (vertices).
This property is used in descriptive geometry for the construction of points of the intersection curve of surfaces of revolution (see auxiliary sphere method .)
Clelia curves
Is the sphere in parametric form
given, one obtains Clelia curves if one
puts. Special cases of this are: Vivian curves ( ) and spherical spirals ( ).
Loxodrome
The curve on the globe, which always intersects the meridians (longitudinal circles) at the same angle, is a loxodrome . It spirals around the poles, which are its two asymptotic points, i.e. H. it does not contain the poles. It is not a spherical spiral in the above sense. There is no simple relationship between the angles and .
Sections with other quadrics
If a sphere is intersected by another quadric (cylinder, cone ...), intersection curves arise with suitable radii, parameters ...
Example: sphere - cylinder
The intersection curve of the sphere with the equation and the cylinder with the equation consists of the solutions of the non-linear system of equations
(see implicit curve , picture)
Formulas
| Geometric size | formula |
|---|---|
| Sphere radius | |
| Ball diameter | |
| Circumference (great circle) | |
| volume | |
| surface | |
| Projection area / spherical cross-section | |
| Height (spherical segment / spherical cap, spherical layer,
not identical to the h in the sketch below) |
|
| Volume of a spherical cap | |
| Area of a spherical cap | |
| Lateral surface of a spherical layer | |
| Moment of inertia of a hollow sphere (axis of rotation through center point) | |
| Moment of inertia of a full sphere (axis of rotation through center point) |
volume
The spherical volume is the volume of a sphere that is limited by the spherical surface.
Cone derivation (Archimedean derivation)
According to a thought by the Greek mathematician Archimedes, there is a reference body for a hemisphere with a radius whose volume corresponds to that of the hemisphere, but is easy to calculate. This comparison body arises from the fact that one of a cylinder (more precisely, a right circular cylinder) with base surface radius and height of a cone (more precisely, a right circular cone) with base surface radius and height away.
To prove that the hemisphere and the reference body have the same volume, one can use Cavalieri's principle. This principle is based on the idea of dividing the observed bodies into an infinite number of slices of infinitesimal (infinitely smaller) thickness. (An alternative to this method would be to use integral calculus .) According to the principle mentioned, the intersection surfaces with the planes that are parallel to the respective base surface and have a predetermined distance from it are examined for both bodies .
In the case of the hemisphere, the cut surface is a circular surface. The radius of this circular area results from the Pythagorean theorem :
- .
This gives for the content of the cut surface
- .
In the case of the reference body, however, the cut surface is a circular ring with an outer radius and an inner radius . The area of this cut surface is accordingly
- .
For any distance to the base, the two cut surfaces therefore have the same surface area . With the Cavalieri principle it follows that the hemisphere and the reference body have the same volume.
The volume of the reference body and thus also of the hemisphere can now be easily calculated:
The cone volume is subtracted from the cylinder volume.
Therefore the following applies to the volume of the (full) sphere:
- .
Alternative derivation
The sphere can be divided into an infinite number of pyramids with height (points in the center of the sphere), the entire base area of which corresponds to the surface of the sphere (see below). So that the entire volume of all pyramids .
Derivation with the help of the integral calculus
Radius in distance :
- .
Circular area at a distance :
- .
Volume of the sphere :
- .
In the same way one can calculate the volume of a spherical segment of the height :
- .
Further derivations
A sphere with a radius whose center is in the coordinate origin can be expressed by the equation
describe, where the space coordinates are.
This problem can be solved in two ways using integral calculus:
We parameterize the sphere down to a Lebesgue null set
- .
With the functional determinant
the required volume element results as
- .
The volume of the sphere is therefore given as
Another possibility is via the polar coordinates:
Now the Cartesian coordinate system is transformed into the polar coordinate system, which means that the integration is continued after the “change” of the coordinate system by means of the variables and instead of by and as before . The motivation for this transformation is the considerable simplification of the calculation in the further course. For the differential this means: (keyword: surface element )
Further way with the help of the formula for solids of revolution
If you let a piece of surface rotate around a fixed spatial axis, you get a body with a certain volume. A sphere is created in the case of a circular area. One can visualize this as a rotating coin.
The general formula for solid bodies of revolution that rotate around the x-axis gives
- .
The equation for the circle is
with focus
- .
Plugged into the equation for the circle we get
- .
By inserting it into the formula for rotating bodies around the x-axis, you get
surface
The spherical surface is the two-dimensional area that forms the edge of the sphere. So it is the set of all points whose distance from the center of the sphere has a fixed value . It is a closed, two-dimensional manifold .
Its surface area is and therefore the same size as that of the outer surface of the circular cylinder that envelops the sphere.
For a given volume, the sphere has the smallest surface of all possible bodies.
Reason
If you divide a sphere into:
- Layers with a height of and respectively
- “ Meridians ” that are also at a distance from one another at the equator
and allowed to aspire
- so the length of each field is inversely proportional to - that is, to its distance from the central axis.
- This becomes clear from the drawing above on the right: is the distance between the tangential point and the central axis. The tangent is perpendicular to the “spoke” and the two (right-angled) triangles are similar to each other . Hence:
- .
- The width of each field, however, is proportional to .
- This can be seen directly from the drawing below, "Top view".
The length multiplied by the width is therefore always the same, i.e. H. all square fields have the same area.
The surface area is at the equator ( which against sought because at the equator faster against pursued as compared ).
So as all the content fields have and total (number of fields in the horizontal direction multiplied by the number of fields in the vertical direction, that is) are fields, the total area of all fields is: .
Alternative derivation using the spherical volume
A sphere can be imagined composed of an infinite number of infinitesimal (infinitely small) pyramids . The bases of these pyramids together form the spherical surface; the heights of the pyramids are each equal to the radius of the sphere . Since the pyramid volume is given by the formula , a corresponding relationship applies to the total volume of all pyramids, i.e. the spherical volume:
- ( = Total surface of the sphere)
Because of :
Alternative derivation using the spherical volume and differential calculus
Since the sphere volume with
is defined and on the other hand the surface a change in volume loudly
is, the surface formula results immediately from the derivation of the volume formula.
Derivation with the help of the integral calculus
From the first Guldin rule
for the lateral surface of a solid of revolution results:
Derivation with the help of the integral calculus in spherical coordinates
For the surface element on surfaces = constant, the following applies in spherical coordinates:
- .
This makes it easy to calculate the surface:
properties
- The sphere has an infinite number of planes of symmetry , namely the planes through the center of the sphere. Furthermore, the ball is rotationally symmetrical with respect to each axis through the center point and each angle of rotation and point-symmetrical with respect to its center point.
- The sphere has neither edges nor corners. Its surface cannot be spread out in the plane without distortion, see also the article map network design .
- In differential geometry , a radiused sphere has Gaussian curvature at every point on the surface . This also means that the sphere cannot be mapped onto the plane (curvature 0) without distortion.
- The shortest distance between two points on the surface of the sphere ( geodesic ) lies on a great circle , i.e. a circle through the center of the sphere. Geodesics on the globe, for example, lie on the longitudes, but not on the latitudes - with the exception of the equator.
- With the stereographic projection , the sphere can be mapped bijectively onto the plane , except for the “North Pole” . This allows z. B. the four-color theorem can be transferred to the sphere. With the reverse mapping, the plane can be mapped bijectively onto the spherical surface without the "north pole", the "north pole" then stands for the "infinitely distant point" . In function theory , the complex number plane is transferred to the sphere in this way ( Riemannian number sphere ), making it a compact Riemannian surface of gender 0.
- The sphere has the smallest surface area of all bodies with a given volume. Of all bodies with a given surface, it encloses the largest volume. For this reason, the sphere also occurs in nature: bubbles (see soap bubble ) and water droplets are spheres (without taking gravitation into account ) because the surface tension tries to minimize the surface. Planets are approximately spheres because they were liquid when they were formed and the sphere is the shape with the greatest gravitational binding energy . The mathematical sphere is an ideal shape. Balls occurring in nature are always approximately spherical.
- The ratio of the volume of a sphere with a radius to the volume of the circumscribed cylinder (radius , height = , see picture) is . This , as well as the surface and volume formulas, were already known to the Greek Archimedes in ancient times.
- A sphere can also be understood as a solid of revolution: If you let a semicircular surface rotate around its diameter , a sphere is created. If the circle is replaced by an ellipse that rotates around one of its axes, the result is an ellipsoid of revolution (also called a spheroid ).
- The ball automatically rolls down an inclined plane or it can be rolled in all directions on a surface by the action of external forces . In technology, industrially manufactured (ground) balls have been found in deep groove ball bearings since the 19th century .
generalization
Higher-dimensional Euclidean spaces
The concept of the sphere can be transferred to rooms of other dimensions . Analogous to the three-dimensional solid sphere, a ‑ dimensional sphere is defined for a natural number as the set of all points in ‑ dimensional Euclidean space whose distance to a given point (the center point) is less than or equal to a positive real number (the radius). The edge of the ‑ dimensional sphere, ie the set of all points whose distance from the center is the same , is called the ‑ dimensional sphere or short ‑ sphere . If you no further details of the dimensional sphere speaks, it usually means the dimensional unit sphere ; in this case the center point is at the origin of the coordinate system and the radius is equal to 1.
According to this definition, a three-dimensional sphere is an ordinary sphere; their surface corresponds to a 2 ‑ sphere. A two-dimensional sphere is a circular area, the corresponding circular edge is a 1-sphere. Finally, a one-dimensional sphere is a line , whereby the two end points of the line can be understood as a 0-sphere.
Note: These terms are not used consistently. Spheres in the sense of the definition given here are sometimes called spheres. In addition, some authors speak of -spheres when they mean -dimensional spheres in -dimensional space.
The -dimensional volume of a -dimensional sphere with radius is
- .
Here is the gamma function , a continuous expansion of the faculty . The ‑ dimensional content of the ‑ dimensional surface, i.e. the sphere, is obtained by deriving the volume according to the radius:
- .
For a unit sphere in dimensions one finds the following volumes and surface areas:
| Dimensions | 1 | 2 | 3 | 4th | 5 | 6th | 7th | 8th | 9 | 10 | ... | 2n | 2n + 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| volume | 2 | ... | |||||||||||
| surface | 2 | ... |
A -sphere is an example of a compact - diversity .
Metric spaces
The concept of the sphere can be generalized to all spaces in which one has a concept of distance, that is, the metric spaces .
Is a metric space, and , so called
the open sphere with center and radius . The amount:
is called closed sphere .
Some authors also write for the open and closed spheres. Other spellings for the open spheres are and .
Closest packing of spheres
The closest packing of spheres is the mutual arrangement of spheres of equal size that takes up the smallest space . The empty space between the densely packed spheres only takes up about 26% of the total space, or the packing density is about 74% :
- .
This arrangement can be described in two ways:
It consists of flat layers of touching spheres,
- each of which is touched by six neighboring balls and by three balls each from the layer above and from the layer below, or
- each of which is touched by four neighboring balls and by four balls each from the layer above and from the one below.
The first of the two descriptions is the preferred one. The layer contained therein is called a hexagonal (regularly hexagonal) sphere layer , which in the second case is called a tetragonal (square) sphere layer .
symbolism
The spherical shape has always been regarded as the "perfect shape". It was only since the advent of the turning techniques that it was almost perfectly possible to produce - at least from wood or soft stone. Later it became a symbol of infinity (sometimes also of the cosmos). With the advent of firearms, cannon and rifle bullets became the epitome of strength and power (see also: bullet (heraldry) ).
Application examples
Earth, moon and mars
The Earth, the Moon and Mars are roughly shaped like a sphere.
earth
The earth has a mean diameter of 12742 km, i.e. the mean radius . The mass of the earth is about 5.9724 · 10 24 kg. Using the above formulas for volume , mean density and surface, this results in :
- Volume :
- Medium density :
- The earth has on average about five and a half times as high a density as water under standard conditions .
- Surface :
moon
The moon has a mean diameter of 3474 km, i.e. the mean radius . The mass of the moon is about 7.346 · 10 22 kg. This results in:
- Volume :
- That's about 2.0 percent of the Earth's volume .
- Medium density :
- The average density of the moon is 3.3 times that of water under standard conditions .
- Surface :
- That's about 7.4 percent of the earth's surface .
Mars
Mars has a mean diameter of 6780 km, i.e. the mean radius . The mass of Mars is about 6.417 · 10 23 kg. This results in:
- Volume :
- That's about 15.1 percent of the Earth's volume .
- Medium density :
- Mars has, on average, a density almost four times as high as water under standard conditions .
- Surface :
- That's about 28.4 percent of the earth's surface .
The soccer ball and other balls
A soccer ball is spherical and has a circumference of around 68 centimeters , i.e. a radius of . The mass of a soccer ball is about 410 grams . This results in:
- Volume :
- Medium density :
The following table shows the circumference , volume , mass and mean density (approximate values) of different balls in comparison:
| scope | volume | Dimensions | Medium density | |
|---|---|---|---|---|
| Soccer | 68 cm | 5.28 · 10 −3 m 3 | 410 g | 78 kg / m 3 |
| Handball | 58 cm | 3.29 · 10 −3 m 3 | 425 g | 129 kg / m 3 |
| basketball | 74.9 cm | 7.10 · 10 −3 m 3 | 567 g | 80 kg / m 3 |
| volleyball | 65 cm | 4.64 · 10 −3 m 3 | 260 g | 56 kg / m 3 |
| Tennis ball | 20.5 cm | 0.146 · 10 −3 m 3 | 56.7 g | 388 kg / m 3 |
| Ping pong ball | 12.6 cm | 0.0335 · 10 −3 m 3 | 2.7 g | 81 kg / m 3 |
| Golf ball | 13.4 cm | 0.0407 · 10 −3 m 3 | 45.9 g | 1128 kg / m 3 |
| Billiard ball | 18.0 cm | 0.0980 · 10 −3 m 3 | 170 g | 1735 kg / m 3 |
See also
- Great circle
- sphere
- Spherical Geometry • Spherical Trigonometry
- Spherical triangle • Spherical triangle
- Spherical segment • spherical cutout • spherical layer
- Sphere (descriptive geometry)
- Unit sphere
The bullet in literature
In the novel Kryonium. The experiments of memory by Matthias AK Zimmermann is the formula for calculating a spherical volume (4/3 · π · r³) at the center of the story; it is clearly explained to the reader. The novel is dedicated to Archimedes , who derived this formula. The main character gets into a world of oblivion and darkness, which is made up of numerous elements of mathematics. The story revolves around an enchanted 1001-piece snow globe collection that guides the mysterious processes in a castle. Various references to mathematics can be found in the novel, such as a winter forest that is curved like a Möbius strip, a monster made of fractal , a Cartesian coordinate system , number palindromes , Latin squares , the dual system , Leonhard Euler and Ada Lovelace .
literature
- Yann Rocher (Ed.): Globes. Architecture et sciences explorers le monde. Norma / Cité de l'architecture, Paris 2017.
- Rainer Maroska, Achim Olpp, Claus Stöckle, Hartmut Wellstein: Intersection 10. Mathematics . Ernst Klett Verlag, Stuttgart 1997, ISBN 3-12-741050-6 .
- Fischer / Kaul: Mathematics for Physicists. Springer, 4th edition, ISBN 978-3-662-53968-2 .
Web links
- Everything about the sphere
- Sphere Volume Java applet (requires Java 1.4 installation)
- Derivation of the volume formula for spheres using the Cavalieri principle
Individual evidence
- ^ Boto von Querenburg: Set theoretical topology. Springer-Verlag, Berlin / Heidelberg 1976, definition 1.3. 3rd edition 2001, ISBN 3-540-67790-9 .
- ^ Herbert Federer : Geometric Measure Theory. Springer-Verlag, Berlin / Heidelberg 1969, 2.8.1.
- ↑ te: c-science.com: joint derivation of the packing density for face-centered cubic and hexagonal densely packed lattices , together
- ^ Siegfried Wetzel: Dense packing of spheres ; 8. The crystallographic unit cells and their packing densities ; separate calculation for face-centered cubic and hexagonal unit cells
- ↑ Tóth, László Fejes: densest spherical packing , treatises of the Braunschweigischen Wissenschaftlichen Gesellschaft Volume 27, 1977, p. 319
- ↑ Literaturkritik.de reference to Archimedes of Syracuse
- ↑ Berliner Gazette: In der Schneekugel: How literature can remember, create and re-measure virtual spaces
- ↑ Aargauer Zeitung: Caught in the infinite virtuality





























































![{\ displaystyle V = \ pi r ^ {2} \ left [x \ right] _ {- r} ^ {r} - {\ frac {1} {3}} \ pi \ left [{x ^ {3} } \ right] _ {- r} ^ {r}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6a0bdfef74621c05105237e5ad5307e46541426)
![{\ displaystyle V = \ pi r ^ {2} \ left [r - (- r) \ right] - {\ frac {1} {3}} \ pi \ left [r ^ {3} - (- r) ^ {3} \ right] = 2 \ pi r ^ {3} - {\ frac {2} {3}} \ pi r ^ {3} = {\ frac {4} {3}} \ pi r ^ { 3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8e8b644c410efef3c860f803151b559f0e5b561)

![V _ {\ mathrm {KS}} = \ int _ {rh} ^ {r} {A_ {x} \, \ mathrm {d} x} = \ pi r ^ {2} \ left [x \ right] _ { rh} ^ {r} - {\ frac {1} {3}} \ pi \ left [{x ^ {3}} \ right] _ {rh} ^ {r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e3eac1232a18271d5315396f1a3962d66b8b799)
![V _ {\ mathrm {KS}} = \ pi r ^ {2} \ left [r- (rh) \ right] - {\ frac {1} {3}} \ pi \ left [r ^ {3} - ( rh) ^ {3} \ right] = \ pi r ^ {2} h - {\ frac {1} {3}} \ pi \ left [r ^ {3} - (r ^ {3} -3r ^ { 2} h + 3rh ^ {2} -h ^ {3}) \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2542735740c1db5826e1eb8a38e772457d4602ca)















![{\ begin {aligned} \ int _ {K} \! \ mathrm {d} V & = \ int \ limits _ {0} ^ {2 \ pi} \ int \ limits _ {0} ^ {R} 2 {\ sqrt {R ^ {2} -r ^ {2}}} \; r \, \ mathrm {d} r \, \ mathrm {d} \ varphi \\ & = 2 \ pi \ int \ limits _ {0} ^ {R} 2 {\ sqrt {R ^ {2} -r ^ {2}}} \; r \, \ mathrm {d} r \\ & = 2 \ pi (-1) {\ frac {2} {3}} \ left [{\ sqrt {(R ^ {2} -r ^ {2}) ^ {3}}} \ right] _ {r = 0} ^ {R} \\ & = {\ frac {4} {3}} \ pi R ^ {3}. \ End {aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c23fd89b7df891c3613bd42210631ffcea85c2f)
![V = \ pi \ int _ {a} ^ {b} [f (x)] ^ {2} \ mathrm {d} x = \ pi \ int _ {a} ^ {b} y ^ {2} \, \ mathrm {d} x](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c6c7a545aea40bde71da9577c4d2460ad61d66)



![{\ displaystyle {\ begin {aligned} V _ {\ text {sphere}} & = \ pi \ int _ {- r} ^ {r} \ left (r ^ {2} -x ^ {2} \ right) \ , \ mathrm {d} x \\ & = \ pi \ left [r ^ {2} x - {\ frac {1} {3}} x ^ {3} \ right] _ {- r} ^ {r} \\ & = \ pi \ left (r ^ {3} - {\ frac {1} {3}} r ^ {3} \ right) - \ pi \ left (r ^ {2} \ cdot (-r) - {\ frac {1} {3}} (- r) ^ {3} \ right) \\ & = \ pi \ left [\ left ({\ frac {2} {3}} r ^ {3} \ right) - \ left (- {\ frac {2} {3}} r ^ {3} \ right) \ right] \\ & = {\ frac {4} {3}} \ pi r ^ {3}. \\\ end {aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b849b51779abd5f1ca4d58f5835dca5cade18f6)




























































































