vector
In the general sense in linear algebra , a vector ( lat. Vector "carrier, driver") is an element of a vector space , that is, an object that can be added to other vectors and multiplied by numbers called scalars . Vectors in this general sense are discussed in the article vector space .
In the narrower sense, in analytical geometry , a vector is understood to be a mathematical object that describes a parallel displacement in the plane or in space. A vector can be represented by an arrow that connects an original image point with its image point. Arrows that are of the same length, parallel and oriented in the same way describe the same vector. In Cartesian coordinates , vectors are represented by number pairs (in the plane) or triples (in space), which are often written below one another (as "column vectors"). Vectors can be added and multiplied with real numbers ( scalars ).
Motivated by the coordinate representation of geometric vectors are often - tuples of real numbers, that is, elements of , called vectors or as coordinate vectors. This is justified by the fact that every -dimensional real vector space is isomorphic to the vector space . Examples of such a use of the term vector can be found in business mathematics .
This article mainly deals with vectors in the geometric sense and with vectors as elements of the "tuple space" .
Vector quantities in physics are closely related to geometric vectors . These are physical quantities that have a magnitude and a direction and are often represented by arrows whose length corresponds to the magnitude of the quantity. Examples are speed , acceleration , momentum , force , electric and magnetic field strength .
history
Vector calculation was founded by Hermann Günter Graßmann , who published his Lineale Expansion Theory in 1844 , a book with more than three hundred pages. The forerunners include: a. René Descartes and August Ferdinand Möbius , a student of Carl Friedrich Gauß . Around 1850 the Irish mathematician Matthew O'Brien used vector calculus to describe mechanical facts, but was largely ignored. Almost at the same time William Rowan Hamilton developed his similar theory of quaternions , which he published in 1853 in the book Lectures on Quaternions and in 1866 in the work Elements of Quaternions . In Germany, vector computation became particularly popular through lectures and books by Alfred Bucherer , August Föppl , Carl Runge , Fischer, v. Ignatowsky and Richard Gans spread.
Spelling and speaking styles
Variables that stand for vectors are often marked with an arrow, especially in school mathematics and physics ( ). Especially in English-speaking countries, they are also written in bold ( , or v ). In manuscripts this is often represented by underlining ( ) or something similar. In the past, the spelling with small Fraktur letters ( ) was also common, handwritten using German cursive or Sütterlin script. Frequently chosen letters are and . The corresponding Latin letter without vector marking usually stands for the length (the amount) of the vector:
geometry
definition
In geometry , a vector is an object that describes a parallel displacement in a plane or in space. A shift can be represented by an arrow that connects an original image point with its image point. Arrows that are parallel, of the same length and of the same direction describe the same displacement and thus represent the same vector. For example, in the picture on the right, the arrow from to , the arrow from to and the arrow from to describe the same displacement by 7 units to the right and 3 units up. They all represent the same vector . Formally, therefore, vectors can be defined as follows:
- An arrow is a directed route, that is, a route for which an order of the end points is specified. Two arrows are equivalent if they are parallel, of the same length and of the same direction. This defines an equivalence relation on the set of arrows of the plane or of the space. The equivalence classes are called vectors.
Another possibility is to identify a vector with the parallel displacement represented by it . "Vector" is then just another way of speaking for "parallel shift".
The vector describing a displacement that maps the point to the point is written as and graphically represented by an arrow pointing from point to point . One says: "The vector maps up ", or: "The vector connects and ." In this case, the point is referred to as the shaft, starting or starting point and the tip or end point of the vector arrow. The distance between the two points is called the length or magnitude of the vector.
The reverse vector that with links, is counter-vector to . The vector that maps a point onto itself is called the zero vector and is denoted by or . It is the only vector that cannot be graphically represented by an arrow.
Location and direction vectors
Vectors can also be used to denote points in space. So the location of the point can be given by the vector
being represented. This vector is called the position vector belonging to the point . It denotes the origin of coordinates , which forms the starting point for all position vectors.
To distinguish them from them, vectors, as described in the previous section, are also referred to as direction vectors . Two direction vectors are identical if they have the same magnitude and direction. However, as shown, you can have any point in space as a starting point, while position vectors always start from the origin of coordinates.
This distinction is important in analytical geometry, among other things. There, for example, a straight line is described by the following equation:
The support vector is the position vector of an arbitrarily chosen “support point” of the straight line. The direction vector indicates the direction of the straight line. Because stands for any real number, is the position vector of any point on the straight line.
Representation in coordinates
If, as in the figure above, a straight-line coordinate system is given, a vector of the plane can be described by an ordered pair of numbers, a vector in space by a number triple. As a rule, these coordinates are written below one another as so-called column vectors . For the vector in the plane that describes the shift by 7 units to the right (in the direction) and 3 units upwards (in the direction), one writes . The vector describes a shift by 2 units in the -direction and −5 units in the -direction, i.e. by 2 units to the right and 5 units downwards. Correspondingly, the vector describes a shift by 3 units in the -direction, 2 units in the negative -direction and 4 units in the -direction.
The coordinates of a vector can be calculated as the difference between the coordinates of the end and starting point. In the example above, and have the coordinates and . The coordinates of the connection vector are then calculated as follows:
Amount and direction
In contrast to scalars , vectors have a direction. A vector is characterized by its magnitude and direction. The direction is given on the one hand by the axis position and on the other hand by the sense of direction . The sense of direction indicates in which of the two directions along the axis the vector is pointing. A change in sign in the size of the vector corresponds to the reversal of the sense of direction.
Arithmetic operations
Addition and subtraction
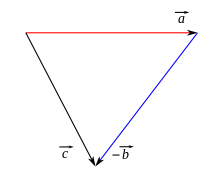
The addition of two geometric vectors corresponds to the execution of the associated shifts one after the other. , The vector , the displacement is that the point on forms maps, and to shift the corresponding point on starting, so describes the shift of maps:
Geometrically, two vectors and can therefore be added by representing the two vectors with arrows so that the starting point of the second arrow coincides with the end point of the first arrow. The sum is then represented by the arrow from the start point of the first to the end point of the second arrow.
Alternatively, the two vectors are represented by arrows with a common starting point and this figure is expanded to form a parallelogram . The diagonal arrow from the common starting point to the opposite corner then represents the sum of the two vectors. In physics , this construction is used for the parallelogram of forces .
The sum is calculated component-wise in coordinates: For the sum of the two vectors
- and
applies
- .
The associative and commutative laws apply to the addition of vectors .
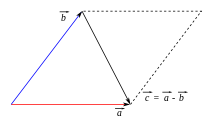
For the difference between two vectors and applies
- .
It can be interpreted geometrically in two ways:
- As the sum of with the opposite vector of . The starting point of an arrow, which represents the opposite vector of , is placed at the end point of the arrow, which represents.
- As the vector that just gives to added . If and are represented by arrows with the same starting point, then the arrow that leads from the end point of the second vector to the end point of the first vector is shown.
If two vectors are added (subtracted), their amounts are only added (subtracted) if the vectors are collinear and have the same orientation. In the general case, however, the triangle inequality applies :
Multiplication by a scalar
Vectors can be multiplied with real numbers (often called scalars to distinguish them from vectors) ( scalar multiplication , also called S multiplication):
The length of the resulting vector is . If the scalar is positive, the resulting vector points in the same direction as the original, if it is negative, in the opposite direction.
The distributive law applies to vector addition and multiplication by a scalar :
The same applies to the addition of two scalars:
Scalar product
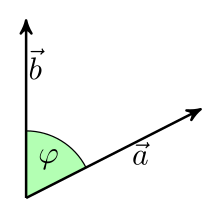
The scalar product (or inner product ) of two vectors and so called because the result is a scalar, is noted as or and is
where is the angle enclosed between the two vectors (see also cosine ). Are the two vectors at right angles to each other, so as true.
In the Cartesian coordinate system, the scalar product is calculated
especially applies to the square of a vector
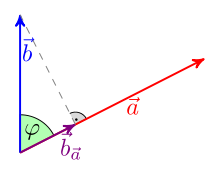
Geometrically, the scalar product can also be understood as follows (see figure): One projects one vector perpendicularly onto the other and thus obtains the vector . If the angle enclosed by the two vectors is an acute angle, points in the same direction as . In this case the scalar product results from the multiplication of the two amounts of and . This number is positive. If it is, however, by an obtuse angle, so the projection of anti-parallel to and, therefore, the dot product has a negative sign. If the two vectors enclose a right angle ( ), then the length of the projected vector is zero and thus also the scalar product. (If you swap the two vectors when doing this, the result is the same value.)
This operation is often used in physics , for example to calculate the work when the direction of the force does not coincide with the direction of movement.
The commutative law applies to the scalar product
and the distributive law
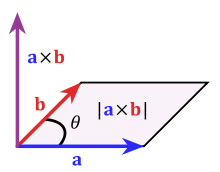
Cross product
The cross product (also vector product, outer product or vector product ) (spoken as “a cross b”) of two vectors in the three-dimensional Euclidean vector space is a certain vector that is perpendicular to the plane spanned by and . The length of this vector is equal to the area of the parallelogram with the sides and , so
where the angle enclosed by the two vectors is denoted here by . The cross product of two collinear vectors therefore gives the zero vector.
In the three-dimensional Cartesian coordinate system, the cross product can be calculated as follows:
The cross product is anti-commutative , i.e. i.e., it applies
Late product
The combination of cross and scalar product in the form
is called a late product. The result is a scalar. Its amount is the volume of the spat that is spanned by the three vectors. If the three vectors form a legal system , then is positive. If they form a left system , it is negative. If the vectors are linearly dependent, then applies .
Length / amount of a vector
In Cartesian coordinates, the length of vectors can be calculated according to the Pythagorean theorem :
This corresponds to the so-called Euclidean norm . The length can also be specified in an alternative notation as the root of the scalar product:
Vectors of length 1 are called unit vectors . If a vector has the length 0, it is the zero vector.
With vector quantities in physics, one speaks of the amount of a vector instead of the length . A vector physical quantity can be viewed as a pair of the direction of the quantity as a unit vector and the magnitude of the quantity along this direction. The unit of the amount is the same as the unit of the physical quantity. For example, the speed
of a helicopter flying at constant altitude in a south-easterly direction
and
represent. The amount of the path speed for the horizontal throw (start speed in -direction , current speed in -direction ) can be specified as
Dyadic product
The dyadic or tensorial product or (spoken as “a dyadic b”) of two vectors forms a dyad. With dyads, a vector can be mapped linearly onto another vector, see picture. The portion of a vector in the direction of the vector is brought in the direction of the vector and stretched or compressed. The mapping is done with the above scalar product:
In the three-dimensional Cartesian coordinate system, the dyadic product can be calculated as follows:
The dyadic product is not commutative; i.e., in general
but distributive with vector addition:
It is also compatible with scalar multiplication:
The dyadic product creates a new class of objects of linear algebra , the matrices and linear mappings , depending on whether calculations are carried out in coordinate space or vector space . Linking multiple dyads (as in ) creates higher level dyads. Dyads are a special case of tensors . Tensors play an important role in continuum mechanics , the Maxwell equations of electromagnetism and general relativity . The formula collection Tensalgebra gives an overview of the tensor algebra .
Component notation
As an alternative to the notation presented here as column vectors, vectors can also be represented in component notation. Usually stands for the individual components of the vector with respect to the standard basis . This means that the arithmetic operations can be written as follows with regard to the standard basis:
| Column vectors | Component notation | |
|---|---|---|
| Addition / subtraction | ||
| Scalar product |
respectively: |
|
| amount |
respectively: |
|
| Cross product |
respectively: |
- ↑ a b c Using Einstein's summation convention
- ↑ is the Levi-Civita symbol and is +1 for even permutations of (1, 2, 3), −1 for odd permutations and 0 otherwise.
See also the section #Coordinates and components of a vector below.
n tuples and column vectors
In generalization of the coordinate representation of geometric elements are vectors of so - tuples of real numbers , called vectors, when the typical vectors arithmetic operations of addition and scalar multiplication are executed with them. As a rule, the tuples are written as so-called column vectors , that is, their entries are one below the other.
Addition and scalar multiplication
The addition of two vectors and the scalar multiplication of a vector by a number are defined component by component:
With these connections, the set forms a vector space over the body . This so-called coordinate space is the standard example of a -dimensional -vector space.
Standard scalar product
The standard scalar product is defined by
- .
With this scalar product it is a Euclidean vector space .
Multiplication by a matrix
If there is a ( ) matrix and a column vector, then one can understand as a single column matrix and form the matrix-vector product . The result is a column vector in :
The multiplication with a ( ) matrix is a linear mapping from to . Every linear mapping can be represented as a multiplication with a matrix.
Length or norm
The length or norm of a vector is given by the square root of the scalar product with itself:
In addition to this Euclidean norm , other norms are also used, see p norm .
Row and Column Vectors
If one considers vectors as matrices, then a matrix is a column vector
to which there is a matrix
as the corresponding row vector , where the transpose of is. In this notation, the standard scalar product is nothing more than the matrix product of a matrix with a matrix:
The dyadic product is the matrix product of a matrix with a matrix and then yields a matrix:
Properties of vectors
Linear dependency
Vectors ( ) are called linearly dependent if there is a solution for the following equation that does not hold for all coefficients :
If, however, no coefficients can be found that meet this condition, then the vectors are called linearly independent .
The zero vector is linearly dependent, every other vector is linearly independent.
For , in the case of linear dependence, at least one of the vectors can be represented as a linear combination of the others.
In order to define a coordinate system for a -dimensional space, one needs exactly linearly independent basis vectors . Then each vector of this space can be written in a unique way as a linear combination of the basis vectors. More than vectors in -dimensional space are always linearly dependent.
Collinearity of two vectors
Two linearly dependent vectors and are also called collinear . In three-dimensional space applies to them
Each vector is collinear with the zero vector. But if there are two vectors different from the zero vector, then they are collinear if and only if
for one is met. They are parallel when positive and anti-parallel when negative.
Orthogonality
Two vectors and are orthogonal if their scalar product is 0:
For geometric vectors with positive length this means that they enclose a right angle , see scalar product . The zero vector is orthogonal to each vector.
Normalization
A vector (read “a roof”) is called a unit vector or normalized if it has the length 1. A vector is normalized by dividing it by its length, i.e. i.e., multiplied by the reciprocal of its length:
The vector has the same direction as , but length 1. Other notations for are , or .
Unit vectors are important when representing coordinate systems .
Coordinates and components of a vector
The most common coordinate system, the Cartesian , is e.g. As an orthonormal system because it of the three mutually orthogonal unit vectors , and the default base is clamped. The coordinates of a vector are then the scalar products of the vector with the basis vectors:
So every vector can be represented as a linear combination of the basis vectors by writing it as the sum of its components with respect to the basis:
By changing to a different orthonormal basis , the vector gets different coordinates and different components:
More generally three arbitrary but linearly independent vectors can be used as the vector space basis.
Generalizations
The definition of the vector in linear algebra as an element of a vector space is a much more comprehensive one, which, in addition to the conventional, geometric vectors , includes a wide variety of mathematical objects ( numbers , sequences , functions and transformations ).
On the other hand, vectors are just one-step tensors ; H. Tensors with only one index.
Vectors in physics
Vector quantities in the Euclidean space of our view
In classical physics , physical quantities, which have a magnitude and a direction , are understood as vectors of Euclidean space . Examples of this are the location, the speed , the acceleration , the force , etc. They can be compared with scalar physical quantities that only have a magnitude but no direction, such as B. Volume , mass , charge , temperature , etc.
This view of directed physical quantities as vectors is an application of geometric vectors. The direction of the physical quantity takes the place of the shift direction. Their amount corresponds to the displacement of a geometric vector. The representation of such quantities by arrows of a certain length illustrates both their direction and their magnitude. Consequently, everything that has already been said about geometric vectors also applies to vector quantities in physics, in particular what has been said about arithmetic operations and graphic illustration.
Physical quantities can only be added if they are of the same type of quantity . This also applies if you regard them as vectors. The addition is z. B. illustrated by the parallelogram of forces . Vector sums are of outstanding importance in statics , e.g. B. in the definition of the balance of forces .
The dot product is used when the projection of one vector in the direction of another is important. For example, the physical term work means the product of a force and a path in the direction of the force. That is why the work is calculated using the scalar product of the force and the path. In addition, the scalar product is important in the component decomposition of a vector. The cross product, on the other hand, is used wherever a law follows the three-finger rule , e.g. B. Lorentz force or torque . For both the scalar product and the cross product, the unit of the resulting physical quantity is obtained by multiplying the units of both factors.
If a physical vector is itself a function of the location, one speaks of a vector field . It can be illustrated by field lines , the tangent to the field line indicating the direction of the vector. The amount of the vector is represented by the density of the field lines. Examples are the electric and magnetic fields as well as the velocity fields in currents . In the mathematical treatment of the fields, vector analysis proves to be an extremely important tool, e.g. B. in electrodynamics or in fluid mechanics .
Vectors in non-Euclidean spaces in relativistic physics
In the place of the three-dimensional Euclidean space comes the non - Euclidean four - dimensional space - time in the theory of relativity . Vector quantities such as the speed of four or the impulse of four are represented here as four-dimensional vectors .
Transformation behavior of vectors
In physics, vectors are (also) characterized by their transformation behavior when changing reference systems .
Polar and axial vectors
Depending on the transformation behavior under point reflections of the location, a distinction is made between polar and axial vectors , also called thrust and rotation vectors in the older literature: In Euclidean vector spaces, each vector changes into its negative in spatial point reflection, while axial vectors remain unchanged. For example, the location, the speed, the momentum and the electric field change their sign in the case of spatial point reflection , but not the angular momentum or the magnetic field. Polar and axial vectors are elements of different vector spaces because of their different transformation behavior. The cross product must be viewed as a bilinear mapping of two vector spaces into a third.
This view in physics depends on whether you are working in Euclidean or non-Euclidean space.
Transformation behavior in the Euclidean and Minkowski space
For the physical concept of vector, the transformation behavior under the isometric group of the corresponding metric of the underlying space is important. The three-dimensional space of classical mechanics is modeled as Euclidean flat space, while the four-dimensional spacetime of the theory of relativity is provided as Minkowski space with a curved metric. These spaces are manifolds in which vectors represent contravariant tensors of the first order, which determines their transformation behavior. The isometric groups are the rotation group in Euclidean space and the Lorentz group in Minkowski space .
Not all vectors in three-dimensional are parts of four-vectors. The angular momentum transforms under Lorentz transformations, for example, not like part of a four-vector, but together with the initial energy center like the six components of an antisymmetric tensor . Likewise, the electric and magnetic field strength transform like the six components of an antisymmetric tensor.
Many-particle systems with particles are described with vectors in -dimensional vector spaces on which the three-dimensional rotating group acts separately.
Further uses of the term vector in physics
Multi- particle systems of particles are described by vectors in -dimensional vector spaces, or - in Hamiltonian mechanics - in -dimensional phase space , which includes not only the position coordinates but also the pulse coordinates. Finally, the states of quantum mechanical systems are represented as vectors in function spaces. The Bra-Ket notation, which was introduced by Paul Dirac , is particularly helpful here.
literature
- Kurt Bohner, Peter Ihlenburg, Roland Ott: Mathematics for vocational high schools - linear algebra - vector geometry. Merkur, Rinteln 2004. ISBN 3-8120-0552-2 .
- Klaus Jänich : Linear Algebra. 10th edition. Springer, Berlin 2004. ISBN 3-540-40207-1 .
- Lothar Papula : Mathematics for Engineers and Natural Scientists. Volume 1. 11th edition, Vieweg, Wiesbaden 2007, ISBN 978-3-8348-0224-8 .
Web links
- Ronny Harbich: vector calculation for high school graduation. At: fabulierer.de.
- Vectors. At: mathe-online.at.
- History of Vectors. At: math.mcgill.ca.
Individual evidence
- ^ Walter Gellert, Herbert Küstner, Manfred Hellwich, Herbert Kästner (Eds.): Small encyclopedia of mathematics. Leipzig 1970, p. 545.
- ↑ [1]
- ↑ Hermann Günter Graßmann: The linear expansion theory a new branch of mathematics: Represented and explained through applications to the other branches of mathematics, as well as to statics, mechanics, the theory of magnetism and crystallonomy . O. Wigand, 1844.
- ↑ Josiah Willard Gibbs: Quaternions and the Expansion Theory . In: Nature . tape 44 , no. 1126 , 1891, pp. 79-82 , doi : 10.1038 / 044079b0 .
- ^ WR Hamilton: Lectures on Quaternions . Hodges and Smith, Dublin 1853.
- ^ WRS Hamilton: Elements of Quaternions: Vol .: 1 . Longmans, Green & Company, 1866 ( Google Books ).
- ^ WRS Hamilton, CJ Joly: Elements of quaternions. Vol .: 2 . Longmans, Green & Company, 1901.
- ^ AEH Love, H. Polster: Theoretical Mechanics. An Introductory Treatise on the Principles of Mechanics . Springer, 2013, ISBN 978-3-642-52592-6 ( limited preview in Google book search).
- ↑ Jessica Scholz: Technical Mechanics 1: Statics. Properties of force. ingenieurkurse.de, accessed on July 31, 2017 .
- ↑ Introduction to vector calculus. Wiley Information Services - Chamgaroo, accessed July 31, 2017 .
- ↑ Raymond A. Serway, John W. Jewett: Principles Of Physics: A Calculus-based Text. Volume 1, Publisher: Cengage Learning, 2006, ISBN 9780534491437 , p. 19, limited preview in Google Book Search
- ^ Lambach Swiss Mathematics for High Schools, course level, Baden-Württemberg. Ernst Klett Verlag, Stuttgart 2009, ISBN 978-3-12-735301-3 , page 243.
- ^ Fritz Reinhardt, Heinrich Soeder: dtv atlas for mathematics. Volume I: Fundamentals, Algebra and Geometry. 3rd edition, Deutscher Taschenbuch Verlag, Munich 1978, p. 191.
- ↑ Grimsehl: Textbook of Physics, Vol. I. Leipzig 1954, pp. 577-578.