Diagonal (geometry)

Diagonal (from ancient Greek διά dia : "through" and γωνία gonia : "corner, angle") is a term from geometry . In general, the term refers to lines that connect the corners of surfaces or bodies without being a side or edge of the figure. For the exact definition see below.

Diagonals in the plane geometry

Seventeen corner with 14 diagonals from a corner
z. B. means : diagonal over three sides ${\displaystyle d_{3}}$

In planar geometry , diagonals are the connecting lines of non-adjacent corners in a polygon (polygon) , which must therefore have at least four corners.

Number of diagonals

The number of diagonals in a corner, i.e. in a polygon with the number of corners , is ${\displaystyle d(n)}$ ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle d(n)={\frac {n(n-3)}{2}}}$,

because each of the corners is connected to corners by a diagonal (not with itself and not with the two neighboring corners). The denominator ( divisor ) 2 in the formula takes into account that, with this consideration, each diagonal would be generated twice with a complete cycle over all corner points. ${\displaystyle n}$ ${\displaystyle n-3}$

This results in the number of corners 3 to 25:

${\displaystyle n}$	3	4th	5	6th	7th	8th	9	10	11	12	13	14th	15th	16	17th	18th	19th	20th	21st	22nd	23	24	25th
${\displaystyle d}$	0	2	5	9	14th	20th	27	35	44	54	65	77	90	104	119	135	152	170	189	209	230	252	275

With a convex polygon , all diagonals lie completely within the polygon, with a concave polygon at least one diagonal lie completely outside the polygon.

Lengths of diagonals

General

The diagonal length from one corner to the next corner is calculated from the length of the two intermediate sides and and the intermediate angle according to the law of cosines : ${\displaystyle d}$ ${\displaystyle s_{0}}$ ${\displaystyle s_{1}}$ ${\displaystyle \varphi _{1}}$

${\displaystyle d={\sqrt {s_{0}^{2}+s_{1}^{2}-2s_{0}s_{1}\cos \varphi _{1}}}}$

If the sides and the interior angles of the corners in between are known for a partial circumference between the ends of the diagonal , the diagonal length can be calculated from this.

If, starting from one diagonal end, the sides are designated with and the interior angle in front of them with : ${\displaystyle s_{i}}$ ${\displaystyle \varphi _{i}}$

• For the diagonal across three sides:

${\displaystyle d_{3}={\sqrt {(s_{0}-s_{1}\cdot \cos(\varphi _{1})+s_{2}\cdot \cos(\varphi _{1}+\varphi _{2}))^{2}+(s_{1}\cdot \sin(\varphi _{1})-s_{2}\cdot \sin((\varphi _{1}+\varphi _{2}))^{2}}}}$

• The following applies to the diagonal across four sides:

${\displaystyle {\begin{aligned}d_{4}^{2}&=(s_{0}-&s_{1}\cdot \cos(\varphi _{1})+s_{2}\cdot \cos(\varphi _{1}+\varphi _{2})-s_{3}\cdot \cos(\varphi _{1}+\varphi _{2}+\varphi _{3}))^{2}\\&+(&s_{1}\cdot \sin(\varphi _{1})-s_{2}\cdot \sin(\varphi _{1}+\varphi _{2})+s_{3}\cdot \sin(\varphi _{1}+\varphi _{2}+\varphi _{3}))^{2}\end{aligned}}}$

• General for a diagonal across pages: ${\displaystyle n}$

${\displaystyle d_{n}={\sqrt {\left(s_{0}+\sum _{i=1}^{n-1}(-1)^{i}\cdot s_{i}\cdot \cos \left(\sum _{k=1}^{i}\varphi _{k}\right)\right)^{2}+\left(\sum _{i=1}^{n-1}-(-1)^{i}\cdot s_{i}\cdot \sin \left(\sum _{k=1}^{i}\varphi _{k}\right)\right)^{2}}}}$

Special cases

For some special cases there are simple formulas for the diagonal length:

• The diagonal lengths of a parallelogram with the side lengths and and the interior angle are: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \alpha }$

${\displaystyle e={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }}}$

and

${\displaystyle f={\sqrt {a^{2}+b^{2}-2ab\cos \alpha }}}$

• For the diagonal length of a rectangle ( ) with the side lengths and therefore applies according to the Pythagorean theorem : ${\displaystyle \alpha =90^{\circ }}$ ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle d={\sqrt {a^{2}+b^{2}}}}$.

Regular polygons

• The diagonal length of a square with side length can be calculated according to ${\displaystyle a}$

${\displaystyle d=a{\sqrt {2}}}$.

• For the diagonal length of a regular pentagon with side length applies ${\displaystyle a}$

${\displaystyle d={\frac {a}{2}}\left(1+{\sqrt {5}}\right)}$

• The following applies for the diagonals over two or three sides in a regular hexagon with side length ${\displaystyle a}$

${\displaystyle d_{2}=a{\frac {\sqrt {3}}{2}}}$   as well   . ${\displaystyle d_{3}=2a}$

• In general, in a regular polygon with side length, the length of the diagonal over sides results as ${\displaystyle a}$ ${\displaystyle k}$

${\displaystyle d_{k}=a\cdot \sin \left({\frac {k\pi }{n}}\right)\cdot \csc \left({\frac {\pi }{n}}\right)}$.

Diagonals in spatial geometry

In stereometry , the diagonal of a polyhedron is understood to be a line that connects two corners of the body with one another, but neither coincides with an edge nor with a diagonal of a side surface (space or body diagonal).

Number of diagonals

To find the number of diagonals of a polyhedron, subtract 1 from the number of corners, multiply the remainder by the number of corners and halve the product . From the number obtained in this way, you first subtract the number of all edges and then the number of diagonals of all side surfaces.

If you denote the number of corners with , the number of surfaces with the number of edges with and the number of corners of the surface no. With one results ${\displaystyle E}$ ${\displaystyle F}$ ${\displaystyle K}$ ${\displaystyle i}$ ${\displaystyle N_{i}}$

${\displaystyle Z={\frac {E(E-1)}{2}}-K-\sum _{i=1}^{F}{\frac {N_{i}(N_{i}-3)}{2}}}$

For all parallelepipeds , e.g. B. cuboid results with

${\displaystyle E=8,\quad F=6,\quad K=12,\quad N_{i}=4\quad \forall i}$:

${\displaystyle Z={\frac {8(8-1)}{2}}-12-\sum _{i=1}^{6}{\frac {4(4-3)}{2}}}$

${\displaystyle Z=28-12-6\cdot 2}$

${\displaystyle Z=4}$

Lengths of diagonals

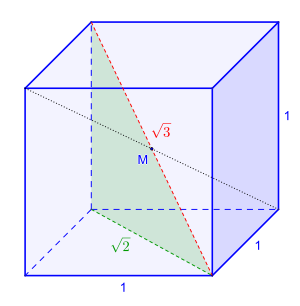
• The length of the space diagonal of a cube (side lengths , , is) . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d={\sqrt {a^{2}+b^{2}+c^{2}}}}$

• This results in the special case of the cube . ${\displaystyle d=a{\sqrt {3}}}$

Diagonal method

Application in art

In the fine arts , diagonals are used as a compositional element for the formal design of works. The diagonal method in particular divides a rectangular format into two squares and then uses their diagonals to arrange the image.

perception

Diagonals in the broader sense of art and (photo) graphic design are perceived differently: Those that rise upwards to the right are perceived as positive and dynamic and therefore referred to as positive diagonals . The opposite pole is the negative diagonal that comes from the top left in the picture and runs to the bottom right - symbol for braking, stopping, negative feelings. Feature good design, it can be to have a diagonal or diagonal structure, the visual statement supporting direction may be faced with a small version of its counterpart, an anti-diagonal . The effect can be explained perceptually psychologically from the direction of writing and reading to the right, the orientation of quickly handwritten letters, italic printers, lines of handwriting that rise upwards according to the movement of the forearm to the top right and graphics from science to the stock market price, if there is a higher right- hand orientation A value plotted upwards develops positively over the time axis running to the right.

See also

• Screen diagonal

Individual evidence

1. ↑ J. Dorfmeister: Consequences and complete induction - model solution. Preliminary course mathematics intensive WS 06/07. In: “11. [...] number d (n) of the diagonals ... " TU Munich, 2006, p. 3 , accessed on September 9, 2018 . 
2. ↑ Hartel, M. (2008). Urban expression. Digital Photographer, 74 (September), 30-42.