pentagon

Regular pentagon

A pentagon, also a pentagon (from ancient Greek πεντάγωνον pentágōnon "pentagon"), is a geometric figure . It belongs to the group of polygons ( polygons ) and is defined by five points defined.

Classification

Pentagons, like all polygons that are not triangles , can be divided into:

• Overturned pentagon: at least two sides intersect.
• concave pentagon: at least one interior angle is greater than 180 °. A pentagon can have a maximum of two such angles .
• convex pentagon: all interior angles are smaller than 180 °
• Chordal pentagon: all corners lie on a common perimeter .
• Regular pentagon: All sides are the same length and all interior angles are the same size. Regular pentagons can be convex or overturned.

General pentagon

angle

The sum of the interior angles of a regular pentagon is 540 °, i.e. 3 times 180 °, and results from a general formula for polygons in which the number of corner points of the polygon must be used for the variable (in this case ): ${\displaystyle n}$ ${\displaystyle n=5}$

${\displaystyle \sum {\alpha =}(n-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }}$

surface

A flat pentagon has a clearly determinable area , which can always be calculated by breaking it down into triangles .

Regular pentagon

Formulas

Mathematical formulas for the regular pentagon
Area	${\displaystyle A={\frac {a^{2}}{4}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\approx 1{,}720\cdot a^{2}}$
height	${\displaystyle h=r_{u}+r_{i}={\frac {a}{2}}\cdot {\sqrt {5+2\cdot {\sqrt {5}}}}\approx 1{,}539\cdot a}$
Length of the diagonal	${\displaystyle d={\frac {a}{2}}\cdot (1+{\sqrt {5}})\approx 1{,}618\cdot a}$
Inscribed radius	${\displaystyle r_{i}={\frac {a}{10}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\approx 0{,}688\cdot a}$
Perimeter radius	${\displaystyle r_{u}={\frac {a}{10}}\cdot {\sqrt {50+10\cdot {\sqrt {5}}}}\approx 0{,}851\cdot a}$
Interior angle	${\displaystyle \alpha =108^{\circ }}$

Visual aid for deriving the adjacent statements about angles

Interior angle

The angle that two adjacent sides enclose in the flat, regular pentagon is (again according to a general formula for regular polygons ):

${\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}$

surface

The area A of a regular pentagon the length of the side is five times the area of ​​a triangle spanned by its center point and two of its corner points. ${\displaystyle a}$

${\displaystyle A=5\cdot {\frac {1}{2}}\cdot a\cdot \tan 54^{\circ }\cdot {\frac {a}{2}}={\frac {5}{4}}\cdot a^{2}\cdot \tan 54^{\circ }\approx 1{,}720\cdot a^{2}}$

Generally with the radius r _u

${\displaystyle A={\frac {5}{8}}\cdot r_{u}^{2}\cdot {\sqrt {10+2\cdot {\sqrt {5}}}}}$

or

${\displaystyle A={\frac {5}{2}}\cdot r_{u}^{2}\cdot \sin {72^{\circ }}\approx 2{,}378\cdot r_{u}^{2}}$

Side length

${\displaystyle a=2\cdot r_{u}\cdot \sin 36^{\circ }}$

or:

${\displaystyle a=r_{u}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}176\cdot r_{u}}$

For conversion see the section on the sine and cosine values that can be specified as square roots .

The golden ratio in the pentagon

Pentagram

The regular pentagon and pentagram form a basic figure in which the relationship of the golden ratio occurs repeatedly. The side of the pentagon is in the golden ratio to its diagonals . The diagonals are again divided in a golden ratio, i.e. H. AD is to BD as BD is to CD . The proof uses the similarity of chosen triangles .

Construction with compass and ruler for a given circumference

Construction of a pentagon in an enclosing circle

For the regular pentagon there is a mathematically exact construction for determining the side length (see illustration).

1. Draw a circle (later perimeter , blue) with radius r around the center point M.
2. Draw in two diameters that are perpendicular to each other (red).
3. Halve a radius (magenta, point D).
4. Draw a circle (green) with the radius DE around point D. It intersects the straight line AM at point F. The segment EF is the length of the side.
5. To remove the area, draw another arc (orange) with radius EF around E. He cuts the first circle (blue) in G. Repeat the process accordingly.

Calculation for construction:

${\displaystyle {\overline {EM}}=r\cdot 1}$

${\displaystyle {\overline {DM}}=r\cdot {\frac {1}{2}}}$

${\displaystyle {\overline {DE}}=r\cdot {\sqrt {1+\left({\frac {1}{2}}\right)^{2}}}=r\cdot {\frac {\sqrt {5}}{2}}}$

${\displaystyle {\overline {MF}}=r\cdot \left({\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=r\cdot {\frac {{\sqrt {5}}-1}{2}}}$

${\displaystyle {\overline {EF}}=r\cdot {\sqrt {1+\left({\frac {{\sqrt {5}}-1}{2}}\right)^{2}}}}$

Reshaping the factor:

${\displaystyle {\frac {\overline {EF}}{r}}={\sqrt {1+{\frac {5-2\cdot {\sqrt {5}}+1}{4}}}}={\sqrt {{\frac {4}{4}}+{\frac {5-2\cdot {\sqrt {5}}+1}{4}}}}}$

${\displaystyle {\frac {\overline {EF}}{r}}={\sqrt {\frac {4+5-2\cdot {\sqrt {5}}+1}{4}}}={\sqrt {\frac {10-2\cdot {\sqrt {5}}}{4}}}}$

${\displaystyle {\frac {\overline {EF}}{r}}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}}$

This corresponds exactly to the factor in the formula above for the side length .

The sides of the triangle MFE ( not shown) correspond exactly to the side lengths of the regular hexagon ( ME ), the regular pentagon ( EF ) and the regular decagon ( FM ) with the given circumferential radius r.

Construction with compass and ruler with a given side length

With application of the golden ratio , external division

Pentagon with a given side length

1. Draw a segment AB , the length of which is the given side of the pentagon.
2. Extend the distance from point A by about three quarters of the distance AB .
3. Draw an arc around point B with radius AB .
4. Draw an arc around point A with radius AB , the result is the intersection point F.
5. Drop a perpendicular from point F to segment AB with base point G.
6. Draw a parallel to the line FG from point A to over the circular arc around point A, the point of intersection H results.
7. Draw an arc around the point G with the radius GH up to the extension of the segment AB , the intersection point J.
8. Draw an arc around point B with radius BJ up to the vertical that goes through point F, the points of intersection D on the vertical and E with the arc around point A.
9. Draw an arc around point D with radius BA until it intersects the arc around point B, resulting in intersection point C.
10. Connect the points BCDEA, this results in the regular pentagon.

Conclusion

As in the construction with a given circumference , the golden ratio is the decisive element here too .

To compare the construction variants, the point designations are supplemented with indices: u for the construction with a given circumference, s for the construction with a given side length.

1. Side of the pentagon:
   ${\displaystyle {\overline {E_{u}F_{u}}}\;{\widehat {=}}\;{\overline {A_{s}B_{s}}}}$
2. Radius for the golden ratio:
   ${\displaystyle {\overline {D_{u}E_{u}}}\;{\widehat {=}}\;{\overline {G_{s}H_{s}}}}$
3. Route conditions of the golden section:
   ${\displaystyle \Phi ={\frac {\overline {A_{u}F_{u}}}{\overline {A_{u}M_{u}}}}={\frac {\overline {A_{u}M_{u}}}{\overline {M_{u}F_{u}}}}\;\;\;=\;\;\;{\frac {\overline {B_{s}J_{s}}}{\overline {A_{s}B_{s}}}}={\frac {\overline {A_{s}B_{s}}}{\overline {A_{s}J_{s}}}}\;\;\;=\;\;\;{\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618}$

Polyhedron with regular pentagons

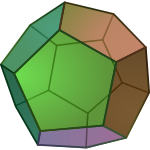
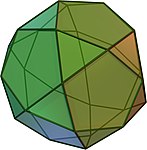
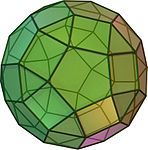
The dodecahedron is the only Platonic solid that has regular pentagons as side faces . Some Archimedean solids also contain regular pentagons, namely the icosidodecahedron , the truncated icosahedron , the rhombicosidodecahedron, and the beveled dodecahedron .

• 

  Dodecahedron

• 

  Icosidodecahedron

• 

  Truncated icosahedron (football body)

• 

  Rhombicosidodecahedron

• 

  Beveled dodecahedron

Paper folding

By pulling together an overhand knot made from a strip of paper , it takes on the shape of a regular pentagon.

Knotted strip of paper

Parquet with pentagons

→ Main article : Parquet with pentagons

The 15 types of level tiling with congruent , convex pentagons

There are only 15 different pentagons with which a surface can be tiled without gaps if only one type of tile is used. The French mathematician Michaël Rao did not provide proof of this until 2017.

Occurrence

nature

Okra fruits

Sliced ​​star fruit

The okra as well as the star fruit have the shape of a pentagon in cross section. The morning glory flowers are also pentagonal. Also starfish and brittle stars have a five-pointed symmetry. Many cyclic compounds contain a five-membered ring structure (such as cyclopentane , γ-butyrolactone , furan , furanoses, etc.).

Architecture and fortress construction

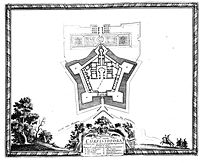
The floor plan of a modern bastion fortress often has the shape of a pentagon. Regular pentagons are the completely rebuilt fortress Bourtange in the Netherlands and Nyenschanz (today in St. Petersburg ), the citadel of Jaca , the citadel of Pamplona , the fortress Dömitz , the citadel of Turin , the citadel of 's-Hertogenbosch , the citadel of Strasbourg , the citadel of Amiens , the citadel of Vitry-le-François by Girolamo Marini , which was demolished in 1598 , the citadel of Antwerp , the citadel of Doullens (Picardy, only in parts on a regular floor plan), the citadel of Lille , the Harburg Castle , the Citadel Vechta , the Citadel of Munster , the Fort Nieuw-Amsterdam , the Fort of Copenhagen , Tilbury Fort in Essex east of London , the high fortress Wülzburg near Weissenburg in Bavaria and the fortress Goryōkaku in Japan.

The type of fortified palace (Palazzo in fortezza) with a regular pentagonal floor plan is embodied in the Villa Farnese , the castles Krzyżtopór and Nowy Wiśnicz and the fortifications of the Łańcut Castle in Poland. The city of Sathmar in present-day Romania had a pentagonal fortress.

The headquarters of the United States Department of Defense in Washington, DC is called the Pentagon because of its regular pentagon shape .

Church buildings such as the Corvinus Church in Hanover, the Dietrich Bonhoeffer Church (Cologne-Lindenthal) , the Zelená Hora pilgrimage church in the Czech Republic or the Church of St. Michael in Detmold (Westphalia) are based on a pentagon .

Tower structures such as the steel traffic tower on Potsdamer Platz or the wooden observation tower on Hohenmirsberger Platte are erected on a pentagonal cross-section .

The pentagonal stone is a boundary stone in Lower Austria.

See also : pentagonal tower

• 

  Citadel of Lille

• 

  Floor plan of the Palazzo Farnese in Caprarola

• 

  Krzyżtopór Castle

• 

  Satellite image of the Pentagon

• 

  Goryōkaku

See also

Pentagon according to the Mascheroni theorem, created solely with a pair of compasses

Web links

Commons : Pentagon  - collection of images, videos and audio files

Wiktionary: Pentagon  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Pentagon  - learning and teaching materials

Individual evidence

1. ^ M. Rao: Exhaustive search of convex pentagons which tile the plane . August 1, 2017, arxiv : 1708.00274
2. ^ Matthias Schütte, Christoph Drösser: Tile Puzzle. In: Die Zeit , No. 32/2017, p. 36.