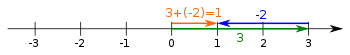Construction with compass and ruler

In Euclidean geometry , a construction with compass and ruler is understood to mean the development of the exact graphic representation of a figure on the basis of given sizes, whereby as a rule only compasses and rulers may be used. The ruler has no marks; you can only draw straight lines with it, but not measure distances.
In geometry , compasses and rulers are also known as Euclidean tools . Solutions to problems that resort to other aids were considered unsatisfactory by the Greeks of the classical period (and later by most geometry practitioners up to the 20th century).
Euclidean tools
The restriction to the "Euclidean tools" was derived from the postulates that Euclid had put together at the beginning of his textbook The Elements . As a result, the only approved uses for these tools are:
- the drawing of a straight line of unlimited length through two arbitrarily given, different points ,
- drawing a circle with a given point as its center and passing through any other given point, and
- transferring or cutting off a route on a straight line or a circular line.
An example would be the construction of a triangle from three specifications, say two sides and an angle .
history
In ancient times, collapsing compasses were called for , i.e. those that snap shut when lifted from a sheet of paper. Later, the non-collapsing compass was also allowed for constructions - not least because the same points can be constructed with a ruler and a collapsing compass as with a ruler and a non-collapsing compass.
The construction using only compasses and (unscaled) ruler was for many centuries the crown of mathematical logic. For a long time, however, it was considered largely exhausted. The discovery of a construction method for the regular seventeenth on March 30, 1796 by Carl Friedrich Gauß was the first major innovation in two thousand years. With the help of the Galois theory about zeros of polynomials , which was developed in the 19th century, statements could also be made about constructible polygons and the trisection of arbitrary angles .
Many mathematicians have tried for years - as we now know unsolvable - tasks such as squaring the circle . However, within the last 100 years or more, the Euclidean limitation has been seen more and more as an unnecessary limitation of possibilities. Some critics even saw it as a so-called mental block. The range of tools has therefore been expanded. A general division of the angle can be done with the help of a template, the edge of which forms an Archimedean spiral . In the second half of the 19th century, the " Tomahawk " was a device for the general three-way division of the angle.
According to the Mohr-Mascheroni theorem (after Georg Mohr and Lorenzo Mascheroni ), construction tasks with compasses and ruler can also be carried out with the compass alone and according to the Poncelet-Steiner theorem (after Jean-Victor Poncelet , Jakob Steiner ) also with the ruler and a given circle.
Algebraic Operations
With a pair of compasses and ruler you can carry out the following elementary algebraic operations with graphically given or already constructed real numbers (that is, construct the result in the representation on the number line ):
- the addition of two numbers (construction of a sum),
- the subtraction of two numbers (construction of a difference),
- the multiplication of two numbers (construction of a product),
- the division of a number by a number other than zero (construction of a quotient),
- the taking of the square root of a non-negative number (construction of a square root).
- the square of a segment or a number (construction of a square)
All numbers that can not be obtained by applying a finite number of these elementary operations can not be constructed with compasses and ruler either. There are even uncountably many, namely (if the numbers 0 and 1 are given) all transcendent numbers such as the circular number or Euler's number , but also every algebraic number whose degree is not a power of two , such as the number of degree 3 as a zero of the irreducible polynomial .
For the construction of the product and the reciprocal value , the ray theorem is used and for the construction of square roots the cathetus set or the height theorem of Euclid (see drawings below).
The Euclidean planes (in the sense of synthetic geometry ) over Euclidean solids form a geometric structure that was specially developed to represent the possibilities of the constructions with compasses and rulers algebraically .
Intermediate steps, for example to construct the square in the picture , have been left out for the sake of clarity.
Construction of the root from a product
by adding the factors (6 + 4) and using the theorem of heights or the geometric meanConstruction of the root from a product, by subtracting the factors (6 - 4) and with the help of the catheter set
Construct a decimal number using the third theorem of rays
Impossible constructions
Many geometric figures cannot be constructed exactly with compasses and ruler alone. Among them are the classic problems of ancient mathematics :
- the trisection of the angle ,
- the doubling of the cube ,
- the squaring of the circle
such as
- the conic sections (with the exception of the circle ) and
- many regular polygons .
The proof that these problems basically not with compass and straightedge to be resolved, but it was not until the 19th century. Yet attempts to accomplish the impossible resulted in a range of accomplishments. The Greeks found some solutions to the "classical" problems with other tools, discovering many results from higher geometry.
Approximation construction
For some figures that cannot be constructed with compasses and rulers or for which the construction is too complex, there are possibilities to construct them at least approximately. These approximation constructions come very close to the real object. Well-known approximation constructions are, for example, the approximation construction for the circle number Pi by Kochański , the approximation construction for the squaring of the circle , the approximation construction for the regular heptagon and the approximation construction for the regular nine corner .
application
The basic geometric constructions play an essential role , especially in the representational geometry and in technical drawing . It starts with school mathematics and has a wide range of applications in the technical draftsman's profession.
literature
- Ludwig Bieberbach : Theory of Geometric Constructions . Birkhäuser, Basel, 1952
- Hans-Wolfgang Henn: Elementary Geometry and Algebra: Basic Knowledge for Studies and Mathematics Lessons . Vieweg, 2003, pp. 31-60
- George E. Martin: Geometric Constructions . Springer, 2012, ISBN 978-1-461-20629-3
- Nicholas D. Kazarinoff: Ruler and the Round: Classic Problems in Geometric Constructions . Courier Dover (new edition), 2012, ISBN 978-0-486-14361-3
Web links
- Compasses and ruler: A free program for constructions on the computer
- Constructions with compasses and ruler (with instructions) (at mathezentrale.de)
Individual evidence
- ^ Felix Klein: Gauß 'scientific diary 1796-1814. With notes. (For this 1 facsimile). In: Mathematical Annals . tape 57 , 1903, ISSN 0025-5831 , p. 1–34 ( digizeitschriften.de [accessed April 1, 2019]).
- ^ Carl Friedrich Gauß: Disquisitiones arithmeticae . Humboldt University of Berlin, January 1, 1801 ( hu-berlin.de [accessed March 31, 2019]).



![{\ sqrt [{3}] {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)