Squaring the circle

The title of this article is ambiguous. Further meanings are listed under squaring the circle (disambiguation) .

The square and the circle have the same area.

The squaring of the circle is a classic problem of geometry . The task is to construct a square with the same area from a given circle in finitely many steps . It is equivalent to the so-called rectification of the circle , i.e. the construction of a straight line that corresponds to the circumference of the circle . This in turn corresponds to the construction of the number of circles (half the circumference) from the segment, the length of which is equal to the unit of  length . If the means of construction are limited to rulers and compasses , the task is unsolvable due to the transcendence of . Only in 1882 could this be proven by the German mathematician Ferdinand von Lindemann . ${\displaystyle \pi }$ ${\displaystyle 1}$ ${\displaystyle \pi }$

Squaring the circle is one of the most popular problems in mathematics. For centuries, both mathematicians and laypeople searched in vain for a solution. The term squaring the circle has become a metaphor for an impossible task in many languages .

history

prehistory

Approximation method used by Ahmes in the Rhind papyrus :
A circle with a diameter of 9 in a square with side length 9, which is divided into nine smaller squares with side length 3.
The area of ​​the circle corresponds roughly to that of an (irregular) octagon (7 × 9) and more precisely that of a square with side length 8 (64).

There were already methods for calculating circular areas in the ancient oriental civilizations . For example, in the Rhind papyrus (around 1650 BC) the diameter of the circle is divided into 9 parts. Its exact area in these units is . This value is then approximated by a square of edge length 8, i.e. by . In a second method, the circle is approximated by an irregular octagon . For this purpose, equal triangles with a total of 18 units of area are cut off from the 9 × 9 square in which it is inscribed, so that 63 remain. Such sample solutions were obtained from practice and intended for practice, there were no further theoretical considerations, in particular no distinction was made between exact solution and approximation. ${\displaystyle {\tfrac {\pi }{4}}\cdot 9^{2}=63{,}62\ldots }$ ${\displaystyle 8^{2}=64}$

A deductive approach in mathematics , in which evidence- based propositions replace sample problems, developed from the 6th century BC onwards. In Greece. To some extent it can already be seen in Thales of Miletus , more clearly in the school of the Pythagoreans founded by Pythagoras of Samos . With the discovery of incommensurable stretches in the late 6th or early 5th century BC, commonly attributed to the Pythagorean Hippasus of Metapont , It turned out that there are constructible objects (for example the diagonal of a square) that cannot be represented as an integer ratio. This seemed remarkable since the only known types of numbers were integers and integer ratios (in today's parlance the "rational numbers"). Any geometric lines had to be commensurable, i.e. they had to have an integer length ratio to one another. As a result of the discovery, lengths could now be constructed geometrically, which could not be represented arithmetically as a “number” in the previous sense (in today's parlance it is a matter of “irrational numbers”). The geometry could suddenly represent more than the arithmetic could. As a result of this discovery, arithmetic took a back seat in favor of geometry, equations now had to be solved geometrically, for example by placing figures next to one another and converting different figures into rectangles or squares. The three classical construction problems of ancient mathematics date from the late 5th century, besides squaring the circle, the task of dividing the angle into three and the Delic problem of doubling the cube.

A restriction of the construction materials to compasses and rulers was not generally required. While dealing with the classic problems, solutions based on advanced tools were found early on. In the course of time, however, an attitude emerged that required the greatest possible restriction. At the latest with Pappos this extensive restriction had become a measure.

Early work

According to the Greek writer Plutarch , the philosopher Anaxagoras was one of the first to have "written down the square of the circle in prison (or: drawn, ancient Greek ἔγραφε )", Plutarch does not provide any further details about Anaxagoras' construction. Anaxagoras would stay in prison for about 430 BC. When the philosopher was accused of ungodliness in Athens .

More detailed sources on the beginnings of research are mainly comments on the works of Aristotle from late antiquity , i.e. writings that were written about 900 years apart. The chronological order and exact thought processes of the first approaches are accordingly uncertain. The most important works of the 5th century BC BC come from Hippocrates of Chios , Antiphon , Bryson of Herakleia and Hippias of Elis .

The "little moon of Hippocrates": The area of ​​the gray "little moon" corresponds to that of the right-angled triangle ABC.

The conversion of triangles into rectangles, of rectangles into squares ( squaring the rectangle ) or the addition of two squares ( Pythagorean theorem ) could already be managed with the well-known geometrical theorems. Hippocrates of Chios could around 440 BC. Give an example of a curvilinearly limited area that could be converted exactly into a square. Based on the axiom still used by him that the areas of similar segments of a circle behave like the squares over their chords, Hippocrates succeeded in squaring areas delimited by circular arcs, the so-called " little moon of Hippocrates ". However, the squaring of the circle cannot be achieved in this way, since only certain moons - for example those above the side of the square, but not those above the side of a regular hexagon - can be squared.

The fact that triangles (and thus any polygons) could be converted into a square was a second approach to construct a polygon with the same area as the circle. Antiphon had the idea of ​​approximating the circle with inscribed polygons. Bryson of Herakleia refined this procedure by additionally approximating the circle with circumscribed polygons and forming an intermediate value.

Hippias von Elis developed around 425 BC Chr. To solve the angular trisection, a curve that was created mechanically by superimposing a circular with a linear movement. A good hundred years later, Deinostratos discovered that with the help of this curve, the so-called quadratrix , the line of length - and thus a square with the area - can be constructed with the help of other elementary constructions . However, since the quadratrix itself is a so-called transcendent curve (see proof of impossibility ), i.e. it cannot be generated with a compass and ruler, the solution in the strict sense was not achieved. ${\displaystyle 2/\pi }$ ${\displaystyle \pi }$

Archimedes

Circle quadrature with the help of the spiral: A denotes the point of the spiral around the origin O, which it reaches after the first revolution. The tangent to the spiral at this point intersects the perpendicular to OA in B. According to Archimedes, the segment BO is equal to the circumference of the circle with radius OA, the area of ​​the red circle therefore equal to the area of ​​the blue triangle.

A detailed treatise with the title Circular Measurement has come down to us from Archimedes . Archimedes proved three basic theorems in this work:

1. The area of ​​a circle is equal to the area of ​​a right triangle with the circle radius as the one and the circumference as the other leg . The area of ​​the circle can therefore be calculated as ½ · radius · circumference.
2. The area of a circle is related to the square of its diameter almost as ¹¹ / ₁₄ .
3. The circumference of a circle is greater than 3+ ¹⁰ / ₇₁ and smaller than 3 + ¹⁰ / ₇₀ of the diameter.

With the first sentence, the problem of squaring the circle was reduced to the question of the constructability of the circumference of a circle from the given radius and thus the constructability of . In the third set Archimedes was equal to an easy as well as accurate approximation of this number, namely ²² / ₇ , a value (≈ 3.143), which is for practical purposes still use. The second movement is a simple corollary from the other two; that the area of ​​a circle is proportional to the square of its diameter, and was already known to Euclid . Archimedes gave here the value of the proportionality constant. ${\displaystyle \pi }$

As proof of his statements, Archimedes used the idea of ​​Bryson of Herakleia, with which one can achieve any approximation of the circle by inscribed and circumscribed regular polygons . Starting from the inscribed hexagon and circumscribed triangle, Archimedes arrived at the 96-sided by successively doubling the number of pages. A clever estimate of the square roots occurring in the individual calculation steps resulted in the limits mentioned in sentence 3.

In another work on spirals , Archimedes described the construction of the Archimedean spiral , later named after him , which, like Hippias' Quadratrix, is obtained by superimposing a circular with a linear movement. He showed that by applying the tangent to this spiral, the circumference of a circle can be removed on a straight line. Later commentators point to the preparatory work done in this way to square the circle, Archimedes himself made no statement. As with the Quadratrix, however, neither its spiral itself nor its tangent can be constructed with a compass and ruler.

middle Ages

The quadrature of the circle by Franco von Liège: Franco divides the circle into 44 sectors, which he puts together to form a rectangle.

As a result of an increased interest in ancient mathematics in Christian Europe from around the 11th century onwards, a number of treatises on the squaring of the circle emerged, but without making any significant contributions to the actual solution. Is to be regarded as a step backwards that in the Middle Ages of Archimedes' Approximation of ²² / ₇ for the circle constant long considered exactly was.

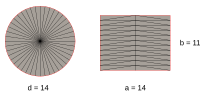
One of the first authors of the Middle Ages to revisit the problem of circular quadrature was Franco von Liège . His work De quadratura circuli was written around 1050 . Franco first presents three squares, which he rejects. The first two options for the side length of the square ⁷ / ₈ or for the diagonal ¹⁰ / ₈ to the circle diameter which relatively poor approximations of 3 ¹ / ₁₆ and 3 ¹ / ₈ for equivalent. The third suggestion, in turn, equates the circumference of the square with the circumference of the circle, thus requiring the latter to be rectified. ${\displaystyle \pi }$

Franco's own solution is based on a circle with a diameter of 14. The area of which he sits exactly as 7² × ²² / ₇  on = 154th After Franco's reasoning can be calculated not face the same square find as the square root of ²² / ₇ is irrational, as geometrically constructible incommensurable distance (see history but the square root) delivers ²² / ₇ squaring. To do this, he divides the circle into 44 equal sectors , which he combines to form a rectangle of side lengths 11 and 14. However, Franco does not explain the necessary trick in which he replaces the circular sectors with right-angled triangles with cathets of length 1 and 7. Another problem is his unsuccessful attempt to then convert the rectangle into a square by means of a suitable decomposition. Obviously Franco was not familiar with the traditional Greek process.

Later treatises on scholasticism are more or less exhausted in weighing up the arguments of the well-known classics. Only with the dissemination of Latin translations of Archimedes' writings in the late Middle Ages, the value was ²² / ₇ recognized as an approximation and search for new solutions to the problem, such as by Nicholas of Cusa . He took up the idea of ​​approximating the circle by a series of regular polygons with an increasing number of sides, but in contrast to Archimedes did not seek to determine the circumference, but rather the circle radius with a given constant circumference of the polygons. In a letter to the doctor and naturalist Paolo Toscanelli , von Kues gave such a solution, which he thought was accurate. The value determined from this for the circle number is at least between the limits given by Archimedes. The actual work of Kues on the topic provides significantly poorer approximations and thus became the target of a polemic by Regiomontanus , who proved the inaccuracy of the calculations and described the evidence as "philosophical, but not mathematical".

Advances in circular measurement in the early modern period

From the 16th century onwards, the further development of the Archimedean approximation method and the emergence of modern analytical methods brought advances in circle computation.

In the original Archimedes method, the circumference of a circle is estimated by the circumference of a polygon inscribed in the circle and that of a polygon encircled by the circle. More precise limits result from an increase in the number of corners. The Dutch mathematician Willebrord van Roijen Snell (Snellius) found that, without increasing the number of pages, finer bounds for the length of an arc than just the chords of the polygons can be specified. However, he could not strictly prove this result . Christiaan Huygens worked out and improved the Snellian approach in his work De circuli magnitudine inventa , in which he also proved the theorems established by Snellius. Using a purely elementary geometric method , Huygens succeeded in delimiting the area between the polygon and the circle so well that, with the corresponding number of sides of the polygons, he received the number of circles to at least four times as many decimal places as Archimedes' method.

The purely geometric approach to determining the circular constant was essentially exhausted with Huygens' work. Better approximations were obtained with the help of infinite series , especially the series expansion of trigonometric functions . Although François Viète had already found the first exact representation of through an infinite product at the end of the 16th century by considering certain route conditions of successive polygons , this formula proved to be unwieldy. A simpler series that also only needs multiplications and divisions comes from John Wallis , another representation of the circle number as a continued fraction from William Brouncker . The series for the arctangent found by James Gregory and independently of Gottfried Wilhelm Leibniz was more important in practice . Although this series itself only converges slowly , other series can be derived from it, which in turn are very suitable for calculating the number of circles. At the beginning of the 18th century more than 100 digits of were calculated with the help of such series , but new knowledge about the problem of circular quadrature could not be gained. ${\displaystyle \pi }$ ${\displaystyle \pi }$

Algebraic problem and irrationality of ${\displaystyle \pi }$

At the beginning of his Géométrie Descartes describes the new approach of analytic geometry.

Oronce Fine , Quadratura circuli , 1544.

JP de Fauré , dissertation, découverte, et demonstrations de la quadrature mathematique du cercle , 1747.

In order to solve the problem, it was necessary, on the one hand, to give the geometric term “constructible” an algebraic meaning and, on the other, to have a closer look at the properties of the circle number.

A geometric construction with compasses and ruler is based on a finite number of given points and determines new points in a finite number of steps by intersecting two straight lines, two circles or a straight line with a circle. The translation of this procedure into the language of algebra was achieved through the introduction of coordinate systems within the framework of the analytical geometry developed mainly by Pierre de Fermat and René Descartes in the 17th century . With the new means, straight lines and circles could be described by equations, intersections could be determined by solving systems of equations. It turned out that the line lengths that can be constructed with compasses and ruler starting from a line of length 1 correspond exactly to the numbers that result from a finite number of rational (basic) operations (addition, subtraction, multiplication and division) and a finite number Derive the number of square roots resulting from the reverse operation of squaring the number 1. In particular, these lengths correspond to algebraic numbers , that is, a subset of the numbers that are a solution of an algebraic equation of any degree with rational coefficients . Numbers that are not algebraic are called transcendent . Accordingly, starting from length 1, transcendent lengths cannot be constructed in finitely many steps with a compass and ruler.

The starting point for further investigations of the circle number were some fundamental findings from Leonhard Euler , which he had published in 1748 in his work Introductio in analysin infinitorum . Among other things, Euler used the Euler formula named after him

${\displaystyle e^{i\,z}=\cos z+i\sin z}$

for the first time a connection between trigonometric functions and the exponential function and also provided some continued fraction and series representations of and the Euler number e later named after him . ${\displaystyle \pi }$

Johann Heinrich Lambert took advantage of this preliminary work, who was able to show for the first time with the help of one of Euler's continued fraction developments in 1766 that e and irrational numbers, i.e. numbers that cannot be represented by an integer fraction. A small gap in Lambert's argument was closed in 1806 by Adrien-Marie Legendre , who also provided the proof of irrationality for . ${\displaystyle \pi }$ ${\displaystyle \pi ^{2}}$

The suggestion that it could not be algebraic was at least voiced by Euler, Lambert, and Legendre. However, until the middle of the 19th century it was not yet clear that there had to be transcendent numbers at all. Joseph Liouville succeeded in proving this in 1844/1851 through the explicit construction of transcendent Liouville numbers . ${\displaystyle \pi }$

Proof of impossibility

Ferdinand von Lindemann was finally able to prove in 1882 that is not algebraic, but transcendent . Therefore it is not possible to construct a straight line and it is impossible to square the circle. ${\displaystyle \pi }$ ${\displaystyle \pi }$

Lindemann drew on a result of the French mathematician Charles Hermite in his work . In 1873 he had shown that Euler's number e is transcendent. Building on this, Lindemann was able to prove the so-called Lindemann-Weierstrass theorem, which states that for any algebraic numbers that are different from one another and for any algebraic numbers the equation ${\displaystyle z_{1},\dots ,z_{r}}$ ${\displaystyle n_{1},\dots ,n_{r}}$

${\displaystyle \sum _{i=1}^{r}n_{i}e^{z_{i}}=0}$

can only apply if all have the value zero. In particular, the expression cannot yield a rational number for any algebraic number z other than zero . After this preparation, Lindemann was able to contradict the assumption that it was algebraic with the help of Euler's identity ; thus had to be transcendent. ${\displaystyle n_{i}}$ ${\displaystyle e^{z}}$ ${\displaystyle \pi }$ ${\displaystyle e^{i\pi }=-1}$ ${\displaystyle \pi }$

Lindemann's proof of the transcendence of was considerably simplified in the following years and decades, for example by David Hilbert in 1893. ${\displaystyle \pi }$

Popularity of circular quadrature

Like few other questions, the squaring of the circle also achieved great popularity outside of mathematics. As a result, many mathematical laypeople tried to solve the seemingly simple problem; some believed they had found them.

Reports of a growing volume of amateur work from the 18th and 19th centuries and examples on the subject can be found in Jean-Étienne Montucla , Johann Heinrich Lambert and Augustus de Morgan . As a rule, these were processes in which the problem was solved "exactly" mechanically, numerically or by means of a geometric approximation construction. Such work was brought to such a large number of mathematicians or scientific institutions that, for example, the Paris Academy of Sciences in 1775 felt compelled to officially refuse further investigation of alleged solutions to the quadrature of the circle:

L'Académie a pris, cette année, la résolution de ne plus examiner aucune solution desproblemèmes de la duplication du cube, de la trisection de l'angle ou de la quadrature du cercle, ni aucune machine annoncée comme un mouvement perpétuel .

“ This year, the academy made the decision not to investigate the solutions to the mathematical problems relating to doubling the cube, dividing the angle into three and squaring the circle, nor any machine that claims to be a ' perpetual motion machine '. "

Even after Lindemann's proof of impossibility in 1882, supposed circular quadratures were published in the 20th century, which in more recent times have become the subject of entertainment mathematics as unsuccessful attempts by amateur mathematicians .

One of the main reasons for its high attractiveness, especially for mathematical laypeople, is probably the very elementary problem that can be understood or at least seems to be understandable even without in-depth mathematical knowledge. Together with the numerous unsuccessful attempts at finding a solution by established scientists, the quadrature of the circle acquired a veritable nimbus .

Another reason, not to be underestimated, for the numerous efforts to square the circle was the widespread opinion that the solution to the problem would come at a high price - a misconception that possibly goes back to the erroneous assumption that the circle quadrature was directly connected with the long unsolved problem of the exact determination of the geographical longitude at sea, on the solution of which prices were indeed exposed. The saga of the competition persisted so persistently that even in 1891 Meyers Konversations-Lexikon could still read that " Charles V had offered 100,000 thalers and the Dutch States General an even higher sum".

Prominent circle squarers

A prominent example of an amateur mathematician who believed he had found the square of the circle was the English philosopher Thomas Hobbes . His solution published in his work De corpore in 1665 - in reality an approximation construction - was refuted by John Wallis that same year. In the period that followed, a sharp argument developed between the two, which did not end until Hobbes' death in 1679.

Lambert reports three quadratures of the circle by means of a certain rational value. The appeared in the mid-18th century works are based on the approximation ³⁵ / ₃₁ for the ratio of diameter to the side of the equal area square. This gives the approximation for the number of circles

${\displaystyle \pi \approx {\frac {3844}{1225}}=3{,}1{\color {red}37\;9\;\ldots }\;.}$

One of the three authors, the preacher Merkel from Ravensburg , devoted Gotthold Ephraim Lessing 's poem "On the Lord M ** the inventor of the squaring of the circle".

The circular quadrature by the American doctor Edward J. Goodwin even appeared in the first volume of the American Mathematical Monthly in 1894 , if only as an advertisement from the author. The work itself is contradicting itself and, depending on the reading, allows several values ​​for . It formed the basis for a 1897 Parliament of Indiana submitted bill, called the Indiana Pi Bill , the findings Goodwin should be made into law by the. ${\displaystyle \pi }$

Arts and Culture

As the earliest evidence of the appearance of a so-called “circle square” or “quadrator”, a passage in Aristophanes ' comedy The Birds from the 5th century BC is occasionally cited, in which Meton appears as a surveyor and the floor plan of a new city with geometric aids wants to define that “the circle becomes a square”. What is meant by this is not the squaring of a circle, but the creation of two streets that meet at right angles, even if the expression appears to be an allusion to the quadrature of the circle.

In 1321, Dante Alighieri, in his Divine Comedy , portrayed squaring the circle as a task beyond human comprehension and compared to his own inability to understand Paradise:

“As
if to measure yourself in vain The mathematician struggles with thinking,
Because he lacks the principle he needs:   135

That's how I felt at this new sight.
I wanted to see how the picture
related to the circle and where it would find its place;

But my wings were not enough here,
if my mind had not been struck by lightning,
which contemplated the fulfillment of my wish. "

- Dante Alighieri, Ludwig Gottfried Blanc (translator) : The Divine Comedy - Paradise - Singing 33, lines 133 to 141

In James Joyce's seminal novel Ulysses from 1922, the main character is Leopold Bloom , an advertisement acquirer . In the summer of 1882 he worked hard to solve the problem of squaring the circle in order to obtain a supposedly large fortune. Towards the end of the novel, in a long dialogue with his father, Rudolf Virág, he had to sadly and disappointed admit that he had failed.

“VIRAG […] You intended to devote a full year to studying the problem of religion and the summer months of 1882 to squaring the circle and winning that million. Pomegranate! There is only one step from the sublime to the ridiculous. Pajamas, could we say? [...]

BLOOM I wish it was the end now. Night suit was never. Hence this one. But tomorrow is a new day, will be. Was past is today. What is now will be tomorrow as it was now, yesterday's past. "

- James Joyce : Ulysses: Novel

Approximate constructions

Babylonian method according to Dürer (1525).

Although an exact solution with a compass and ruler is not possible, there are approximate constructions for circular quadrature that are precise enough for many purposes. Simple methods, already known in antiquity, give an integer ratio of the diameter or radius of the circle to the side or diagonals of the square. In addition to the equation of the circle of diameter 9 with the square of side length 8, mentioned in the Rhind papyrus, that of the circle of diameter 8 with the square of the diagonal 10 was also known. This construction can be found on the one hand in the Babylonians and on the other hand in the publications of the Roman surveyor Vitruvius . It returns the value 3 ¹ / ₈ for . In order to provide a convenient drawing method, Albrecht Dürer took up this construction again in 1525 in his work Vnderweysung der messung mit dem zirckel und richtscheyt . Dürer is aware that this is a purely approximate solution; he explicitly writes that an exact solution has not yet been found: ${\displaystyle \pi }$

“It would be necessary to know Quadratura circuli , that is the equality of a circle and a square, so that one has as much content as the other. But this has not yet been demonstrated by scholars. Mechanice, that is incidental, that is, that it is not missing in the work or is only missing a little, so this equality may be made. Tear a crossing and divide the local line into ten parts and then tear a circular diagram, the diameter of which should be eight parts, like the quadrature of ten; how I tore that open below. "

- Albrecht Dürer : Vnderweysung the measurement with the zirckel and richtscheyt

Construction by Kochański

→ Main article : Kochański's approximate construction

Approximate construction by Kochański (1685).

The Polish mathematician Adam Adamandy Kochański discovered a classic approximate solution for half the circumference of the circle in 1685. It only needs one circular opening. The actual construction consists of a rectification of the semicircle. From the given radius, Kochanski constructed an approximately straight line of length d. H. approximately half the circumference of the circle The rectangle drawn in red in the adjacent drawing therefore has almost the same area as the circle. The approximate quadrature follows from this elementary with the help of mathematical laws of the right triangle , described in the quadrature of the rectangle . Kochański approximates the number of circles to four decimal places: ${\displaystyle r}$ ${\displaystyle r\cdot \pi ,}$ ${\displaystyle {\tfrac {U}{2}}.}$ ${\displaystyle {\overline {AZ}}\cdot r=r\;\cdot \approx \pi \cdot r}$

${\displaystyle \pi =3{,}141\;592\ldots \approx {\overline {AZ}}=r\cdot {\sqrt {(3-\tan 30^{\circ })^{2}+4\,}}\ \approx \ 3{,}141\;5{\color {red}33}\cdot r}$

Examples to illustrate the errors:

For a circle with a radius r = 100 m, the side length error would be ≈ −1.7 mm.

For a circle with the radius r = 1 m, the error in the area A would be ≈ −59 mm ² .

Construction by Jacob de Gelder

Construction by Jacob de Gelder with continuation (dashed lines).

In 1849, an elegant and obviously simple construction by Jacob de Gelder (1765–1848) appeared in Grünert's archive . That was 64 years earlier than ZA Ramanujan's publication of the comparable construction .

It is based on the approximation

${\displaystyle \pi \approx {\frac {355}{113}}=3{,}141\;592{\color {red}\;9\;\ldots }}$

and the division of the value into the two summands

${\displaystyle 3+0{,}141\;592{\color {red}\;9\;\ldots }.}$

The value of this fraction already has six decimal places in common with the circle number . It comes from the Chinese mathematician Zu Chongzhi from the 5th century and is therefore also called the Zu Chongzhi fraction . ${\displaystyle \pi }$

Jacob de Gelder did not construct the side of the square; it was enough for him to find the following value:

${\displaystyle {\overline {AH}}={\frac {4^{2}}{7^{2}+8^{2}}}=0{,}141\;592{\color {red}\;9\;\ldots }}$.

The illustration opposite - described below - shows Jacob de Gelder's construction with continuation.

Draw two perpendicular center lines of a circle of radius CD = 1, and determine the intersection points A and B. Put the distance CE = firmly and connect with E A. Determine on AE and A from the distance AF = . Draw FG parallel to CD and connect E with G. Draw FH parallel to EG , then AH = Determine BJ = CB and then JK = AH . Halve AK in L and draw the Thales circle around L from A, this results in the intersection point M. The segment BM is the root of AK and thus the side length a of the sought-after, almost identical square. ${\displaystyle {\tfrac {7}{8}}}$ ${\displaystyle {\tfrac {1}{2}}}$ ${\displaystyle {\tfrac {4^{2}}{7^{2}+8^{2}}}.}$

Examples to illustrate the errors:

For a circle with the radius r = 100 km, the error of the side length would be a ≈ 7.5 mm

For a circle with the radius r = 1 m, the error of the area A would be ≈ 0.3 mm ²

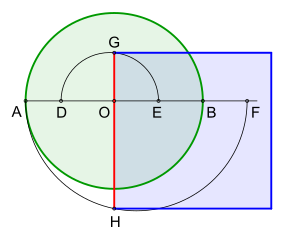
Construction by EW Hobson

Approximate construction according to EW Hobson, with continuation of the construction.

A particularly simple and easily comprehensible construction was made by EW Hobson in 1913. It only requires three semicircles and two mutually perpendicular lines for the side of the square .

The adjacent picture shows the construction with the circle and the square you are looking for.

Specifications and description:

• Circle with diameter ${\displaystyle AOB}$
• ${\displaystyle {\overline {OD}}={\frac {3}{5}}\cdot r,\;{\overline {OF}}={\frac {3}{2}}\cdot r,\;{\overline {OE}}={\frac {1}{2}}\cdot r.}$

Draw the semicircles with and as a diameter. Finally, set up the perpendicular to through the intersection points created thereby and provide the side length of the square you are looking for ${\displaystyle DGE,AHF}$ ${\displaystyle {\overline {DE}}}$ ${\displaystyle {\overline {AF}}}$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle O.}$ ${\displaystyle G}$ ${\displaystyle H}$

${\displaystyle {\overline {GH}}=r\cdot 1{,}772\;4{\color {red}67\ldots }\;[LE].}$

For a circle with a radius, four decimal places on the side of the square are the same as in ${\displaystyle r=1\;[LE]}$ ${\displaystyle {\sqrt {\pi }}=1{,}772\;453}$

Example to illustrate the errors:

For a circle with the radius r = 100 m, the error of the side length would be ≈ 1.4 mm

For a circle with the radius r = 1 m, the error of the area A would be ≈ 46 mm ² .

Constructions by SA Ramanujan

Approximate construction according to SA Ramanujan (1913) with drawn square.

In 1913 a construction by the Indian mathematician Srinivasa Ramanujan appeared , which was also based on approximation

${\displaystyle \pi \approx {\frac {355}{113}}=3{,}141\;592{\color {red}\;9\;\ldots }}$

is based. Ramanujan noted, regarding the accuracy of his method, that with a circular area of ​​140,000 square miles, the constructed side of the square deviated only about an inch from the true value.

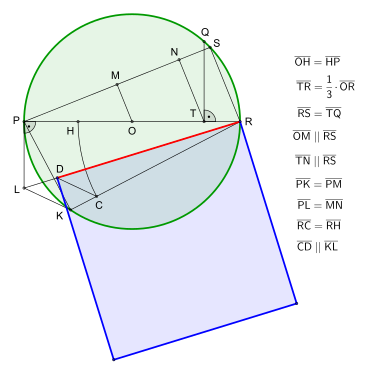
Description (translation):

Let PQR be a circle with the center O, of which PR is the diameter. Halve PO in H, and let T be the point from the tripartite division of OR near R. Draw TQ perpendicular to PR and set the chord RS = TQ.

Connect P with S and draw OM and TN parallel to RS. Set a chord PK = PM and draw the tangent PL = MN. Connect R with L, R with K and K with L. Section RC = RH. Draw CD parallel to KL, [CD] meets RL in D.

Then the square over RD is approximately equal to the circle PQR.

Because ${\displaystyle RS^{2}={\frac {5}{36}}d^{2},}$

where is the diameter of the circle. ${\displaystyle d}$

Consequently ${\displaystyle PS^{2}={\frac {31}{36}}d^{2}.}$

But and are the same or ${\displaystyle PL}$ ${\displaystyle PK}$ ${\displaystyle MN}$ ${\displaystyle PM.}$

Thus and ${\displaystyle PK^{2}={\frac {31}{144}}d^{2},}$ ${\displaystyle PL^{2}={\frac {31}{324}}d^{2}.}$

Consequently ${\displaystyle RK^{2}=PR^{2}-PK^{2}={\frac {113}{144}}d^{2},}$

and ${\displaystyle RL^{2}=PR^{2}+PL^{2}={\frac {355}{324}}d^{2}.}$

But ${\displaystyle {\frac {RK}{RL}}={\frac {RC}{RD}}={\frac {3}{2}}{\sqrt {\frac {113}{355}}},}$

and ${\displaystyle RC={\frac {3}{4}}d.}$

So almost the same. ${\displaystyle RD={\frac {d}{2}}{\sqrt {\frac {355}{113}}}=r{\sqrt {\pi }},}$

Note: If the area of ​​the circle is 140,000 square miles, then RD is about an inch larger than its true length.

Approximate construction according to SA Ramanujan (1914) with continuation of the construction (dashed lines),
see the animation .

In a work from the following year (1914), Ramanujan provided, in addition to other approximation methods, another quadrature with a compass and ruler. This lies the value

${\displaystyle \pi \approx {\sqrt[{4}]{9^{2}+{\frac {19^{2}}{22}}}}=3{,}141\;592\;65{\color {red}2\;\ldots }}$

which comes close to eight digits. In this quadrature, Ramanujan did not construct the side length of the square he was looking for; it was enough for him to show the route OS. In the continuation of the construction on the right, the segment OS is used together with the segment OB to display the mean proportional (red segment OE). ${\displaystyle \pi }$

Description (translation):

Let AB (Fig. 2) be a diameter of a circle whose center is O. Halve the arc ACB in C and third AO in T. Connect B with C and mark off CM and MN as long as AT. Connect A with M and A with N and mark AP on the latter with the same length as AM. Draw PQ parallel to MN, where Q meets AM. Connect O with Q and draw TR parallel to OQ, where R meets AQ. Draw AS perpendicular to AO and the same length as AR, then connect O with S. Then the mean proportional between OS and OB will be very close to one sixth of the circumference, with the error being less than one twelfth of an inch if the diameter is 8000 Miles long.

Continuation of the construction up to the desired side length of the square: Extend AB beyond A and strike the circular arc b ₁ around O with radius OS , this results in S '. Halve BS ' in D and draw the Thales circle b ₂ over D. Draw a straight line from O through C to the Thales circle b ₂ , it intersects b ₂ in E. The segment OE is also called the mean proportional between OS and OB described above geometric mean , it results from Euclid's theorem of heights . Extend the distance EO beyond O and then transfer EO twice more, this results in F and A ₁ and thus the length of the distance EA ₁ with the approximate value of half the circumference described above . Halve the line EA ₁ in G and draw the Thales circle b ₃ over G. Transfer the line OB from A ₁ to the line EA ₁ , it results in H. Create a vertical line on EA ₁ from H to the Thales circle b ₃ , it results B ₁ . Connect A ₁ with B ₁ , so the side length you are looking for is constructed for a nearly equal square A ₁ B ₁ C ₁ D ₁ . ${\displaystyle a}$
${\displaystyle \pi }$ ${\displaystyle a}$

Examples to illustrate the errors:

For a circle with the radius r = 10,000 km, the error of the side length would be a ≈ −2.8 mm

For a circle with the radius r = 10 m, the error would be the area A ≈ −0.2 mm ²

Construction by Louis Loynes

Loynes' construction (1961).

Louis Loynes published a simpler method in 1961. It is based on the finding that the area of ​​the circumference of a right triangle is equal to the square over the larger leg if the tangent of the smaller angle, i.e. the ratio of the smaller to the larger leg,

${\displaystyle {\sqrt {{\frac {4}{\pi }}-1}}=0{,}5227232\dots }$

is, a value very close to the fraction

${\displaystyle {\frac {23}{44}}=0{,}5227272\dots }$

lies. This results in a simple approximation by using the (constructible) right-angled triangle with the cathetus ratio 23:44 to the quadrature. The approximate value for the circle number of

${\displaystyle \pi \approx {\frac {7744}{2465}}=3{,}141\;5{\color {red}82\;\ldots }}$

is a bit better than Kochański's construction.

Examples to illustrate the errors:

For a circle with the radius r = 1 km, the error of the side length would be ≈ −3 mm.

For a circle with the radius r = 1 m, the error of the area A would be ≈ −11 mm ² .

Approximate solution using a constructed fraction

If a fraction is constructed on a ray, the value of which approximately corresponds to the number of circles , using the third ray theorem , it is possible with more or less constructive effort to represent any desired number of decimal places. To determine the side length of the square can, for. B. the break ${\displaystyle \pi }$ ${\displaystyle \pi }$

${\displaystyle {\frac {245850922}{78256779}}=3{,}141\;592\;653\;589\;793{\color {red}\;160\;\ldots }}$

can be used. As an approximation of the number of circles , it provides a remarkable fifteen equal decimal places. The reverse break of this break comes from Johann Heinrich Lambert , who u. on published contributions to the use of mathematics and their application in his book as early as 1770 . ${\displaystyle \pi }$

Non-classical method using square indexes

Squaring the circle with Hippias's quadratrix as an additional aid.

If you loosen the restriction to compasses and rulers and allow further construction means, you get a multitude of possibilities to square the circle or to construct the side length of the square exactly. ${\displaystyle {\sqrt {\pi }}}$

With the help of special transcendent curves, the so-called quadratrices , as the only additional tool, it is possible to exactly square a circle. The existence or availability of such a square matrix is ​​simply assumed in the mathematical model. For practical drawing on paper, it is available, for example, in the form of a template or a plotter print-out , and there are also some special mechanical drawing devices that can be used to generate such curves. The oldest quadratrizes known since antiquity, which are used in circle quadrature, include z. B. the quadratrix of Hippias and the spiral of Archimedes .

The picture on the right shows an example of a quadrature of a circle with the help of the quadrix of Hippias, the graph of which runs through and . ${\displaystyle E,\;{\tfrac {2}{\pi }}}$ ${\displaystyle D}$

After constructing the circle number with Hippias's quadratrix as an additional aid , lengthening the distance according to Thales's theorem results in the root of The drawn square with the side length has exactly the same area as the circle around ${\displaystyle \pi }$ ${\displaystyle {\overline {BH}}}$ ${\displaystyle {\overline {A\pi }}={\overline {AI}}={\sqrt {\pi }}.}$ ${\displaystyle {\sqrt {\pi }}}$ ${\displaystyle A.}$

variants

Tarski's problem of squaring the circle

In 1925, Alfred Tarski set the task of dividing a circle into any number of parts and then moving them through pure movement (i.e. without stretching) so that a square is created.

Miklós Laczkovich came up with the solution in 1989: He proved that it is possible to divide a circle into a finite number of parts and only move them through movement so that a square is created. He cut the circle into 10 ⁵⁰ pieces. For the proof, however, he needs the axiom of choice , which is accepted by most scientists today but cannot be taken for granted. The proof is very similar to the Banach-Tarski paradox .

Laczkovich has proven that (assuming the axiom of choice) such a decomposition exists, but this decomposition cannot be stated explicitly.

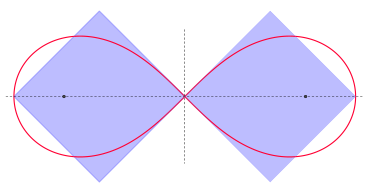
Lemniscates

Squaring the lemniscate.

In contrast to the circle, it is possible to construct two squares for a lemniscate (∞), which span the same area. Their side lengths correspond to the largest lemniscate radius a .

See also

• Quadrature the rectangle
• Squaring the square
• Quadrature the polygon

Literature and Sources

General

• Eugen Beutel: Squaring the Circle . 2nd Edition. Teubner, Leipzig 1920. (digitized version)
• Moritz Cantor : Lectures on the history of mathematics. Teubner, Leipzig 1880–1908, 4 volumes. (Digitized version)
• Helmuth Gericke : Mathematics in Antiquity and the Orient. Springer, Berlin 1984, ISBN 3-540-11647-8 .
• Helmuth Gericke: Mathematics in the West. Springer, Berlin 1990, ISBN 3-540-51206-3 .
• Thomas Little Heath: A History of Greek Mathematics . Volume 1, Clarendon Press, Oxford 1921. (Reprinted in Dover, New York 1981, ISBN 0-486-24073-8 .)
• Klaus Mainzer: History of Geometry. Bibliographisches Institut, Mannheim u. a. 1980, ISBN 3-411-01575-6 .
• Ferdinand Rudio : Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Teubner, Leipzig 1892. (digitized version)

To the transcendence of ${\displaystyle \pi }$

• Ferdinand Lindemann: About the number . ${\displaystyle \pi }$In: Mathematische Annalen 20 (1882), pp. 213–225 ( digitized version ).
• David Hilbert: About the transcendence of the numbers e and . ${\displaystyle \pi }$In: Mathematische Annalen 43 (1893), pp. 216-219 ( digitized version ).
• Lorenz Milla: The transcendence of and the squaring of the circle. ${\displaystyle \pi }$ arXiv.org , 2020.
• Paul Albert Gordan: Transcendence of e and . ${\displaystyle \pi }$In: Mathematische Annalen 43 (1893), pp. 222-224 ( digitized version ).
• Theodor Vahlen: Proof of Lindemann's theorem about the exponential function. In: Mathematische Annalen 53 (1900), pp. 457-460 ( digitized version ).

Entertainment math

• Underwood Dudley: Mathematics Between Insanity and Joke. Fallacies, False Evidence, and the Meaning of the Number 57 in American History, Birkhäuser, Basel 1995, ISBN 3-7643-5145-4 . (Original English title: Mathematical cranks )

Web links

Wikiversity: A Lecture on Squaring the Circle  - Course Materials

Commons : Squaring the circle  - collection of images, videos and audio files

Wiktionary: Squaring the circle  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Elementary Operations in Wikibooks  - Learning and Teaching Materials

Wikibooks: Squaring the Circle  - Learning and Teaching Materials

... with 245850922: 78256779, the reciprocal of a fraction by Johann Heinrich Lambert

• Squaring the circle - Article in MacTutor History of Mathematics archive (English)

Individual evidence

1. ↑ Detlef Gronau: The Rhind Papyrus. (PDF) Lecture on the early history of mathematics. Karl-Franzens-Universität Graz, 2009, p. 11 , accessed on March 2, 2020 . 
2. ↑ Jean Christianidis: ÁRPÁD SZABÓ / As has become the math to a deductive science? ; Classics in the History of Greek Mathematics, Springer Science & Business Media, 2013, pp. 68 ff. ( Limited preview in Google book search), accessed on February 22, 2020
3. ↑ Wolfgang Tzschoppe: 2.3 The number line fills up ; Structure of Mathematics - Mathematics of Structures, BoD - Books on Demand, 2012, p. 40 ff. ( Limited preview in Google book search), accessed on March 22, 2020.
4. ^ Andreas Büchter, Hans-Wolfgang Henn: 4.1.1 A brief historical overview ; Elementary Analysis: Von der Anschauung zur Theory, Springer-Verlag, 2010, p. 107 ff. ( Limited preview in the Google book search), accessed on March 22, 2020
5. ↑ Detlef Gronau: The classic problems of antiquity. (PDF) Lecture on the early history of mathematics. Karl-Franzens-Universität Graz, 2009, p. 32 , accessed on February 22, 2020 . 
6. ↑ Arthur Donald Steele: On the role of compasses and ruler in Greek mathematics . In: Oskar Becker (Ed.): On the history of Greek mathematics ; Wissenschaftliche Buchgesellschaft, Darmstadt 1965, pp. 146–202
7. ↑ Detlef Gronau: Athenian period (450-300 BC). (PDF) Lecture on the early history of mathematics. Karl-Franzens-Universität Graz, 2009, p. 31 ff. , Accessed on February 22, 2020 . 
8. ↑ Helmuth Gericke: 4. The squaring of the circle ; Mathematik in Antike und Orient, Springer-Verlag, 2013, p. 94 ( limited preview in the Google book search), accessed on February 23, 2020
9. ^ Paul Deussen: Anaxagoras ; General History of Philosophy, Volume 2, Leipzig: FA Brockhaus, 1911, pp. 124 ff. ( Limited preview in the Google book search), accessed on February 23, 2020
10. ^ Albin Lesky: The Enlightenment and its opponents: The specialist sciences ; History of Greek Literature, Walter de Gruyter GmbH & Co KG, 2015, p. 545 ( limited preview in Google Book Search), accessed on February 24, 2020
11. ^ Oskar Becker : 3. Lunulae Hippocratis ; The mathematical thinking of antiquity, Göttingen Vandenhoeck & Ruprecht, 1966, p. 58 ( limited preview in the Google book search), accessed on February 22, 2020
12. ↑ Christoph J. Scriba, Peter Schreiber: Möndchenquadratur des Hippokrates ; 5000 Years of Geometry: History of Cultures People, Springer-Verlag, 2013, p. 48 ( limited preview in Google book search), accessed on February 23, 2020
13. ↑ James Gow : A Short History of Greek Mathematics, Franco von Lüttich , 1884, Reprint: Cambridge University Press, 2010, pp. 162-164 ( limited preview in Google Book Search), accessed on February 23, 2020
14. ↑ Jean-Paul Delahaye: History of the number at the time of geometry ${\displaystyle \pi }$  ; - The story: From the French by Manfred Stern, Springer-Verlag, 2013, pp. 71 ff. ( Limited preview in Google book search), accessed on February 22, 2020 ${\displaystyle \pi }$
15. ↑ In English translation by Thomas Little Heath : Measurement of a Circle , The works of Archimedes, ed. In modern notation, with introductory chapters. University press, Cambridge 1897. P. 91 ff., (Digitized version)
16. ^ Haller, Rudolf (translator): XII.2. Circles are in proportion to the squares above their diameters. (PDF) Euclid: Elements of Stoicheia. Markgröningen: Edition Opera-Platonis, 2017, p. 2 ff. , Accessed on February 25, 2020 . 
17. ^ F. Rudio: III. The circumference of each circle is three times as large as the diameter and slightly larger ... Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 75 ff. , Accessed on March 2, 2020 . 
18. ↑ Eugene Pouch: Archimedes The squaring of the circle. 1920, 2nd edition. Teubner, Leipzig 1920. p. 14 ff. ( Digitized version )
19. ↑ In English translation by Thomas Heath: On Spirals , The works of Archimedes, ed. In modern notation, with introductory chapters. University press, Cambridge 1897. p. 151 ff., (Digitized version)
20. ↑ Hans-Dieter Rinkens: .3.2 Rectifying the circle with the help of the Archimedean spiral. (PDF) ie script winter semester 2017/18. 2017, p. 19 , accessed on March 2, 2020 . ${\displaystyle \pi }$ ${\displaystyle \pi }$ 
21. ^ ^{A b} Helmuth Gericke: Science in the Christian Occident (6th – 10th centuries), Franco von Lüttich ; Mathematics in the Occident: From Roman Surveyors to Descartes, Springer-Verlag, 2013, p. 75 ff. ( Limited preview in Google book search), accessed on February 25, 2020
22. ↑ Helmuth Gericke: Science in the Christian Occident (6th – 10th century), Franco von Lüttich ; Mathematics in the Occident: From Roman Surveyors to Descartes, Springer-Verlag, 2013, p. 74 ff. ( Limited preview in Google book search), accessed on February 23, 2020
23. ^ ^{A b} Helmuth Gericke: Science in the Christian Occident (6th – 10th centuries), Franco von Lüttich ; Mathematics in the Occident: From Roman Surveyors to Descartes, Springer-Verlag, 2013, p. 76 ff. ( Limited preview in the Google book search), accessed on February 23, 2020
24. ^ F. Rudio: § 8. The time of the Renaissance. Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 27-28 , accessed March 1, 2020 . 
25. ↑ FR Scherer: Comparison of three methods for the approximate rectification of circular arcs. (PDF) Naturforschende Gesellschaft in Zürich, 1929, p. 1 , accessed on February 22, 2020 . 
26. ^ F. Rudio: III Christian Huygens (1629–1695) About the size of the circle (De circuli magnitudine inventa). Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 83-131 , accessed February 25, 2020 . 
27. ↑ ^{a b} F. R. Scherer: Comparison of three methods for the approximate rectification of circular arcs. (PDF) Naturforschende Gesellschaft in Zürich, 1929, p. 2 , accessed on February 22, 2020 . 
28. ^ F. Rudio: III Christian Huygens (1629–1695) About the size of the circle (De circuli magnitudine inventa). Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, p. 130 , accessed February 25, 2020 . 
29. ^ Jean-Paul Delahaye: The story of the time of analysis ${\displaystyle \pi }$ ; - The story: Translated from the French by Manfred Stern, Springer-Verlag, 2013, p. 84 ( limited preview in the Google book search), accessed on February 23, 2020 ${\displaystyle \pi }$
30. ^ Katrin Plank: Representation as a continued fraction. (PDF) The fascination of numbers . Karl-Franzens-Universität Graz, 2015, p. 16 , accessed on February 22, 2020 . ${\displaystyle \pi }$ 
31. ^ Karl Helmut Schmidt: Too infinite ; Pi History and Algorithms of a Number, BoD - Books on Demand, 2001, p. 37 ( limited preview in Google Book Search), accessed on February 23, 2020
32. ↑ Rudolf Wolf: The reform of goniometry through and since Euler , handbook of astronomy, its history and literature, F. Schulthess, Zurich 1890, vol. 1, p. 177 ( digitized version )
33. ^ Franka Miriam Brückler: Origin of analytical geometry ; History of Mathematics Compact, Springer-Verlag, 2017, p. 83 ff. ( Limited preview in Google book search), accessed on February 22, 2020
34. ^ Franka Miriam Brückler: Origin of analytical geometry ; History of Mathematics Compact, Springer-Verlag, 2017, p. 85 ff. ( Limited preview in the Google book search), accessed on February 22, 2020
35. ↑ in detail, for example, from Felix Klein : Lectures on selected questions of elementary geometry . Teubner, Leipzig 1895 (digitized version)
36. ↑ Adalbert Kerber: Constructions with compasses and ruler. (PDF) Linear Algebra, WS 2002/2003. University of Bayreuth, September 4, 2004, p. 327 , accessed on February 22, 2020 . 
37. ^ Leonhard Euler: Introductio in analysin infinitorum . Lausanne 1748. German by H. Maser: Introduction to the analysis of the infinite . Springer, Berlin 1885. (Reprint of the first volume)
38. ↑ Edmund Weitz: The exponential function in the complex. Concrete math (not only) for computer scientists. Springer Link, August 9, 2018, p. 644 , accessed on February 23, 2020 . 
39. ↑ F. Rudio: § 12. The proof of the irrationality of the number by Lambert and Legendre. ${\displaystyle \pi }$Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 54 ff. , Accessed on March 2, 2020 . 
40. ^ F. Rudio: Legendre, proof that the ratio of the circumference to the diameter and the square of the same are irrational numbers. Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 165–166 , accessed March 3, 2020 . 
41. ^ F. Rudio: § 13. The discoveries of Liouville. Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 58-60 , accessed March 3, 2020 . 
42. ↑ Knut Smoczyk: Constructions with compasses and ruler ; Geometrie für dem Lehramt, BoD - Books on Demand, 2019, p. 238 ( limited preview in the Google book search), accessed on February 24, 2020
43. ↑ ^{a b} David J. Green: Transcendence of e and . ${\displaystyle \pi }$University of Jena, 2006, pp. 1 ff. , Accessed on February 24, 2020 . 
44. ↑ F. Rudio: Quadrature of the circle, fourth chapter. § 15. The final settlement of the problem, etc. Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, pp. 66-67 , accessed February 25, 2020 . 
45. ↑ David Hilbert: About the transcendence of e and . ${\displaystyle \pi }$DigiZeitschriften, 1893, pp. 216–219 , accessed on February 24, 2020 . 
46. ↑ Jean-Étienne Montucla: Histoire des recherches sur la quadrature du cercle . Paris 1754 (digitized version of the corrected new edition 1831)
47. ↑ JH Lambert: V. Provisional knowledge for those who are looking for the quadrature and rectification of the circle. Baytrags on the use of mathematics and its application. SUB, Göttinger Digitization Center, 1770, pp. 140 ff. , Accessed on March 9, 2020 . 
48. ↑ Augustus de Morgan: A Budget of Paradoxes. The Project Gutenberg EBook, 2007, p. Div. , Accessed on March 13, 2020 . 
49. ^ Histoire de L'Académie royale des sciences, année 1775 . Paris 1778, p. 61ff. ( Digitized version )
50. ^ F. Rudio: § 1. On the various causes of the great popularity of the problem. Archimedes, Huygens, Lambert, Legendre. Four treatises on circular measurement. Internet Archive, 1892, p. 4 , accessed March 3, 2020 . 
51. ↑ Collective of authors: Squaring the circle. retrobibliothek, Meyers Konversations-Lexikon, 1892, p. 756 , accessed on February 24, 2020 . 
52. ↑ Douglas M. Jesseph, reviewed by David Graves: Squaring the Circle: The War Between Hobbes and Wallis review. Mathematical Association of America, MAA REVIEW, July 27, 1999, accessed February 23, 2020 . 
53. ↑ JH Lambert: V. Provisional knowledge for those who are looking for the quadrature and rectification of the circle. Baytrags on the use of mathematics and its application. SUB, Göttinger Digitization Center, 1770, p. 143 ff. , Accessed on March 9, 2020 . 
54. ↑ Gotthold Ephraim Lessing: Auf den Herr M ** the inventor of the squaring of the circle ; Lessing's writings. First Part, LF Voss, 1753, p. 217 ( limited preview in Google book search), accessed on March 13, 2020
55. ↑ Ryan Schwier: Legislating Pi. Indiana Legal Archive, March 14, 2015, accessed February 23, 2020 . 
56. ^ Thomas Heath: VII. Special Problems, The squaring of the circle. A History of Greek Mathematics Volume 1. Internet Archive, 1921, pp. 220 ff. , Accessed on March 9, 2020 . 
57. ↑ Dante Alighieri, LG Blanc (translator) , The Divine Comedy - Paradise - Singing 33 , Operons, Stage Works with Music, accessed on March 10, 2020
58. ↑ ^{a b} James Joyce, Ulysses: Roman, Suhrkamp Verlag 2015 , (limited preview in Google book search), accessed on March 10, 2020
59. ↑ Éléonore Quinaux, the cross-reader: Leopold Bloom (Odysseus) ; Ulysses by James Joyce (reading aid): Detailed summary, personal analysis and interpretation, derQuerleser.de, 2018, p. 16. ( limited preview in Google book search), accessed on March 10, 2020
60. ↑ Helmuth Gericke: Albrecht Dürer: Vnderweysung der messung ; Mathematics in the Occident: From Roman Surveyors to Descartes, Springer-Verlag, 2013, p. 191. ( limited preview in Google book search), accessed on February 25, 2020
61. ↑ Dieter Grillmayer: 2. The approximate construction by Kochański:, In the realm of geometry: Part I: level geometry, BoD - Books on Demand, 2009, p. 49 ( limited preview in Google book search), accessed on February 23, 2020
62. ^ ^{A b} Ernest William Hobson : The First Period, Fig. 17. Squaring the Circle: A History of the Problem. In: Internet Archive. Cambridge University Press, 1913, p. 34 , accessed January 13, 2020 . 
63. ↑ Ian Stewart: 2nd Master of the Way Liu Hui ; The greats of mathematics: 25 thinkers who made history, Rowohlt Verlag GmbH, 2018, ( limited preview in Google book search), accessed on March 16, 2020
64. ^ ^{A b} Ernest William Hobson : The First Period Fig 19. Squaring the Circle: A History of the Problem. In: Internet Archive. Cambridge University Press, 1913, p. 35 , accessed March 1, 2020 . 
65. ↑ ^{a b} S. A. Ramanujan: Squaring the circle. In: Journal of the Indian Mathematical Society 5. The Institute of Mathematical Sciences, 1913, p. 132 , accessed July 29, 2019 . 
66. ↑ SA Ramanujan: Modular Equations and Approximations to . ${\displaystyle \pi }$12. Another curious approximation to is. In: Quarterly Journal of Mathematics. The Institute of Mathematical Sciences, 1914, pp. 350–372 , accessed July 29, 2019 . ${\displaystyle \pi }$ 
67. ↑ SA Ramanujan: Modular Equations and Approximations to . ${\displaystyle \pi }$In: Quarterly Journal of Mathematics. The Institute of Mathematical Sciences, 1914, pp. 350–372 , accessed July 29, 2019 . 
68. ↑ Eckard Specht: A.14 The arithmetic mean. University of Magdeburg, accessed April 25, 2020 . 
69. ↑ Louis Loynes: 2978. Approximate quadrature of the circle. The Mathematical Gazette, Volume 45. Cambridge University Press, 1961, p. 330 , accessed March 9, 2020 . 
70. ^ Johann Heinrich Lambert: Contributions to the use of mathematics and their application . Quadratur des Circuls, p. 157 Berlin, in Verlag der Buchhandlung der Realschule, 1770, accessed on July 11, 2016
71. ↑ Horst Hischer: 1 connection between quadratrix and trisectrix. (PDF) History of mathematics as a didactic aspect (2). Solution of classic problems. horst.hischer, 1994, p. 279 , accessed on February 20, 2020 . 
72. ↑ Horst Hischer: 2 A proposal for the treatment of Trisectrix and Quadratrix in the upper school. (PDF) History of mathematics as a didactic aspect (2). Solution of classic problems. horst.hischer, 1994, pp. 282 - 287 , accessed on February 20, 2020 . 
73. ↑ ^{a b} Mario Gerwig: The way to the Lehrstück, (8) retrospect and outlook ; Mathematics in the Occident: Understanding Evidence in Mathematics Lessons: Axiomatics, Pythagoras and Prime Numbers as Examples of Teaching Art Didactics, Springer-Verlag, 2015, p. 209 ( limited preview in Google book search), accessed on February 23, 2020
74. ↑ M. Laczkovich: Equidecomposability and discrepancy; a solution to Tarski's circle squaring problem. Journal for pure and applied mathematics. SUB, Göttinger Digitization Center, 1990, pp. 77–117 , accessed on March 10, 2020 . 
75. ↑ Marwin Wirtz: 2.3 Surface of the Lemniscate. (PDF) The Cassini curves and especially Bernoulli's lemniscates. University of Mainz, 2017, p. 9 , accessed on February 20, 2020 . 

This article was added to the list of excellent articles in this version on March 28, 2020 .