Quadrature the rectangle

The squaring of the rectangle is a classic task of geometry . With a ruler and compass, a square with the same area should be drawn from a given rectangle . In contrast to the squaring of the circle , which is insoluble, the squaring of the rectangle can be done in different ways.

Starting position

Right triangle

The starting point for the following two constructions are two mathematical laws , which go back to Euclid , of the right triangle , the law of heights and the law of legs .

In a right-angled triangle are a and b , the the right angle enclosing catheti and c the hypotenuse . Let h be the height on side c , and let p and q be the two hypotenuse segments. Then the following relationships apply:

${\ displaystyle h ^ {2} = p \ cdot q}$ (Euclid's theorem of elevation)

${\ displaystyle a ^ {2} = c \ cdot p}$ and (Euclid's set of cathets) ${\ displaystyle b ^ {2} = c \ cdot q}$

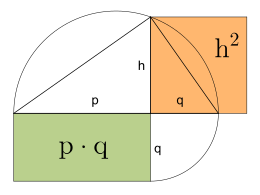
Method with the height theorem

Quadrature using the theorem of heights

Regardless of the proportions of the given (here green) rectangle: We assume that one side is the hypotenuse section p and the other side is the hypotenuse section q of a right triangle. Then we pivot the (here) shorter side of the rectangle by 90 ° and get the base of a right triangle. We draw a Thales circle over this base . The extension of the shorter side of the rectangle intersects the Thales circle and provides the height of the right-angled triangle with the hypotenuse sections p and q. If you now erect a square (here orange) above this height, it has exactly the same area as the given rectangle.

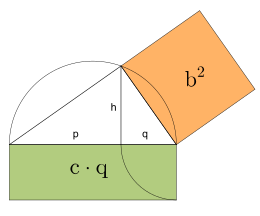
Method with the cathet set

Quadrature with the help of the catheter set

With the second method, one assumes that the longer side of the (here green) rectangle would extend over the entire base c of a right triangle. Then the shorter side of the rectangle is turned inwards by 90 °, it provides the hypotenuse section q and the base point of height h. Then draw a Thales circle over base c . The intersection of the height with the circular line results in the third triangular point, which results in the leg b. If you now build a (here orange) square over b, it has exactly the same area as the given rectangle.

Method with the secant-tangent theorem

Quadrature with the help of the secant-tangent theorem

The secant-tangent theorem can also be used to square the rectangle: In a given (here green) rectangle with length p and width q , let a length p also be identified as a segment PR . Let the segment QR be equal to the width q and be within PR . Let M _{1 be} the midpoint of the segment PQ . Let k ₁ of the circle with diameter PQ , and k ₂ of the circle with a diameter M ₁ R . Let T be an intersection of these circles. The angle M ₁ TR is right according to Thales' theorem, so RT is a tangent to k ₁ . According to the secant-tangent theorem, ( RT ) ² = p q .

Method with the tendon set

Quadrature with the help of the set of chords.
The gray rectangle b · c and the dashed lines are not required for the solution, they are only intended to clarify the solution, e.g. B. for which reason the distance BG one side a is the same area square.

One of the four best-known solutions for surface conversion is also one that can be represented with the aid of the set of tendons .
For the quadrature of a given (here blue) rectangle with length p and width q , first two corners of a long side are designated with A and B respectively. This is followed by the extension of the segment AB by the width q using the quarter circle, which results in the segment AC . After drawing in the center line of AC , the freely selectable point M is determined on the center line . Now draw a circle around point M with radius | MA |; hereby the segment AC becomes the first chord of the circle. It continues by increasing the diameter of the circle through the point B is drawn. The resulting line EF is the second chord of the circle. Both tendons intersect at point B , which in turn divides tendon AC into p and q and tendon EF into b and c . Finally, a vertical line is set up on the line EB , which runs from point B to the circular line and creates the intersection point G. The first side a of the sought-for square (here green) of the same area thus results as the segment BG .

As described, the chord EF is drawn through the center of the circle in the adjacent drawing . Due to this, there is the possibility (as shown), in addition to the rectangular area bc for the conversion into the square area a ² , to ^draw the right-angled triangle EFG with the height h = a and the square area h ^{2 in order} to clarify and justify the result . Seen all together, the connection between the set of tendons and the set of heights is clearly recognizable.

According to the law of chords:

{\ displaystyle {\ overline {AB}} \ cdot {\ overline {BC}} = {\ overline {EB}} \ cdot {\ overline {BF}}}

or.

{\ displaystyle p \ cdot q = b \ cdot c,}

it follows (as in Euclid's theorem of heights)

{\ displaystyle a ^ {2} = p \ cdot q,}

if the square root is taken from this, the side length a of the square is equal to the geometric mean of the length p + q.

{\ displaystyle a = {\ sqrt {pq}}}

Division into squares

Analogous to the squaring of the square , one can also consider the problem of dividing a rectangle into squares of different sizes (squaring the rectangle). The first solution was found in 1925 by the Polish mathematician Zbigniew Morón (1904–1971). He divided a 33 × 32 rectangle into 9 squares with sides 1,4,7,8,9,10, 14, 15, 18 and a 65 × 47 rectangle into 10 squares with sides 3,5,6,11, 17, 19, 22, 23, 24, 25. The first squaring of a square followed in 1939 by Roland Sprague and in 1940 by William Thomas Tutte and colleagues.

literature

Schülerduden - Mathematics I . Bibliographisches Institut & FA Brockhaus, Mannheim 2008, ISBN 978-3-411-04208-1 , pp. 193, 212, 415-417
Claudi Alsina, Roger B. Nelsen: Pearls of Mathematics: 20 geometric figures as starting points for mathematical exploratory trips . Springer, 2015, ISBN 978-3-662-45461-9 , pp. 31–32

Web links

Commons : Rectangle squaring - collection of images, videos and audio files

Eric W. Weisstein : Rectangle Squaring . In: MathWorld (English).
Euclid's Elements Second Book, The 14th Movement. - Quadrature of the rectangle in the elements of Euclid
About the rectangle that wanted to become a square (PDF)
Quadrature the rectangle on mathematische-basteleien.de

Individual evidence

↑ Emese Vargyas, Ysette Weiss-Pidstrygach: 5 History of Mathematics in Classes Using the Example of Sinews, pp. 279–283, see p. 281, Fig. 4. (PDF) In: What areas is the set of tendons? mathematica-didactica.com, 2015, accessed April 28, 2019 .

↑ John M. Lee: Axiomatic Geometry . Ed .: American Mathematical Society. Rhode Island 2013, p. 303 ff . ( Construction Problem 16:20 (Rectangle with a Given Area and Edge) [accessed May 5, 2017]).

↑ University of Magdeburg A.14 averages. Middle proportions, side 2, point and Image: b) (PDF) accessed on May 7, 2017

^ Clifford Pickover: The Math Book . Sterling Publ. 2012, p. 352

[1] Emese Vargyas, Ysette Weiss-Pidstrygach: 5 History of Mathematics in Classes Using the Example of Sinews, pp. 279–283, see p. 281, Fig. 4. (PDF) In: What areas is the set of tendons? mathematica-didactica.com, 2015, accessed April 28, 2019 .

[2] John M. Lee: Axiomatic Geometry . Ed .: American Mathematical Society. Rhode Island 2013, p. 303 ff . ( Construction Problem 16:20 (Rectangle with a Given Area and Edge) [accessed May 5, 2017]).

[Magdeburg-3] University of Magdeburg A.14 averages. Middle proportions, side 2, point and Image: b) (PDF) accessed on May 7, 2017

[4] Clifford Pickover: The Math Book . Sterling Publ. 2012, p. 352