Euclid

Euclid of Alexandria ( ancient Greek Εὐκλείδης Eukleídēs , Latinized Euclides ) was a Greek mathematician who probably lived in the 3rd century BC. Lived in Alexandria .
Life

Almost nothing is known about the life of Euclid. From a note with Pappos it has been concluded that he worked in Alexandria, Egypt. The dates of life are unknown. The assumption that he was around 300 BC. BC, is based on a list of mathematicians in Proklos , other evidence suggests, however, that Euclid was a little younger than Archimedes (approx. 285–212 BC).
From a position at Proklos it has also been concluded that he was around the year 360 BC. Was born in Athens , where he received his training at Plato's Academy and then worked in Alexandria at the time of Ptolemy I (approx. 367–283 BC).
It should not be confused with Euclid of Megara , as was often the case until the early modern period, so that the name Euclid of Megara also appeared on the titles of the editions of the elements.
Works
The surviving works cover all areas of ancient Greek mathematics: these are the theoretical disciplines arithmetic and geometry ( the elements , data ), music theory ( the division of the canon ), a methodical guide for finding planimetric problem solutions from certain secure starting points ( porisms ) as well as the physical or applied works ( optics , astronomical phenomena ).
In his most famous work Elements (ancient Greek Στοιχεῖα Stoicheia , “Beginnings”, “Principles”, “Elements”) he gathered the knowledge of Greek mathematics of his time. He showed the construction of geometric objects, natural numbers and certain sizes and examined their properties. For this purpose he used definitions, postulates (according to Aristotle's principles , which can be accepted or rejected) and axioms (according to Aristotle, general and indubitable principles). Many theorems of the elements apparently do not come from Euclid himself. His main achievement consists rather in the collection and uniform representation of mathematical knowledge as well as the strict argumentation , which became the model for later mathematics.
In addition to the elements , the data and the division of the canon , surviving writings from Euclid include : Optika , On the division of figures (preserved in extracts in an Arabic translation), Phainomena (geometric treatment of astronomy) (fragments edited by Johan Ludwig Heiberg ). Only the titles of other works are known: u. a. Pseudaria (fallacies), Katoptrika .
The elements were the basis of geometry lessons in many places well into the 20th century, especially in the Anglo-Saxon region.
Geometry - arithmetic - proportion theory
In addition to Pythagorean geometry, Euclid's elements in Book VII-IX contain Pythagorean arithmetic, the beginnings of number theory (which Archytas of Taranto already knew) and the concepts of divisibility and the greatest common divisor . To determine it, he found an algorithm , the Euclidean algorithm . Euclid also proved that there are infinitely many prime numbers , called Euclid's theorem after him . Euclid's music theory is also based on arithmetic. Book V also contains the Eudoxus doctrine of proportion , a generalization of arithmetic to positive irrational quantities .
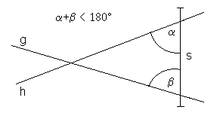
The well-known fifth postulate of planar Euclidean geometry (now called the axiom of parallels ) requires: If a line intersects with two straight lines and causes the angles that arise inside on the same side of and together are smaller than two right angles, then the two straight lines meet and on the same side of where the angles and lie. If two straight lines intersect a segment (or straight line) in such a way that the two angles enclosed by the segment and the two straight lines are smaller than 180 °, then the two straight lines intersect on this side and delimit together with the segment (or third straight line) a triangle.
The preoccupation with the axiom of parallels is of great importance for the history of science because it has contributed a great deal to the specification of mathematical concepts and methods of proof. In the course of this, the inadequacy of the Euclidean axioms became apparent in the 19th century. A formal axiomatic of Euclidean geometry can be found in David Hilbert's work Foundations of Geometry (1899), which led to many further editions and subsequent research. For the first time, a complete structure of Euclidean geometry is carried out, until the realization that every model of Hilbert's system of axioms is isomorphic to the three-dimensional real number space with the usual interpretations of the basic geometric concepts (such as point, line, plane, length, angle, congruence, Similarity etc.) in analytical geometry. Since ancient times, many important mathematicians have tried in vain to prove the axiom of parallels with the other axioms and postulates (it would then be dispensable). It was not until the 19th century that the axiom of parallels was indispensable with the discovery of a non-Euclidean geometry by Bolyai and Lobachevsky . The Poincaré half-plane H ( Henri Poincaré ) is a model for such an axiom system in which the parallel axiom does not apply. Thus the axiom of parallels cannot be deduced from the other axioms (see non-Euclidean geometry ).
Music theory
In Euclid's music theory work Die Teilung des Canon (Greek Katatomē kanonos , Latin Sectio canonis ), which can be classified as authentic, he took up Archytas' music theory and placed it on a more solid acoustic basis, namely on frequencies of vibrations (he spoke of Frequency of movements). He generalized Archytas' theorem about the irrationality of the square root and proved in general the irrationality of any roots . The reason for this generalization is its antithesis to the harmony of Aristoxenus , which is based on rational multiples of the tone (semitone ... nth tone). Because in the Pythagorean harmony the tone ( whole tone ) has the proportion 9: 8, which led Euclid to his antithesis "The tone cannot be divided into two or more equal parts"; however, it assumes commensurable frequencies that were accepted in Pythagorean harmony up to the end of the 16th century ( Simon Stevin ). He based the antithesis “The octave is smaller than 6 whole tones” on the calculation of the Pythagorean comma . Euclid's division of the canon also contains - as its title indicates - the oldest traditional representation of a tone system on the canon , a divided string, namely a Pythagorean reinterpretation of the complete diatonic tone system of Aristoxenus. Euclid's tone system was handed down through Boethius ; in the tone letter notation Odos, it became the basis of the modern tone system.
Eponyms
The following mathematical structures are named after Euclid:
- Euclidean distance , the length of the direct connection between two points in a plane or in space
- Euclidean algorithm , a method for computing the greatest common divisor of two natural numbers
- Euclidean geometry , the descriptive geometry of plane or space
- Euclidean solid , an ordered solid in which every nonnegative element has a square root
- Euclidean norm , the length of a vector in a plane or in space
- Euclidean space , the intuition space , a real affine space with the standard scalar product
- Euclidean relation , a relation for which the following applies: if two elements are each related to a third, then they are also related to each other
- Euclidean ring , a ring in which division by remainder is possible
- Euclidean tools , the permitted actions in construction with compasses and ruler
In addition, the following mathematical theorems and proofs are named after Euclid:
- Euclid's proof of the irrationality of the root of 2 , the first contradiction proof in the history of mathematics
- Euclid's theorem of heights : In a right-angled triangle, the square above the height is equal in area to the rectangle from the hypotenuse sections
- Euclid's theorem of catheters : In a right triangle, the cathetus squares are equal to the product of the hypotenuse and the associated hypotenuse section
- Euclid's Lemma : If a prime number divides a product of two numbers, then also at least one of the two factors
- Euclid's theorem : There are infinitely many prime numbers
Also named after Euclid:
- Euclides (moon crater) , a crater on the front of the moon
- (4354) Euclides , a main belt asteroid
Editions and translations
- Johan Ludvig Heiberg , Heinrich Menge (Ed.): Euclidis Opera Omnia. 9 volumes, Teubner, Leipzig 1888–1916 (Greek / Latin), more precisely 8 volumes with a supplement (the commentary on the elements of Al-Nayrizi in the translation of Gerhard von Cremona, edited by Maximilian Curtze )
- Euclid: The elements . Books I – XIII. Ed. U. trans. v. Clemens Thaer . (= Ostwald's Class of Exact Science 235). 4th edition. Harri Deutsch, Frankfurt am Main 2003, ISBN 3-8171-3413-4 .
- Euclid: The thirteen books of Euclid's elements . Ed. U. trans. v. Thomas Heath , 3 volumes, Cambridge University Press 1908, reprint Dover 1956 (English translation with extensive commentary and introduction to Euclid)
- Euclides: Data . The data of Euclid, after Menges text from d. Greek trans. u. ed. v. Clemens Thaer. Springer, Berlin 1962.
- The Medieval Latin Translation of the Data of Euclid. Translated by Shuntaro Ito, Tokyo University Press, 1980, Birkhauser, 1998.
- Euclid: Sectio canonis. newly edited, translated and commented in: Oliver Busch: Logos syntheseos. The Euclidean Sectio Canonis, Aristoxenus, and the role of mathematics in ancient music theory. Hildesheim 2004, ISBN 3-487-11545-X .
- Paul ver Eecke Euclide, L'Optique et la catoptrique. Paris, Bruges 1938 (French translation of optics )
literature
Overview representations in manuals
- Ivor Bulmer-Thomas , John Murdoch: Euclid. In: Dictionary of Scientific Biography . Volume 4, Charles Scribner's Sons, New York 1981, ISBN 0-684-16964-9 , pp. 414-459
- Menso Folkerts , Frieder Zaminer : Eukleides [3]. In: The New Pauly (DNP). Volume 4, Metzler, Stuttgart 1998, ISBN 3-476-01474-6 , Sp. 238-243.
- Bernard Vitrac: Euclide. In: Richard Goulet (ed.): Dictionnaire des philosophes antiques . Volume 3, CNRS Éditions, Paris 2000, ISBN 2-271-05748-5 , pp. 252-272
- Hans-Joachim Waschkies : Euclid. In: Hellmut Flashar (ed.): Outline of the history of philosophy . The philosophy of antiquity , Volume 2/1, Schwabe, Basel 1998, ISBN 3-7965-1036-1 , pp. 372–392
- Hans Wussing : Euclid. In: Arnold Wußing (Ed.): Biographies of important mathematicians. Berlin 1983.
Overall presentations and investigations
- Benno Artmann : Euclid: The creation of mathematics. Springer, 1999.
- Jürgen Schönbeck: Euclid: Around 300 BC. Chr. Springer, 2002, ISBN 3-7643-6584-6 .
- Peter Schreiber : Euclid. Teubner, Leipzig 1987.
- Christoph J. Scriba , Peter Schreiber: 5000 years of geometry. History, Cultures, People , Springer, Berlin 2005, ISBN 3-540-22471-8 , pp. 49-65 (the elements of Euclid and other writings as well as their context and reception in the further development of geometry in the further course of the book)
reception
- Diego De Brasi: Euclid. In: Peter von Möllendorff , Annette Simonis, Linda Simonis (ed.): Historical figures of antiquity. Reception in literature, art and music (= Der Neue Pauly . Supplements. Volume 8). Metzler, Stuttgart / Weimar 2013, ISBN 978-3-476-02468-8 , Sp. 433-438.
- Max Steck : Bibliographia Euclideana. The spiritual lines of tradition in the editions of the "Elements" of Euclid (around 365-300). Manuscripts, incunabula, early prints (16th century). Critical editions of the 17th – 20th centuries Century. Editions of the Opera Minora (16th – 20th centuries). Reprint, ed. by Menso Folkerts. Gerstenberg, Hildesheim 1981.
Arabic tradition
- Jan Hogendijk : The Arabic version of Euclid's 'On divisions'. In: Vestigia mathematica. Amsterdam 1993, pp. 143-162.
- Jan Hogendijk: On Euclid's lost 'Porisms' and its Arabic traces. In: Boll. Storia Sci. Mat. Volume 7, 1987, pp. 93-115.
Web links
- John J. O'Connor, Edmund F. Robertson : Euclid of Alexandria. In: MacTutor History of Mathematics archive .
- Literature by and about Euclid in the catalog of the German National Library
- Works by and about Euclid in the German Digital Library
- The elements of Euclid, Euclid: Stoicheia , books 1 to 12, completely in German.
- Perseus Euclid . Informative page from Perseus with translation and further sources, as well as further links.
- Euclid's Elements , all 13 books in English.
- Euclid's Elements , all 13 books in Greek with the Latin translation of Heiberg. (PDF)
- Text editions (ancient Greek, Arabic, English translations), Amund Bjørsnøs et al., Oslo Arabic Seminar.
- The six first books of Evclidis, Deß Highly Learned Famous, Greek Philosophi and Mathematici: From the Beginnings and Fundamentals of Geometriae . Amsterdam 1618, online edition of the Saxon State Library - Dresden State and University Library
- Euclidis Megarensis… sex libri priores, de Geometricis principiis . Basileae 1550, online edition of the Saxon State Library - Dresden State and University Library
- Euclidis Megarensis Mathematici Clarissimi Elementorum geometricorum Lib. XV . Basileae 1537, online edition of the Saxon State Library - Dresden State and University Library
- Elemental Geometricum . Argentorati 1529, online edition of the Saxon State Library - Dresden State and University Library
- Elementorum Libri XV . Coloniae 1627, online edition of the Saxon State Library - Dresden State and University Library
Remarks
- ↑ Pappos, Mathematical Collections 2,33–34.
- ↑ To be found in Proklos' work: Commentary on the first book of Euclid's "Elements" .
- ↑ Hans-Joachim Waschkies: Euclid. In: Hellmut Flashar (ed.): Outline of the history of philosophy . The philosophy of antiquity. Volume 2/1, Schwabe, Basel 1998, pp. 372–392, here: p. 372.
- ↑ Wilfried Neumaier: What is a sound system? Frankfurt am Main / Bern / New York 1986, chap. 6, The "Division of the Canon" of the Euclid
- ↑ Oliver Busch: Logos Synthesis. The Euclidean Sectio Canonis, Aristoxenus and the role of mathematics in ancient music theory. Berlin 1998, also Mag. Writing as Volume X of the publications of the State Institute for Music Research Prussian Cultural Heritage
| personal data | |
|---|---|
| SURNAME | Euclid |
| ALTERNATIVE NAMES | Euclid of Alexandria; Eukleidēs (ancient Greek); Εὐκλείδης |
| BRIEF DESCRIPTION | Greek mathematician |
| DATE OF BIRTH | around 365 BC Chr. |
| DATE OF DEATH | around 300 BC Chr. |






![{\ sqrt [{n}] {{\ tfrac {m + 1} {m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca3864b8b0e7089d0adf4aa06c0952e392781d5d)
