Diatonic
Diatonic (from ancient Greek διάτονος diátonos "going through whole tones", to διά "through" and τόνος "tension, tone"), a term mostly used adjectivally in music theory , characterizes certain tone relationships in tone systems and scales . Diatonic scales, for example, are special scales composed of whole and semitone steps, usually seven-step scales. Since the early Middle Ages, diatonic scales formed the basis of Western music, initially in the form of the church keys , later asMajor-minor system . At the turn of the 20th century, some of the composers abandoned the diatonic major-minor tonality.
In addition to the concept of the diatonic scale, there is that of the diatonic semitone ; one speaks of the diatonic semitone d-es in contrast to the chromatic semitone d-dis. There are also diatonic tetrachords , which are defined as four- tone sequences, consisting of two whole-tone steps and a semitone step.
Diatonic scale
Definition via root tones
Diatonic scales are mostly seven- step ( heptatonic ) scales that divide the octave space into five whole and two semitone steps. They differ from non-diatonic ladders by the following necessary features:
- All scales are derived from different root tones , which is reflected externally in the fact that their names all start with different letters.
- There are no excessive or decreased intervals between adjacent levels .
For example:
- CDEFGAH
- H - C is - D is - E - F is - G is - A is
- D es - E s - F - G es - A s - B - C
The “classical” diatonic scales ( major , minor and the church modes ) also meet the condition that they can be composed of two diatonic tetrachords (with the addition of an additional whole step). The tones of these scales can also be obtained by layering fifths (see below ).
Broadened conceptions
As an extension of this original strict definition, scales that only meet the condition of dividing the octave into five whole tones and two semitones are sometimes called diatonic today. Examples of this are the acoustic and the altered scale .
In addition, according to today's understanding, scales that contain fewer than seven tones can also be viewed as diatonic, such as B. the anhemitonic-pentatonic ladders, which divide the octave space into three whole steps and two thirds .
Examples
The most famous and most important diatonic scales today are the major and the ( natural ) minor scales :
with the following distribution of whole and semitone steps:

| C major | c ′ | d ′ | e ′ | f ′ | G' | a ′ | H' | c " | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tone step | Whole tone | Whole tone | halftone | Whole tone | Whole tone | Whole tone | halftone | |||||||||
| C minor | c ′ | d ′ | it' | f ′ | G' | as ′ | b ′ | c " | ||||||||
| Tone step | Whole tone | halftone | Whole tone | Whole tone | halftone | Whole tone | Whole tone | |||||||||
The diatonic scales in the narrower sense (“classical” diatonic scales) also include the church tones and the modal scales that are based on them today .
In a broader sense (see above under "Definition") these scales are also diatonic:
- the melodic minor scale upwards
- the altered scale used primarily in jazz
- the acoustic scale
- the anhemitonic-pentatonic ladders
Demarcation
These scales are not diatonic or not fully diatonic:
- the harmonic minor scale because it contains an excessive second ( hiatus )
- the gypsy scales as they contain excessive seconds ( hiatus )
- the whole tone scale, since the last whole step required to reach the octave is actually a diminished third (with a sharp-c notation starting from c)
- the chromatic scale
- the modes with limited transposition possibilities by Olivier Messiaen
Diatonic intervals
Diatonic intervals are those that are contained in a diatonic scale. In detail these are: pure prime , fourth , fifth and octave , minor and major second , third , sixth and seventh . The tritone is also part of the diatonic ladder, but is determined as an excessive fourth, i.e. as a chromatic variant of the pure fourth, and is not counted among the diatonic intervals.
In contrast to chromatic (excessive or diminished) intervals, in tonal music diatonic intervals are considered to be immediately understandable. For the distinction between diatonic and chromatic intervals, it does not matter whether the concerned tone accidentals have or not. The only decisive factor is whether the interval in question is part of a diatonic scale or not.
Examples:
- The minor third in c-es is a diatonic interval that occurs in C minor, E flat major or B flat major, among others. With enharmonic reinterpretation of the E flat to D flat, this becomes a chromatic interval: the excessive second C flat, which is not included in any diatonic scale.
- The minor second in c-des is diatonic, while the excessive prime in c-sharp is chromatic. The small second is also called a diatonic semitone , and the excessive prime is called a chromatic semitone .
The distinction between chromatic and diatonic intervals is only acoustically real when using pure tunings , whereas with today's common tuning - a compromise in intonation - the audible difference disappears. It then only exists in the notation, but is indispensable for understanding musical relationships in the major-minor tonality .
Derivation method
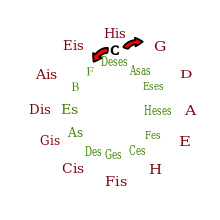
The designation diatonic only represents a demarcation from chromatics; how the scales are constructed is not yet determined. These can be derived from a distance, harmonic or melodic. A more precise, narrow definition of the term depends on the perspective of the respective music theorist.
One of the possible derivations is based on fifths in the circle of fifths , one also speaks of fifths stratification (or fifths stratification ). Starting from C in the circle of fifths one step downwards (counterclockwise) to F. Upwards (clockwise) one arrives at G, D, A, E, H (see picture on the right). In total, these are all notes of the C major scale.
Another common derivation is based on a certain sequence of whole and semitone steps, e.g. B. for major: whole tone - whole tone - semitone - whole tone - whole tone - whole tone - semitone (see picture on the left).
Hermann Grabner's (1886–1969) definition as well as the definition by Johann Georg Sulzer (1771) are much more detailed.
Moods
The tunings of the seven-step diatonic major scale are closely related to the derivation methods.
The Pythagorean tuning results from the stratification of fifths and is the tuning with the pitches Q 0 , Q 2 / O, Q 4 / O 2 , Q -1 O, Q 1 , Q 3 / O, Q 5 / O 2 , where O is the Octave and Q denote the fifth.
The pure tuning is that tuning in which the pitch levels have the frequency ratios 1: 1, 9: 8, 5: 4, 4: 3, 3: 2, 5: 3, 15: 8.
The equal temperament is that atmosphere in which the pitches, the frequency ratios H 0 , H 2 , H 4 , H 5 , H 7 , H 9 , H 11 have, where H denotes the root 12 of Figure 2.
History
Antiquity
In the music of ancient Greece (probably because of the exclusive unanimity), the diatonic, the chromatic and the enharmonic appeared as tone genders. In Aristoxenos , diatonic scales are those in which two or three whole tones alternate between the two semitones. Some of the oldest sources on diatonic scales go back to Greek philosophers and mathematicians. See also:
- Philolaos , section music theory
- Archytas , Music section
- Aristoxenos , section harmonics
- Euclid , section music theory
In late antiquity, Boëthius (around 500) described the Pythagorean tone sequence, but still used different letters to designate tones related to octaves.
middle Ages
Odo von Cluny (878 to 942) simplified the spelling. Guido of Arezzo (around 1025) wrote this as follows.
| Spelling after Odo | Γ | A. | B. | C. | D. | E. | F. | G | a | ♭ | ♮ | c | d | e | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| today's spelling | G | A. | H | c | d | e | f | G | a | b | H | c ′ | d ′ | e ′ | ... |
This is the Pythagorean tone sequence, in which the (Pythagorean) whole tone has the frequency ratio 9: 8 (204 cents ) and the semitone (fourth - 2 * pyth. Whole tone), also called Leimma , has the frequency ratio of 256: 243 ( 90 cents).
The church modes , for example, Doric: DEFG ahc then comprised seven tones of an octave. Guido von Arezzo (around 1025) laid the foundation for this by introducing staves and solmization (see Guidonic hand ).
Worldwide distribution
The diatonic scales expanded to twelve semitones per octave became more popular than others worldwide; so also in Egypt, India and China, while Arabic music with 24 intervals per octave , Indian with 66 or 22 micro-tones per octave and pentatonic Chinese can hardly be heard in the West.
Michael Schmidt-Salomon attributes this to internal musical reasons with an evolutionary-humanistic justification . The higher distribution is not the result of cultural imperialism , but a selection advantage of the Pythagorean scale, especially since the system was improved again in the 17th century with the well-tempered or equal mood . This makes it particularly suitable for creating new styles, while other systems can only be expanded to a limited extent.
Musicologist Robert Jourdain describes it as follows:
"The division of the tone space into twelve sections is obviously just right: the brain could no longer easily categorize additional tones, and with less one could not build a differentiated harmonic system."
Other musicologists consider this simplification to 12 semitones to be a gross disregard for intonation .
Ross W. Duffin writes:
"Regardless of how masterful today's musicians are, they no longer hear the bad major third of the equal tuning."
And the cellist Pablo Casals gives the advice:
“Don't be shocked if you have a different intonation than the piano. It's because of the piano, which is out of tune. The piano with its equal tuning is a compromise in terms of intonation. "
Diatonic hand pull instruments
The term “diatonic” is also often applied to hand- pulled instruments that reproduce different tones when pulled and pushed. In this case, “alternating tones” would be more precise, since the alternating tones need not be diatonic.
literature
- Zsolt Gárdonyi, Hubert Nordhoff: Harmonics. Möseler, Wolfenbüttel 2002, ISBN 3-7877-3035-4 , pp. 242-243.
References and comments
- ↑ Diatonic . In: Wilibald Gurlitt , Hans Heinrich Eggebrecht (Ed.): Riemann Musiklexikon . 12th, completely revised edition. Tangible part: A-Z . Schott, Mainz 1967, p. 224 .
- ↑ In ancient Greek music theory , τόνος was understood to mean the whole tone in the narrower sense, therefore διάτονος : “through whole tones (going)”. The latter refers to the diatonic tone system or the relevant diatonic tetrachord , which tries to fill the frame interval of a pure fourth "going through whole tones", but with a remainder in the form of a semitone ( Diesis , later called Limma ).
- ↑ The interpretation can also start from the verb: from the Greek δια "through" and τείνω "tighten, tighten, relax". If one understands by “tensioning” the tensioning and tuning of the strings of a lyre or kithara , then διατε freiνω can be freely translated as “through a tuning” or “through a key”.
- ↑ sound system . In: Wilibald Gurlitt , Hans Heinrich Eggebrecht (Ed.): Riemann Musiklexikon . 12th, completely revised edition. Tangible part: A-Z . Schott, Mainz 1967, p. 970 .
- ↑ Marc Honegger, Günther Massenkeil (ed.): The great lexicon of music. Volume 8: Štich - Zylis-Gara. Updated special edition. Herder, Freiburg im Breisgau a. a. 1987, ISBN 3-451-20948-9 , p. 148 f.
- ↑ scale . In: Wilibald Gurlitt , Hans Heinrich Eggebrecht (Ed.): Riemann Musiklexikon . 12th, completely revised edition. Tangible part: A-Z . Schott, Mainz 1967, p. 968 .
- ↑ For example, described by Guido von Arezzo (992-1050).
- ↑ In contrast to Brahms and Wagner, a bitter dispute was fought. Wagner retains the popular and historical diatonic, but finds his own chromatic tonal language in Tristan, for example. The “Brahmsians”, on the other hand, maintain the diatonic with recourse to the church modes and counterpoint. The twelve-tone technique developed by Arnold Schönberg from 1906 is in complete contrast to the diatonic.
- ↑ These criteria are only sufficient for the existence of a diatonic scale if one does not place any further demands on such a scale than dividing the octave space (somehow!) Into five whole tones and two semitones.
- ↑ Marc Honegger, Günther Massenkeil (ed.): The great lexicon of music. Volume 2: C - Elmendorff. Updated special edition. Herder, Freiburg im Breisgau a. a. 1987, ISBN 3-451-20948-9 , p. 312.
- ^ Hermann Grabner: General music theory. Bärenreiter, Kassel 2004, ISBN 3-7618-0061-4 .
- ↑ Text log: Johann Georg Sulzer: Diatonisch , seen September 16, 2010.
- ^ Walter Bühler: Calculating with musical intervals, scales and moods. PL Academic Research, 2014, ISBN 978-3-631-65059-2 , §17.1.
- ↑ Me. Hermesdorff (ed.): Micrologus Guidonis de disciplina artis musicae, ie Guido's short treatise on the rules of musical art. Grach, Trier 1876, p. 17 ( Textarchiv - Internet Archive ).
- ↑ Me. Hermesdorff (ed.): Micrologus Guidonis de disciplina artis musicae, ie Guido's short treatise on the rules of musical art. Grach, Trier 1876, p. 21. Quotation: “These length measures result in the following relationships for the intervals included in the tone series: Small seconds BC EF = 243: 256; Major seconds Γ-A, AB, etc. 8: 9; minor third AC, DF etc = 27:32; major third CE, Fa = 64:81; pure quart Γ-C, CF etc = 3: 4; perfect fifth Γ-D, CG etc = 2: 3; minor sixth EC = 81: 128; major sixth Γ-E, Ca etc = 16:27; minor seventh Γ-F = 9:16; major seventh C- ♮ = 128: 243; Octave Γ-G = 1: 2; large quart F- ♮ = 512: 729; small fifth (as the inversion of the tritone) = 729: 1024. "
- ↑ The tone Γ - an octave below G - was used to determine the fourth from Γ to C. This circumvented the construction of the practically impossible ratio c: A = 32:27 or even c: H = 256: 243. ( Text archive - Internet Archive ).
- ↑ Michael Schmidt-Salomon : Hope human. A better world is possible. , Piper Verlag, Munich 2014, pp. 199-200.
- ↑ Robert Jourdain: The well-tempered brain: How music arises and works in the head. Spektrum Verlag, Heidelberg 1998, p. 110.
- ^ Ross W. Duffin, How Equal Temperament Ruined Harmony (And Why You Should Care). See 30 W. W. Norton & Company , New York NY 2007, ISBN 978-0-393-06227-4 ( excerpt ).
- ^ The Way They Play (1972).



