scale

In music, a scale or ( tone ) scale is a series of tones arranged according to the pitch , which is limited by frame tones , beyond which the tone series can usually be repeated.

In most cases a scale has the range of an octave and in many cases follows a heptatonic scale structure. How a scale is structured as a manifestation of tonality is determined in the tone system .

→ Main articles : mood (music) , key  and tone system

The most common European and other scales are based on five or seven tones within the octave, which pitches are called. Diatonic scales in major and minor or the church scales are widely used . Scales are defined by pitch intervals . The notes contained in the actual scale is known as diatonic tones.

In non-European music such as classical Arabic or Indian music there are tone systems and scales that divide the tone space differently, for example mugam , maqam or raga .

example

C major scale

Keyboard over two octaves

As an example, one of the most common scales in Central Europe today: the major scale. It consists of tones at a distance:

Whole step - whole step - semitone - whole step - whole step - whole step - semitone

A scale defined in this way can be started on any note. By specifying a specific starting tone ( root note ), a key such as C major , D major , etc.

C major: CDEFGAHC

D major: DE-Fis-GAH-Cis-D

The ladder's own tones of C major are also called master tones and correspond to the white keys on a keyboard .

On a keyboard, the black keys are assigned “raised” or “lowered” ladder-specific tones. In the German-speaking world, they are called raised C sharp, D sharp, F sharp, G sharp and A sharp and lowered D flat, Eb, G flat, A flat and B. In other cultural areas the tones are referred to by other names . Today, in most cases, the equal tuning is used on keyboard instruments , so the semitones can be exchanged enharmonically . This means that on a keyboard there is only one key for C sharp and D flat, for D flat and E flat, etc. Thus each corresponds to the twelve ( with the publication of the Werckmeister tuning in 1691) (in non-European tone systems also more, mostly 20-24 ) possible tones within an octave of a certain frequency.

→ Main article : Frequencies of equal tuning

In the following, if not mentioned otherwise, it is assumed that the tuning is equal, since this is the most common tuning today. Tones can then be exchanged enharmonically.

Examples of scales

• The scales of the pentatonic ( pentatonic scale with five notes or pitches):
  • ordinary major and minor pentatonic scales
  • The twelve Lü of Chinese music
  • Japanese pentatonic scale
  • Indian pentatonic scale
  • the slendro of the island of Java,
  • the pélog from Indonesia
• The whole tone scale ( hexatonic , six tones)
• The heptatonic scales (seven notes):
  • The major scale
  • The different minor scales (pure or natural minor, harmonic minor, melodic minor)
  • The church scales ( Dorian , Phrygian , Lydian , Mixolydian , Locrian , etc.)
  • The acoustic scale
  • The Phrygian dominant scale
  • The gypsy scales ("Gypsy major" and "Gypsy minor") with two one and a half steps
  • The harmonic major scale
  • The Mi- Shebach scale
  • The altered scale
  • The enigmatic ladder
• The diminished scale ( octatonic , eight tones, also called whole-tone-semitone scale or semitone-whole-tone scale )
• The chromatic scale (twelve notes in the tempered, European major-minor system)
• Other:
  • The early Greek aulos modes
  • The ragas of Indian music
  • The scales of the Persian Dastgah system
  • The blues scale (see also Blue Notes ), hovering between major and minor by "clouding" of the third and seventh stages of the major scale
  • The Shepard Scale

Pictorial representation of scales

There are different pictorial representations that - depending on what is to be clarified - are more or less suitable for clarifying certain relationships. In many cases, the representations are based on the grip patterns or tablatures of instruments. A few representations have also been introduced by well-known music theorists in their works in order to clarify certain theories. There are no representations that do justice to all aspects.

The harmoniously pure clay net

→ Main article : The Euler's Tonnetz

Scheme of a harmoniously pure tone network.

After Leonhard Euler , published in "Novi Commentarii academiae scientiarum Petropolitanae".

It not only depicts the tone relationships of the harmonic-pure tuning (the tones a, e and h sound a syntonic comma lower than in the Pythagorean chain of fifths ), but also very vividly the chord stock of each major or minor scale, which is especially true for harmonic and melodic minor is very useful. In fact, our common major and minor scales are just as intended , as gebrachtem in an octave supply of tones of the main harmonies (here: F major (left), C Major (center), G major (right), ...). In addition to harmonies, in each case there next to see: Carl Dahlhaus “Investigations into the Origin of Harmonic Tonality” In addition, with this tonal network even functionally harmonious relationships can be clearly illustrated; see: Renate Imig: Systems of functional designation in harmony teachings since Hugo Riemann

Representation in tempered semitone circles

Halftone circle after Guerino Mazzola

The inner symmetry (here as-d) is immediately apparent, which is particularly helpful when displaying the modes with limited transposition options. This graphic can also be expanded to show twelve-tone rows or chords. However, in this version this is tied to a keynote. You can simply leave out the tone letters as long as you can see where the scale begins and where it ends. This representation assumes the temperature is equal , which is of course not historically correct for church modes. But instead of the semitone circle, you could also use the fifth spiral or similar. use. It looks like tones are skipped and no distinction is made between diatonic and chromatic semitone steps. However, this is the case in any representation based on the tempered scale.

Key assignments as a template

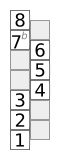
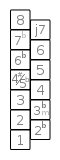
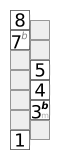
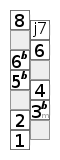
The following graphics depict various scales based on the not very common key assignment of 6-plus-6 instruments .

The diagram opposite shows a chromatic scale . The bottom box represents the root note . The boxes above are the notes of the scale, named after their interval to the root note. The “ladder” should therefore be read in a zigzag shape. The top box represents the same note as the root, only an octave higher.

The scheme enables patterns to be remembered. The patterns are distance patterns, semitones , whole steps and three semitones can easily be recognized.

Major ( Ionian ) listening ? / i	pure minor ( Aeolian ) listening ? / i	harmonic minor listening ? / i	Listen to gypsy minor ? / i	listening to melodic minor ? / i
Listen to Dorian ? / i	Listen to Phrygian 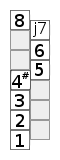? / i	Listen to Lydian ? / i	Listen to Mixolydian ? / i	Locrian Listen ? / i
Listen chromatically ? / i	Listen to whole tone scale ? / i	Listen to major pentatonic scales ? / i	Listen to minor pentatonic scales ? / i	Listen to the Altered Scale ? / i
Decreased scale , 1st form Listening ? / i	Reduced scale , 2nd form listening ? / i	Phrygian dominant scale (Spanish / Jewish scale) (e.g. Hava Nagila ) Listen ? / i	Listen to Gypsy major (Arabic scale) ? / i	Wed Shebear after listening ? / i

See also

• Natural tone series
• Modal scales
• Greek popular music scales

literature

• Wieland Ziegenrücker: General music theory with questions and tasks for self-control. German Publishing House for Music, Leipzig 1977; Paperback edition: Wilhelm Goldmann Verlag, and Musikverlag B. Schott's Sons, Mainz 1979, ISBN 3-442-33003-3 , pp. 78-103 ( The scales ).

Web links

Wiktionary: scale  - explanations of meanings, word origins, synonyms, translations

• PowerPoint presentation for creating scales
• Database of all 2048 possible scales in 12 tones in .xls and FileMaker format, system for categorizing scales
• Harmony workshop # 1 - major scale on bonedo.de

• Audio samples:
  • All important scales / explanations, sheet music and audio examples
  • Some scales with midi audio samples

• Moods:
  • Scala - program for creating, analyzing and manipulating scales and moods (freeware)
• Scales and scales on musikanalyse.net

Individual evidence

1. ↑ Willibald Gurlitt, Hans Heinrich Eggebrecht (Ed.): Riemann Musiklexikon . Material part . 12th edition. B. Schott's Sons, Mainz 1967, p. 968 .
2. ↑ Wieland Ziegenrücker: General music theory with questions and tasks for self-control. German Publishing House for Music, Leipzig 1977; Paperback edition: Wilhelm Goldmann Verlag, and Musikverlag B. Schott's Sons, Mainz 1979, ISBN 3-442-33003-3 , p. 99 f.
3. ^ Leonhard Euler : De harmoniae veris principiis per speculum musicum repraesentatis
4. ^ Novi Commentarii academiae scientiarum Petropolitanae 18, St. Petersburg, 1774
5. ↑ Carl Dahlhaus : Investigations into the origin of harmonic tonality . Kassel 1965.
6. ↑ Renate Imig: Systems of functional designation in the theory of harmony since Hugo Riemann . Düsseldorf 1970.
7. ↑ Guerino Mazzola : Geometry of Tones . Basel 1990, pp. 78, 110.