halftone

Diatonic intervals
Prime second third fourth fifth sixth seventh octave none decime undezime duodecime tredezime semitone / whole tone
Special intervals
Microinterval Comma Diësis Limma Apotome Ditone Tritone Wolf fifth Natural septime
units
Cent Millioctave Octave Savart

Halftone ( Latin semitonium even griech./lat. Hemitonium ) referred to in the music , the smallest interval of the current standard twelve- tone system . In exceptional cases, the designation is also applied to individual tones ( see below ).

Semitone as an interval

The interval designation halftone replaces the more complete designations halftone step or halftone spacing in a handy short form .

The music theory differs between the diatonic halftone (small second , z. B. g → as) and the chromatic halftone (excessive Prime , z. B. as → a), which together form a whole tone yield. The enharmonic semitone (double diminished third, e.g. f sharp → asas) is rarely mentioned.

Depending on the mood and musical context, the individual semitones are faintly audible.

Equal tempered semitone

In the equally tempered tone system , the semitone corresponds to one twelfth of the octave . This meaning was already anticipated by Aristoxenus by dividing the octave into six equal whole tones and defining the semitone as half of a whole tone.

The computationally exact twelfth division of the octave results in a frequency ratio (proportion) of cents for the tempered semitone , since this value multiplied twelve times by itself gives the frequency ratio of an octave (2/1). ${\ displaystyle {\ sqrt [{12}] {2}} {\ widehat {=}} {\ text {100}}}$

Semitones of the Pythagorean mood

In Pythagorean tone systems, due to the perfect fifths (proportion ³ ⁄ ₂ ), there is no "natural" semitone ( ¹⁶ ⁄ ₁₅ ) (coming from the lower range of the overtone series ), but the interval with the proportion cents , which Philolaos uses " Diesis ", in Euclid “ Leimma ”, which has also been called a semitone since late antiquity. ${\ displaystyle {\ frac {256} {243}} {\ widehat {\ approx}} \ {\ text {90}}}$

Without practical use, the apotome ( cent ) was also referred to as a semitone : the difference between a whole tone ( ⁹ ⁄ ₈ ) and Leimma ( ²⁵⁶ ⁄ ₂₄₃ ). The tone letters and the musical notation clearly distinguish these intervals: the leimma is a small second ch, the apotome a chromatic step, namely the excessive prime cis → c. ${\ displaystyle {\ frac {2187} {2048}} {\ widehat {\ approx}} \ {\ text {114}}}$

The difference is only canceled out by the equal tuning, as it makes the Pythagorean comma (= apotome-leimma) disappear and thus enables an enharmonic mix-up .

Small and large semitones of the harmonious, pure mood

The inclusion of the pure major third with the proportion ⁵ ⁄ ₄ in the pure tuning that has emerged since the Renaissance changed the order of magnitude of the semitones. The diatonic semitone , the large semitone with the proportion can now be assigned to the lower area of the overtone series. ${\ displaystyle {\ frac {16} {15}} {\ widehat {\ approx}} \ {\ text {112 cents}}}$

Because of the existence of two whole tones, there are also two chromatic semitones (excessive primes), the small semitones with the proportions and . ${\ displaystyle {\ frac {135} {128}} {\ widehat {\ approx}} \ {\ text {92 cents}}}$ ${\ displaystyle {\ frac {25} {24}} {\ widehat {\ approx}} \ {\ text {71 cents}}}$

Example:

Name of the tone	C.		, CIS		D.		,, DIS		, E
frequency	264		278.4		297		309.4		330
In cents (rounded)	0		92		204		275		386
Halftone in cents		92		112		71		112

Name of the tone	C.		'OF		D.		'IT		, E
frequency	264		281.6		297		316.8		330
In cents (rounded)	0		112		204		316		386
Halftone in cents		112		92		112		71

Fingering chart based on Peter Prelleur's The Art of Playing on the Violin (1730)

The following rule of thumb still applies to the intonations of a cappella listening (rule of the Weißenburg cantor Maternus Beringer, 1610).

“Semitones on the same line in the staff (the chromatic) are to be intoned as a small semitone ( semitonus minor ). Semitones on neighboring lines (the diatonic ones ) but as a large semitone ( semitonus major ). "

As can be seen in the frequency table and the fingering table by Peter Prelleur , the tones marked with a cross are CIS , DIS etc. lower than the DES , ES etc. marked with a b .

This harmonic intonation is in contrast to the expressive intonation , in which the leading tones ( C sharp leading tone to D , D flat to E , D flat to C , Eb to D and so on) are played more closely.

Music samples

Music example 1: Chords here after "Blessed are you" EKG Württemberg No. 651

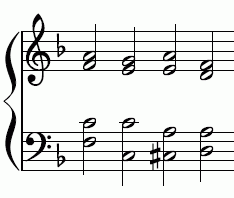
	pure mood medium tone mood equal mood

Tone step in the bass	in pure mood	in a mid-tone mood	in an equal mood
C-Cis	71 cents	76 cents	100 cents
C sharp-D	112 cents	112 cents	100 cents

Music example 2: Passus duriusculus . Chords here after WA Mozart “Misericordias Domini” in D minor (KV 205 a).

	The semitone steps in the bass are in the pure tuning	c → h: 112 cents h → b 92 cents b → a 112 cents a → as 71 cents as → g 112 cents

Table overview

At the end of the 19th century, the interval unit cents was defined as a hundredth of the semitone of the same level . It allows a particularly clear comparison of the sizes of the different halftones:

The semitones of the Pythagorean scale

{\ displaystyle C - {\ frac {9} {8}} - D - {\ frac {9} {8}} - E - {\ frac {256} {243}} - F - {\ frac {9} {8}} - G - {\ frac {9} {8}} - A - {\ frac {9} {8}} - H - {\ frac {256} {243}} - C}

or. …

{\ displaystyle A - {\ frac {256} {243}} - B - {\ frac {9} {8}} - C}

interval	Frequency ratio	in cents	example
Whole tone	⁹ ⁄ ₈	204 cents	CD
Halftone Leimma	²⁵⁶ ⁄ ₂₄₃	90 cents	EF
Halftone apotome	²¹⁸⁷ ⁄ ₂₀₄₈	114 cents	bra

The apotome is a purely arithmetical interval. In medieval music, the two notes B and B are never used at the same time.

The semitones of the pure scale

{\ displaystyle C - {\ frac {9} {8}} - D - {\ frac {10} {9}} -, E - {\ frac {16} {15}} - F - {\ frac {9 } {8}} - G - {\ frac {10} {9}} -, A - {\ frac {9} {8}} -, H - {\ frac {16} {15}} - C}

interval	Frequency ratio	in cents	example
large whole tone	⁹ ⁄ ₈	204 cents	CD
small whole tone	¹⁰ ⁄ ₉	182 cents	D-, E
diatonic semitone	¹⁶ ⁄ ₁₅	112 cents	, EF
large chromatic halftone	¹³⁵ ⁄ ₁₂₈	92 cents	C-, Cis
small chromatic halftone	²⁵ ⁄ ₂₄	71 cents	'BRA

The semitones of the 1/4 decimal point mean-tone scale

The frequency ratios are - except for the octave ( ² ⁄ ₁ ) and major third ( ⁵ ⁄ ₄ ) - irrational. Therefore the interval size is given in cents .

C - 193 cents - D - 193 cents - E - 117 cents - F - 193 cents - G - 193 cents - A - 193 cents - H - 117 cents - C

interval	Size in cents	example
Whole tone	193 cents	CD
diatonic semitone	117 cents	EF
chromatic halftone	76 cents	C-Cis

The semitones of the equal scale

C - 200 cents - D - 200 cents - E - 100 cents - F - 200 cents - G - 200 cents - A - 200 cents - H - 100 cents - C

interval	Size in cents	example
Whole tone	200 cents	CD
diatonic semitone	100 cents	EF
chromatic halftone	100 cents	C-Cis

Summary

interval	proportion	Size in cents
Twelfth part of the octave	${\ displaystyle {\ sqrt [{12}] {2}}}$	100 cents
Leimma	²⁵⁶ ⁄ ₂₄₃	≈90 cents
Apotomes	²¹⁸⁷ ⁄ ₂₀₄₈	≈114 cents
diatonic semitone	¹⁶ ⁄ ₁₅	≈112 cents
large chromatic halftone	¹³⁵ ⁄ ₁₂₈	≈92 cents
small chromatic halftone	²⁵ ⁄ ₂₄	≈71 cents
diatonic mid-tone semitone	${\ displaystyle {\ frac {8} {25}} {\ sqrt [{4}] {5 ^ {3}}}}$	≈117 cents
chromatic mid-tone semitone	${\ displaystyle {\ frac {5} {16}} {\ sqrt [{4}] {5 ^ {3}}}}$	≈76 cents
Vincenzo-Galilei halftone approximation	¹⁸ ⁄ ₁₇	≈99 cents

Chromatic scale

A twelve-step scale made up entirely of semitone steps is called a chromatic scale . The semitone steps are partly diatonic (small seconds) and partly chromatic (excessive prime). Chromatic semitones are on the same line, diatonic semitones are on adjacent lines.

Audio samples

Semitone up C-D flat ^?^/ⁱ
Semitone down CH ^?^/ⁱ

Halftone as a single tone

Occasionally the term semitone is used to refer to single tones.

In Carl Eitz's tone word method , the term semitone is used for a single level of the chromatic scale, while the root tones are called whole tones . In the context of this expression, the whole tones form a subset of the entire set of semitones.

In the past, the original tones (white keys on the keyboard) were sometimes (in a way that is unusual today ) called whole tones and their chromatic variants (black keys on the keyboard) as semitones. Johann Sebastian Bach obviously aims at this meaning when he speaks of “Præludia and Fugues through all Tones and Semitonia” on the title page of his Well-Tempered Clavier . Piano builders still use this language today (2018).

Web links

Wiktionary: Halftone - explanations of meanings, word origins, synonyms, translations

Individual evidence

↑ This semitone step results as a fourth - 2 whole tones . The frequency ratio is calculated as ⁴ ⁄ ₃ × ⁸ ⁄ ₉ × ⁸ ⁄ ₉ = ²⁵⁶ ⁄ ₂₄₃ (see Pythagorean tuning ).
↑ In Euler notation . Example: 'CIS ("low point CIS") or' DES ("single point DES") means: The CIS or DES in the Pythagorean circle of fifths is increased or decreased by a syntonic comma.
↑ This rule was formulated in many ancient singing schools. Here after Maternus Beringer: Musicae, that is the free, lovely art of singing . Georg Leopold Fuhrmann, Nuremberg 1610 (reprint: Bärenreiter, Kassel 1974).

[1] This semitone step results as a fourth - 2 whole tones . The frequency ratio is calculated as ⁴ ⁄ ₃ × ⁸ ⁄ ₉ × ⁸ ⁄ ₉ = ²⁵⁶ ⁄ ₂₄₃ (see Pythagorean tuning ).

[2] In Euler notation . Example: 'CIS ("low point CIS") or' DES ("single point DES") means: The CIS or DES in the Pythagorean circle of fifths is increased or decreased by a syntonic comma.

[3] This rule was formulated in many ancient singing schools. Here after Maternus Beringer: Musicae, that is the free, lovely art of singing . Georg Leopold Fuhrmann, Nuremberg 1610 (reprint: Bärenreiter, Kassel 1974).