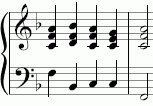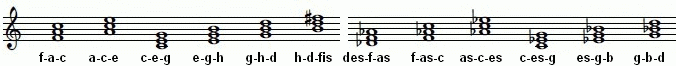Pure mood
As pure mood a musical will sound system referred to, wherein in the diatonic scales the tone levels octave , fifth , fourth and major third frequency ratios of exactly 2: 4 have the tonic: 1, 3: 2, 4: 3 and 5 respectively.
This requires subtle deviations from today's common mood . Many musical instruments and singers can realize these deviations; the better this succeeds, the more perfect the harmony is felt. This is based on the fact that in natural sounds, in addition to the fundamental tone, overtones, whose frequency is an integral multiple of the frequency of the fundamental tone, also resonate. If these partially coincide in the case of chords, the sound is perceived as harmonic; if the chords are out of tune the sound becomes rough.
In the Pythagorean tuning of the Middle Ages, only the octaves, fifths and fourths were in tune .
Regardless of the mood, the word pure in the intervals prime, fourth, fifth and octave is also used simply as the opposite of diminished or excessive .
history
Pure tuning arose in Western Europe with the advent of polyphony in the second half of the 15th century. Its use was first mentioned by Walter Odington , who mentions the major third as a consonant. The ars subtilior integrated the major third into a newly emerging triad conception until Bartolomé Ramos de Pareja expanded this way of thinking theoretically for the monochord in a musical treatise from 1482. Through Lodovico Foglianos' work "Musica Theorica" from 1529 the pure tuning became better known.
use
In polyphonic music, the ideal of pure tuning is widespread in vocal ensembles, choirs and ensembles with wind and string instruments. Listening to each other enables pure chords to sound. In choir schools, for example, the correct intonation is explained using the theory of pure tuning.
A special feature of making music in pure tuning is that with modulations , not only tones change by changing the sign, but also a further tone by a syntonic comma . For example, compared to C major, G major requires the tone F sharp instead of the tone F and also the tone A higher by a syntonic comma (see modulations in pure tuning ). That is why a tuning for several keys can only be achieved with keyboard instruments if there are more than 12 keys per octave, as is the case with the Archicembalo . Such instruments are practically unplayable and could not gain acceptance. On keyboard instruments with 12 fixed pitches per octave, if several or even all scales of the circle of fifths are to be usable, a deviation from the ideal of pure tuning, tempering is necessary. Losses in the melodious sound of chords have to be accepted (see also pure tuning for keyboard instruments ).
The mid-tone tuning in the 16th to 18th centuries contains purely tuned major thirds. This is achieved by making fifths more closely tuned.
Example of four mean-tone fifths and the corresponding pure third Four-point- mean-tone fifths and a pure third (a '= 440 Hz)
The mean-tone tunings have the limitation that not all keys can be played. Only the well-tempered tunings and the equally tempered tuning allow playing in all keys, but move away from the ideal of pure tuning by sharpening the pure third. (The fifths are improved compared to the mid-tone tuning.)
Not only in the Western musical tradition, but also in non-European musical cultures, one often encounters harmoniously pure intonations . In individual cases, other intervals of the overtone series are also included, such as the natural seventh (7th partial ) or the Alphorn Fa (11th partial).
Keys in pure tuning
Purely tuned keys play a decisive role in the performance practice of the music of the Renaissance and Baroque periods by a cappella choirs, string quartets or orchestras. With pure intonation, a clear basic tone feel (because of the difference tones ) and a beat-free sound (because of common overtones ) is achieved. This of course also applies to the music of the Classical and Romantic periods and is ideally aimed at in their brass sections. At the same time, however, the intonation becomes more complicated due to the expansion of chordal possibilities away from the simple triads to an extreme chromatization of the movement, for example in Richard Wagner's .
| A major cadence |
purely
(No beats.) |
|---|
Since only one key can be played on keyboards with 12 keys, the spacing of the circle of fifths has been slightly changed. With the mid-tone tuning so that the thirds sounded in pure form. Many keys - though not all - could be played that way. In the case of equal tuning, so that the octave is divided into 12 equal semitones. Here the thirds sound rough.
|
mid-tone
(Low beats, caused by the |
equal
(Violent beats - about ten times |
Octave, fifth and major third form the basic intervals of the pure tuning. All further intervals can be put together from these basic intervals. This is why this system is also called the fifth-third system .
Frequency ratios of the major and minor scales in pure tuning
Pure scales are based on the following frequency relationships:
C major (as an example) C. D. E. F. G A. H c Interval
frequency ratio to the fundamentalPrime
1 / 1large second
9 / 8large third
5 / 4Fourth
4 / 3Fifth
3 / 2large sixth
5 / 3large seventh
15 / 8Octave
2 / 1Frequency ratio of neighboring tones 9 / 8 10 / 9 16 / 15 9 / 8 10 / 9 9 / 8 16 / 15 C minor (as an example) C. D. It F. G As B. c Interval
frequency ratio to the fundamentalPrime
1 / 1major second
9 / 8minor third
6 / 5Fourth
4 / 3Fifth
3 / 2minor sixth
8 / 5minor seventh
9 / 5Octave
2 / 1Frequency ratio of neighboring tones 9 / 8 16 / 15 10 / 9 9 / 8 16 / 15 9 / 8 10 / 9
The chords of the tonic CEG or C-Es-G, the subdominant FAc or F-As-c and the dominant GHd or GBd (in minor) consist of perfect fifths and thirds. The fifth DA, however, is impure. A chord on the second level therefore already means an (intermediate) modulation towards the subdominant . In the scales in just intonation is to be noted that there are two types of whole tones, for example, C to D with the frequency ratio 9 / 8 and D to E to the frequency ratio 10 / 9 .
As a result, these scales deviate unmistakably from the scale in equal tuning, in which every semitone makes up exactly one twelfth of the octave and a whole tone corresponds to exactly two semitones.
The additive notation of the major and minor scales
Main article: The division of the octave into 53 pitches
At the time of Zarlino (1517–1590) it was taught in music schools that parts can be assigned to intervals:
- large whole tone = 9 parts
- small whole tone = 8 parts
- diatonic semitone = 5 parts
If you note the distance of the scale from c (in brackets) or from the adjacent tone (set lower) in this division, you get:
C-Dur: c(0) 9 d(9) 8 e(17) 5 f(22) 9 g(31) 8 a(39) 9 h(48) 5 c(53) c-moll: c(0) 9 d(9) 5 es(14) 8 f(22) 9 g(31) 5 as(36) 9 b(45) 8 c(53)
The chromatic semitone (from es to e, as to a and b to h) results in 3 parts.
Since the octave constitutes 53 parts, one part is 1 / 53 of the octave = 1 / 53 • 1200 cents = 22.6 cents.
- Major third (approximate value) = interval ce = 17 parts = 384.9 cents (exactly: 200 • log 2 (5/4) = 386.3 cents)
- 5th (approximate value) = interval cg = 31 parts = 701.9 cents (exactly 1200 • log 2 (3/2) = 701.0 cents)
The deviations of the approximate values here from the exact values are smaller than a schism (2 cents) and thus at the limit of the perceptible tone difference.
The major third
Basically, the characteristic pure third with the frequency ratio 5 / 4 . The mid-tone tuning with its many pure thirds almost completely realized the pure tuning for keyboard instruments - but only for a limited number of keys.
The pure major third was first mentioned around 1300 by Walter Odington in his De Speculatione Musices . Earlier descriptions of this interval are related to the ancient Greek tone system .

|
Purely: mid-tone: Pythagorean: equal: | The pure third with the frequency ratio 5 / 4 was now (in contrast to the Pythagorean third with the frequency ratio 81 / 64 felt) as a consonance. It took several centuries for the third (similar to the Pythagorean third) to be accepted.
In pure and mid-tone tuning, the pure third (386 cents) does not beating. In the mid-tone tuning you can hear the slightly tempered fifth in the second chord in a slight beat. The “sharpened” third in equal (400 cents) or even Pythagorean (408 cents) tuning with a strong beat is felt as friction. (See also the example of the major third with a reinforced difference tone .) |
Note: Pure intervals are characterized by integer frequency ratios, while tempered intervals usually have an irrational frequency ratio. Therefore the size comparison is made with the unit cent .
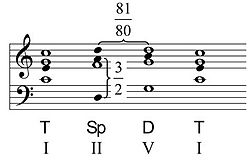
The second degree chord
The pure tuning of the C major scale with the D of the dominant chord GHD and the A of the subdominant chord FAC results in a fifth DA , which is a syntonic comma too narrow and thus appears dissonant .
The second level chord is an intermediate modulation towards the subdominant . The D of A minor (or F major) results in a pure minor chord DFA . In the following cadence, the D in the second degree Sp chord is a syntonic comma lower than in the D chord of the dominant.
If this is not observed, the mood of a choir can drop. (see "Comma trap".)
However, the second degree chord can also be interpreted as a double dominant - often discussed less often in the literature - as D-F sharp-A. In this case - modulation towards the dominant - the A is increased by a syntonic comma.
Mathematical description
The interval space of the pure tuning is the fifth-third system .
All intervals can be represented as multiples of the three basic intervals Ok (octave), Q (fifth) and T (major third).
| interval | presentation | Frequency ratio |
|---|---|---|
| octave | Ok (basic interval) | 2: 1 |
| Fifth | Q (basic interval) | 3: 2 |
| Major third | T (basic interval) | 5: 4 |
| Fourth | Ok - Q | 4: 3 |
| Small sixth | Ok - T | 8: 5 |
| Minor third | Q - T | 6: 5 |
| Major sixth | Ok + T - Q | 5: 3 |
| (Big) whole tone | 2Q - Ok | 9: 8 |
| Small whole tone | T - (large whole tone) = Ok + T - 2Q | 10: 9 |
| Minor seventh (1st possibility) | Ok - (large whole tone) = 2Ok - 2Q | 16: 9 |
| Minor seventh (2nd possibility) | Ok - (small whole tone) = 2Q - T | 9: 5 |
| halftone | Fourth - T = Ok - Q - T | 16:15 |
| Major seventh | Ok - semitone = Q + T | 15: 8 |
| Syntonic comma | 2 (large whole tones) - T = 4Q - 2Ok - T | 81:80 |
| detailed table | ||
Problems with keyboard instruments
With modulations, tones change not only by a semitone, but also some tones by a syntonic comma (see modulation for pure tuning ). This cannot be achieved on a keyboard with twelve notes per octave. One was forced to use tempered moods. First:
- the mid-tone moods , then
- the well-tempered moods and finally
- the equal mood .
Modulations require the pitch to be adjusted
- Rule of thumb: When modulating into a neighboring key, two tones change, one of which is recognizable with a change in sign, the other slightly by a syntonic comma . (Frequency ratio 81 / 80 21.5 cents. This is about 1 / 5 semitone.)
For example, when modulating from C major to F major, not only does the B decrease by a semitone to B , but also the D by a syntonic comma . At a modulation of C minor to F minor, the reduced B a syntonic comma and the D by a semitone to Des .
Accordingly, when modulating from C major to G major, not only does the F increase by a semitone to F sharp , but also the A by a syntonic comma. At a modulation of C minor to G minor, the increase F by one syntonic comma and the As a semitone to A .
Comparison of the expanded pure tuning with the equal tuning
If you add the F sharp of G major and the D flat of F minor to the notes of the C major and minor scales, you get the 12-step chromatic scale of pure tuning.
Chromatic scale of the pure tuning of C major and C minor supplemented by F sharp and D flat:
Note: When comparing intervals, the unit cents is used . The following applies: 1 octave = 1200 cents.
Name of the tone C. Of D. It E. F. F sharp G As A. B. H c frequency 264 281.6 297 316.8 330 352 371.25 396 422.4 440 475.2 495 528 In cents 0 112 204 316 386 498 590 702 814 884 1018 1088 1200
The following triads contain perfect fifths and pure minor and major thirds.
In this tuning you can only play C major and C minor as well as A major and E minor (with the minor dominant HD-F sharp). (If the D flat in the major dominant chord B-D flat-F sharp is replaced by its enharmonic mix-up of E minor, the result is an E flat that is 41 cents too high.) In order to be able to play in all keys, in the case of the equal Tuning the semitones adjusted. It is accepted as a compromise that there is no longer a pure triad.
Equal tuning chromatic scale:
Name of the tone C. Cis / Db D. Dis / Es E. F. F sharp / Ges G G sharp / a flat A. Ais / B H c frequency 261.6 277.2 293.7 311.1 329.6 349.2 370 392 415.3 440 466.2 493.9 523.3 In cents 0 100 200 300 400 500 600 700 800 900 1000 1100 1200
The equal tuning can also be obtained by distributing the Pythagorean comma in the circle of fifths FCGDAEH-Fis-Cis-Gis-Dis-Ais-Eis-His = (C?) Over the twelve fifths. The perfect fifth (702 cents) differs only slightly from the equivalent (700 cents). The major third (386 cents) is "sharpened" by 14 cents in the equal tuning (400 cents).
Frequency ratios of the expanded scale
If you add the F sharp of G major (dominant) and the D flat of F minor (subdominant) to the C major and C minor scales , you get twelve levels.
C major / C minor chromatic C. Of D. It E. F. F sharp G As A. B. H c Frequency ratio to the fundamental 1 / 1 16 / 15 9 / 8 6 / 5 5 / 4 4 / 3 45 / 32 3 / 2 8 / 5 5 / 3 9 / 5 ( 16 / 9 ) 15 / 8 2 / 1 Frequency ratio of neighboring tones 16 / 15 135 / 128 16 / 15 25 / 24 16 / 15 135 / 128 16 / 15 16 / 15 25 / 24 27 / 25 ( 16 / 15 ) 25 / 24 ( 135 / 128 ) 16 / 15 in cents 112 92 112 71 112 92 112 112 71 133 (112) 71 (92) 112
Here the B is chosen as a pure minor third to G (belonging to C minor). In some representations (emphasizing fifths) the B is chosen as a fourth to F (given in brackets) with the advantage that the interval AB is a diatonic semitone. But then this B already belongs to F major.
As you can see, an instrument tuned in this tuning can only be used for C major and C minor (with a suitable B flat) as well as A flat major and E minor and is practically not realized.
Small and large halftone
In the pure tuning there is the large, the diatonic semitone with the frequency ratio and the small, the chromatic semitone with the frequency ratio and
In the chromatically extended C major / C minor scale:
- Diatonic halftones at 112 cents: E → F and H → c , and C → Des , Cis → D , D → It and Dis → E .
- Chromatic semitones with 92 cent: C → C sharp and Des → D .
- Chromatic semitones with 71 Cent: D → Dis and it → E .
- (Note: C → D is a large whole tone with 204 cents and D → E is a small whole tone with 182 cents. Therefore, the two chromatic semitones differ by 21 cents.)
Euler's notation
The two most important intervals in triad formation are the fifth and the third. Since the purely tuned third does not appear in the circle of fifths, Euler developed a precise notation that enables a precise definition of the pitch that is hidden in the musical notation.
- ... -bfcgdae ... (fifths with the frequency ratio 3: 2)
- ... -, b-, f-, c-, g-, d-, a-, e ... The tones "low point b", "low point f" ... are a syntonic comma lower than in the first row.
- Conclusion: The intervals c-, e and d-, f sharp and e-, g sharp and f-, a and g-, h etc. have the frequency ratio 5: 4.
This notation was used by various music theorists such as Moritz Hauptmann , Hermann von Helmholtz and Arthur v. Oettingen used and led to new musical instruments such as the pure harmonium .
The pure scales always have the same representation in this representation: The third, sixth and seventh notes of the scale are a syntonic comma lower in major, and a syntonic comma higher in minor.
| F major | f | G | , a | b | c | , d | , e | f | , D minor | , d | , e | f | ,G | , a | b | c | , d |
| C major | c | d | , e | f | G | , a | ,H | c | ,A minor | , a | ,H | c | , d | , e | f | G | , a |
| G major | G | a | ,H | c | d | , e | , fis | G | , E minor | , e | , fis | G | , a | ,H | c | d | , e |
You can see immediately that with modulations, individual tones change by a syntonic comma. For example at the transition
- from C major to G major the tone, a to a,
- from C major to F major or, A minor, the tone d to, d.
The calculation of the corresponding cent values with octave = 1200 cents, fifth = 701.955 cents and syntonic comma = 21.506 cents results, for example, with c = 0 cents rounded:
- e = c + 4 fifths - 2 octaves = 408 cents and, e = e - syntonic comma = 386 cents (= c + pure major third)
The corresponding frequency values are calculated with c = 264 Hz as follows:
- and .
Sound example: comparison of pure, mid-tone and equal tuning
Sentence Friedrich Silcher
| Listen | |||
| Pure mood | Pure mood slowly | 1/4 point mean tone tuning | equal mood |
|---|---|---|---|
|
1st line:
2nd line: |
1st line slowly:
2nd line slowly: |
1st line:
2nd line: |
1st line:
2nd line: |
Here the cadenza chords (in Euler notation) G-'BD, C-'Es-G and D-, F sharp-A are in pure tuning in G minor. When modulating to 'B flat major (measure 6 and measure 13) with the pure cadence chords' BD-'F,' Es-G-'B and 'FA-'C, the note C increases by a syntonic comma to' C. .
More sound samples
For the tonal representation of pure moods, a well-known, although historically incorrect example was chosen, which makes it possible to clearly hear the difficult differences. It was designed by Johann Sebastian Bach for one of the (many) well-tempered tunings ; Exactly for which one can no longer be reconstructed with certainty today.
Johann Sebastian Bach: Prelude in C major from the first volume of the Well-Tempered Clavier , BWV 846
Example 1 : bars 1 to 5
- The 7-stage described in the text (pure) C-major scale, although resulting in a melodic meaningful large whole tone ( 9 / 8 ) cd [wherein a)], but the fifth is that [in b)] defiled ( 40 / 27 instead of 3 / 2 ; it has about 680.448 cents a syntonic comma too) small.
- The fifth is by expanding the scale to a degraded d [wherein a)] as well, although adjusted [with b)], but is formed on the one hand a unmelodic smaller whole tone ( 10 / 9 ) and on the other a distinctly audible (syntonic) point difference ( 81 / 80 ) between the d's of the second and third clock [wherein c)].
- Upon acceptance of the natural seventh ( 7 / 4 instead of 9 / 5 ) in the dominant [wherein d)] is produced an additional "septimales comma" ( 64 / 63 , about 27.264 cents) f between the second and third clock [e) ]. The Gleitton fe is called "septimaler halftone" ( 21 / 20 , about 84.467 cents) closely intonation [wherein f)].
Example 2 : bars 5 to 11
- Also, the 12-stage chromatic scale contains (only) the impure fifth as ( 40 / 27 ), the twice here as part of the double Dominant sounds -Septakkordes [wherein a)].
- The compensation of this fifth now requires a Pythagorean eingestimmtes a ( 27 / 16 instead of 5 / 3 ), which compared with the a and root of the tonic parallel is increased by a comma syntonic [with b)]. Since the point differences are heard in one of the middle voices, they are hardly significant - with a thoroughly acceptable tonal result.
- In contrast to this, the tone c of the double dominant, intoned as a natural seventh, leads to the clearly audible “septimal comma” [in c)].
literature
- Hermann von Helmholtz : The theory of tone sensations as a physiological basis for the theory of music . Vieweg, Braunschweig 1863 (reprint: Minerva-Verlag, Frankfurt am Main 1981, ISBN 3-8102-0715-2 , excerpt ).
- Ludwig Riemann: Popular representation of acoustics in relation to music. Following Hermann von Helmholtz's "Theory of Sound Sensations". Vieweg, Braunschweig 1896.
- Albert Limbach: The art of pure intonation. Studies on unaccompanied solo and choral singing in opera and concert. Breitkopf and Härtel, Wiesbaden 1980, ISBN 3-7651-0168-0 .
- Bettina Gratzki: The pure intonation in choral singing (= Orpheus series on basic issues in music 70). Publishing house for systematic musicology GmbH, Bonn 1993, ISBN 3-922626-70-X ( excerpt ).
- Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You Should Care). WW Norton & Company , New York NY 2007, ISBN 978-0-393-06227-4 ( excerpt ).
- Adrian Wehlte: Trios for two (trio with 2 flutes and combination tone , explanations and exercises for pure tuning) Tibia Heft 2/2012 Moeck-Verlag , Celle 2012, ISSN 0176-6511 and practice booklet .
Web links
- “The pure mood” by Joachim Mohr
- Just Intonation - Free software that allows you to play and hear music in tune, regardless of the key
- Early Music Sources: Just intonation in the Renaissance on YouTube (English, with German subtitles)
See also
- Solmization
- Tonic sol-fa , there also the report by Hermann von Helmholtz, an advocate of pure tuning
- Barbershop (music) , there pure mood as an essential characteristic of this modern music genre
- Mid-tone mood
- Well-tempered mood
- Equal mood
- Circle of fifths
swell
- ↑ The pure tuning can lead to conflicts with an accompanying piano etc. The cellist Pablo Casals wrote in The Way They Play (1972): Don't be alarmed if you have a different intonation than the piano. It's because of the piano, which is out of tune. The piano with its equal tuning is a compromise in intonation .
- ↑ The music in past and present 1986 vol. 13 p. 217 "Temperatur und Mood"
- ↑ The music in past and present 1986 vol. 13 p. 544 "Tonsysteme"
- ↑ Bettina Gratzki: The pure intonation in choral singing p. 25
- ↑ Johann Philipp Kirnberger , Mixed Music 1769 pp. 26-27 and Flute Sonata in G major Adagio
- ↑ s: en: Catholic Encyclopedia (1913) / Walter Odington
- ^ The Harvard dictionary of music, Don Michael Randel, 2003, ISBN 0-674-01163-5 , page 56, heading: Arithmetic and harmonic mean, section 2 online
- ↑ History of Music: The First Times of the New Christian World and Art. The development of polyphonic singing. 1864. Vol. 3. During the Renaissance, up to Palestrina. 1868, History of Music: Volume 2, Wilhelm Bäumker, 1864, page 361 online
- ↑ In Euler's notation, the C major scale is cd, efg, a, h c. The fifth d, a and the second degree chord df, a are impure. If you decrease d by a coming after, d (modulation in subdominant direction), the fifth, d, a and the minor chord, df, a become pure.
- ↑ Lesson: The 2nd degree chord, the comma trap, the Neapolitan sixth chord and the double dominant . kilchb.de. Retrieved October 4, 2019.
- ↑ A 12-point scale of pure tuning is purely theoretical and therefore arbitrary. Here, for example, the B of the pure G minor chord is used. One could just as justifiably choose - and this is how it is often seen - the B as a perfect fifth to F.
- ↑ Arnold Schönberg describes the theory of harmony in his music theory . (Vienna, 1911; third edition 1922) the pure tuning, whereby he assigns the tritone (F sharp) to the middle of the octave (equally floating).
-
↑ In the notation of Euler's Tone Network , the chromatic scale is described as follows, with a distance from c in cents:
- c 0 | 'of 111.73 | d 203.91 | 'it 315,64 | , e 386.31 | f 498.04 | , fis 590.22 | g 701.96 | 'as 813.69 | , a 884.36 | 'b 1017.60 (b 996.09) | , h 1088.27 | c 1200
- ↑ The term small or chromatic semitone has thus become common. Strictly speaking, it is an excessive prim.
- ↑ The rhythmic version in three meter was replaced by an isometric version as early as the 18th century. See: http://www.liederlexikon.de/lieder/wer_nur_den_lieben_gott_laesst_walten
- ↑ Note in Euler notation is a major triad of the form x-, yz or 'xy-'z, a minor triad of the form x-'yz or, xy-, z.