Music theory in ancient Greece

from Wikipedia, the free encyclopedia

The music theory in ancient Greece was highly developed. Efforts have already been made to formulate a tone system , use differentiated notation of the pitches and extensive discussions about possible ethical and character content of music and making music. The theorists of the West , in the early Middle Ages as well as again in the Renaissance , took ancient Greek music theory as their starting point. Severinus Boethius, for example, is considered to be the messenger of ancient musical conceptions for the early Middle Ages; in the Renaissance, especially the newly discovered was Aristotle - Reception also with regard to the impetus of the music looked back at the idealized ancient times to turn.

Basic concepts

"Harmony", "Symphonia", "Consonance" and "Scale" have always been central terms in music theory . These terms were essentially coined in the music theory of ancient Greece, and became the central terminology in the development of Western music theory, especially since its beginnings in the Middle Ages . Their meanings in antiquity were:

  • The first consonances were: the octave (1: 2), the fifth (2: 3) and the fourth (3: 4) as well as the octave plus fifth or fourth. The grading of the consonance qualities happens in exactly this order. Consonance was expressed with symphonia = "sounding together" and thus means the simultaneous sounding of tones in the corresponding vibration relationships. All other intervals were designated with diaphonia = "sounding apart" and apparently regarded as dissonant , which in no case means that they were hardly used or not at all: They provided the main tone steps for the harmonia , the melody. Harmonia did not, like our concept of 'harmony', describe the vertical, but the horizontal tone structure. There was very probably no polyphony in the true sense of the word . Several singers or instrumentalists played either in unison or in octave parallels.
  • Scales were shown in descending order. It is sometimes assumed that descending tone sequences were perceived as more pleasant.
  • The tetrachord was the first sound ordering principle . A tetrachord ( ancient Greek for "four-string" or "fourth tone") is a four-tone sequence in the interval of a fourth . The basic tetrachord had the structure whole tone - whole tone - semitone (1 - 1 - ½); z. B. a - g - f - e. This structure probably stems from the number of strings and the tuning of the Phorminx, which is considered the oldest known stringed instrument of the Greeks. In ancient Greek music theory, the tetrachord was the primary structure for the order of tones and the formation of octave genres or keys ( tónoi ). The decisive factor is the sequence of the tone steps, which are read in descending order: The tetrachord depicted is a Doric (or hypodoric) one.
    Hypodoric tetrachord: agfe     play ? / i .Audio file / audio sample
    Attention : Medieval music theory used the ancient terminology for the so-called church modes, but was probably subject to a translation error. In the system of church tones, the tetrachord shown was a Phrygian (to be read in ascending order: efga; i.e. semitone-whole-tone-whole tone).
  • Second tone ordering principle were the keys ( tonoi ). Starting from one tone level of the tone system, the Systema Teléion (from a1 down to b; see section below), as the basic tone, they form seven-step scales that combine parts of different tetrachords. Thus we have scales of different intervals and consequently of different characters. There was also the option of transposing the structure of a key to a different pitch (different keynote). The theorists give differently large sets of possible transposition scales ( trópoi ).
  • The third tone ordering principle was the tone gender . They are divided into diatonic, chromatic and enharmonic. Tone gender refers to variability within a tetrachord. So they are not to be confused with our current concept of tone gender.

The sound system

The tone system of ancient Greece was summarized as Systema Téleion ("large, complete system"). It shows and arranges the basic sound stock. Its development extended approximately from the 5th to the 3rd century BC. And by then had developed from a pentatonic to a heptatonic system. In summary, it was first presented in the text "Teilung des Canon " ("Katatomé Kanonos", Latin: "Sectio canonis"), which is ascribed to Euclid of Alexandria , but whose actual authorship is not certain. At around the same time (late 4th century BC) there are also descriptions of Aristoxenus BC. Taranto , which are only available in fragments or as a result of the tradition of later authors. Various scales could be formed
within the Systema Téleion . Furthermore, these could also be designed variably by the player and / or singer. For this, the Greeks knew three clay sexes . The tetrachords were put together in the Systema Teleion to form a double octave structure, which formed the basic diatonic scale.
The central octave was the scale e'-e, which was called Doric. It was considered to be best suited for singing and making music. It consists of two identically built tetrachords with the structure whole tone – whole tone – semitone (1-1-½; edch / agfe). It is essential here that scales and tetrachords were conceived and represented in descending order, whereas we have been used exclusively to ascending scales since the European Middle Ages . Theorists like Archytas of Taranto assumed a step smaller than the semitone for the last step of each tetrachord.
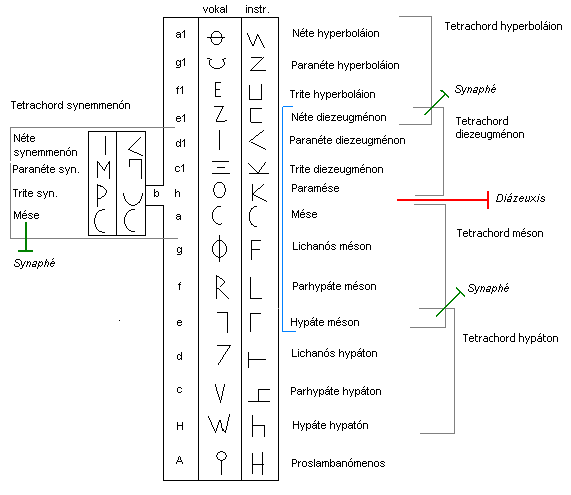
Representation of the Systema Téleion :

Depiction of the ancient Greek tone system

The illustration shows the descending double octave system with the corresponding pitches of the vowel and instrumental notation (see below Greek musical notation ). In the left column the modern tone names are added for orientation (Attention: The use of the modern tone names is only intended to make the interval structure of the Systema Téleion understandable. They do not serve as a direct translation of the Greek pitch names ). The blue bracket frames the area of ​​the central octave.
The octaves are made up of two tetrachords (1 - 1 - ½) of the same construction, which overlap with a common tone ( synaphé ).
The continuation of this tetrachord structure comes up against a limit at the position of the paramése : it should actually be the synaphé (the common tone) of the tetrachords diezeugménon and méson . This would mean that the tetrachord méson would consist of three whole steps (hagf) and consequently fall out of the system. The two tetrachords cannot overlap, but are separated by a diázeuxis (= "separation") at the Paramése and Mése levels . The tetrachord diezeugménon is the "separated".
In order to bridge this critical area, the system envisaged a possible shift of the Néte by one step, with which a tetrachord synemmenón (= "connecting") could be formed (see left in the illustration; d1-c1- b -a).
The application of the tetrachord synemmenón caused a "modulation". Therefore the Systema Téleion could also be called the “modulatable” ( Systema Metabolon ). Since the basic form, i.e. the system, was again considered to be unchangeable, the name Systema Ametabolon was also used.

The Systema Téleion shows us that the Greeks strove for a closed system. The last (lowest) note no longer finds a tetrachord, but is necessary to add to the octave. He is the Proslambanomenós - the "added one".

Basically it should be noted that the Systema Téleion "only" formed the basic tone system that a material scale made available. Practical music practice selected from this material and was thus familiar with various tetrachord structures and octave genres , which formed the tonoi (keys) and thus useful guides . By way of comparison: our modern western tone system also has a material scale which, based on the predominantly usual well-tempered equal-scale tuning , has twelve tones ready. While z. B. cover material and usage manager in twelve-tone music, the major / minor system only uses a certain selection from the twelve-tone reserve. Associated with a typical interval structure , a piece of music or a passage in a piece is clearly identified as e.g. B. C major or C minor recognizable.

Pitch names

The names of the pitches are:

  • Néte - (Νήτη) "the lowest"
  • Paranéte - (παρανήτη) "the next to the lowest"
  • Trite - (τρίτη) "the third"
  • Mése - (Μέση) "the middle one"
  • Paramése (Παραμέση) - "the one next to the middle one"
  • Lichanós - (Λιχανός) "the index finger"
  • Hypáte - (Ὑπάτη) "the colonel "
  • Parhypáte - (Παρυπάτη) "those next to the colonel"

The naming of the pitches probably comes from the string instrument ( Phorminx , Kithara or Lyra ). The order according to finger or string positions is clear: The highest sounding string is “the lowest”, the lowest sounding “the highest”. Some of the names of the pitches are also mythological borrowings. So in the case of the Néte , as a name for one of the muses .
It is important that these are pitches and not absolute pitches. Depending on the key (or mood) z. B. the Mése elsewhere.
Since the ancient Greek tone system had developed from a pentatonic to a heptatonic , the number of strings on the stringed instruments and the number of tones to be named also increased. The original strings of the Phorminx or Lyra were the Néte , Trite and Mése . In the end there were up to seven strings (as shown above; Lichanos is not a string, but refers to the grasping finger).
The basic tetrachords of the Systema Téleion are named after the tone levels: The tetrachord méson has the mése as the first level.

Greek musical notation

The Greeks had two types of notation: one for instrumental playing and one for vowel notation for singing. The notation symbols are letters that are used in the basic row in an authentic form and to cover the entire sound supply, sometimes with small strokes, folded over or turned upside down.
In the case of vowel notation, the notation symbols were placed above the text. Rhythm was only notated in fragments, using length or abbreviations. Basically, however, probably the considered meter or meter of each text as rhythmic orientation.

The vowel notation

The character set of the vowel notation is composed of the letters of the Greek ( Ionic ) alphabet. The core of the notation character set can be found in the octave f'-f. The signs of the tones outside this range are sometimes provided with small lines (lower tones), appear upside down or are additional, invented symbols. The area in brackets in the illustration frames the tone area as provided by the tone system, the Systema Téleion.

Vowel notation characters

The character set provides three rows:

  • The characters in the first row indicate the tones of the diatonic ladder as reproduced on the staff shown.
  • In the 2nd row there are the characters that indicate the upper tone of a semitone step. Example of the semitone step f'-e ': The tone f' is denoted by the character of the 2nd row, which is above that of the 1st row for the tone e '; so: f'-e '= EZ . (The characters for c and f, although tones of the diatonic ladder, are in principle taken from the 2nd row if they are the upper tone of a semitone step.)
  • The 3rd row shows the set of symbols for the tones which do not belong to the diatonic ladder and which mark a whole step above the tone below.

Example of the whole step c sharp'-b: For the c sharp ', as a non-diatonic tone, the character of the 3rd row is chosen, which is at the position of the diatonic c'; so: c sharp'-h = KO .

The Paian des Athenaois was established in 128 BC. In honor of Apollo in Delphi . Compared to other documents of ancient music, it has been preserved almost completely. The text and the vowel notation characters above were carved into a stone slab. The following translation into modern notes shows very nicely the use of the tetrachord synemmenón with the note symbol Λ in the last line: Here the previously used tetrachord g 'f' es' d 'is replaced by the synemmenón phrase f' es' des' c '.

Paian Athenian Treasure House Delphi, 1st part

The ancient Greek text goes something like this:

Hear me, you who own the deep forest of Elikona, you fortunate daughters of the great Zeus! To deceive with your words, fly your brother Phoebus with the golden hair, from the twin peaks of the rock Parnassus, accompanied by the splendid Delphic Virgins, his journey begins to the crystal waters of Castalia, crossing the Cape of Delphi, the prophetic mountain .

The instrumental notation

The symbols of the instrumental notation are composed of the letters of the Old Doric or Phoenician alphabet. The instrumental script is therefore much older than the vowel script; its origins go back to the 6th century BC. BC back. The three rows of characters make it clear that the notation is intended from the string instrument (the kithara). The tones that deviate from the diatonic system are predominantly indicated by variants of the core characters (mirroring or shifting), which most likely means the shortening of the string length (tone increase) by slightly sliding the grasping finger or using the second grasping finger.

Instrumental notation characters

The three rows of instrumental notation:

  • The characters in the first row indicate the tones of the diatonic ladder as reproduced on the staff shown.
  • In the 2nd row there are the characters that indicate slight increases in pitch (shortened strings) (maximum one semitone step). In the enharmonic tone sex, however, it can also be an increase of about a quarter tone.
  • The 3rd row shows the set of symbols for the tones which do not belong to the diatonic ladder and which mark a whole step above the tone below.

The tone sexes

As already seen above, the basic structure of the ancient Greek tone system was divided into diatonic tetrachords, which encompass the range of a pure fourth (3: 4) and as an inner structure the descending sequence of two whole steps and a semitone step (1 - 1 - ½) show.
However, the music-making practice provided for modifications of these tetrachords, which were included in the theory but not systematized. A distinction was then made between three tone sexes: a diatonic, a chromatic and an enharmonic. However, these are not to be equated with our current terms of diatonic , chromatic and enhharmonic . According to legend, the enharmonic sex is an invention of the Olympos .
In the use of the chromatic and enharmonic tones, the two inner tones of the tetrachord were shifted towards the target tone. In the chromatic gender, this shift could be a semitone and in the enharmonic one about a quarter tone . So the Paranete and Trite, respectively Lichanos and Parhypate, could be shifted, while the border tones of the tetrachord (Nete and Hypate, respectively Mese, Paramese and Proslambanomenos) were considered unchangeable.
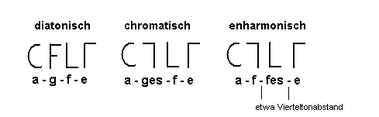
The structure of the chromatic tetrachord is 1½ - ½ - ½, the enharmonic (approx.) 2 - ¼ - ¼. This resulted in 'compressed' tone sequences, also called pyknon (pyknós = compressed).

Example of the tetrachord agfe in the three clay sexes:

Three tone gender example: PNG

We see the tetrachord with the symbols of the instrumental notation . For the diatonic “version” characters from the first row are used, with only the note f being denoted by the character from the second row at the position of the e. This indicates that the semitone above e is meant - i.e. f.
The distinction between chromatic and enharmonic tone gender cannot be made using the notation. In the chromatic gender, the second tone is clearly identified with the sign of the 3rd row at the position of the e (compared to the diatonic gender, the second tone is deepened by a semitone; hence the designation gb instead of f sharp). In the case of the enharmonic sex, the second and third characters are only 'makeshift solutions' so that at least the original tetrachord remains recognizable (see above: structures of the clay sexes). It can be assumed that the choice of making music in the chromatic or enharmonic gender could only be accomplished as a soloist (at least in solo passages).

Regarding the divergence of notation and execution described, one must know that the Greeks understood the shifts within the tetrachord as colors (cf. chroma = "color") that correspond to subjective expressive needs. A distinction was made between the two tone genders, but no further characters were included in the system of symbols in order to allow clear differentiations. In a sense, music-making had a small 'victory' over the systematization that was laid down in writing. At that time, Plato (472–347 BC) still vehemently railed against this individualization of music, quasi a 'softening' of the cosmological order in which he firmly believed.
Furthermore, various music theorists of the time tried to systematize or precisely define the basically irrationally small tone steps in the enharmonic gender. Aristoxenus of Taranto (around 354-300 BC), for example, depicts different interval ratios for these tone steps , known as Diesis . But since the human ear is the 'supreme judge' for him, he declares attempts at finer differentiations below the quarter tone irrelevant . He is concerned with the aurally perceptible clarity of an interval. Aristoxenos polemicized against the thoroughly rationalized recording of music through expressions in numerical proportions, which he, analogously, used technocratic.
This is not surprising: as a pupil of Aristotle , the motto of the ethos was true for him , according to which man is the measure of all things ( Protagoras ). Since the development of the ancient Greek music theory, which has come down to us, falls into this time, the determination of the smallest interval in the enharmonic gender as `` about a quarter tone '' is probably most appropriate.

Keys: octave genres and transposition scales

The octave genres are nothing more than different octave excerpts from the two octaves of the Sýstema Teleion. Due to the different tetrachord structure, the different positions of the semitone steps, scales of different characters result.

The center of the system was the Doric octave genus e'-e. The octave from d'– d was Phrygian, c'– c Lydian, h – H Mixolydian. The names are derived from the ancient tribes of the Dorians , Phrygians and Lydians . The Greek octave genres are not to be confused with the church modes or modes of the Middle Ages - they have nothing more in common than the name.

The octave genres, as excerpts from the entire material scale of the Sýstema Teleion, only played a relative role in this form in the practical music of ancient Greece. The music fragments that have been handed down almost never suggest a consistent application of these scales or cannot be derived from the notation examples.
In the case of theorists and philosophers, however, the Doric, Phrygian, etc. are discussed: Plato and Aristotle discussed them from an ethical point of view. Socrates (in Plato's Politeia in the ideal state), for example, saw specific character traits in the various tone scales or modes and was able to imagine some as a means of education (Doric for the formation of masculinity), while others (e.g. the "soft" Lydian) reject be. These scales can also be found among the old poets.
What the philosophers very likely meant, however, were probably less the regular forms of the octave genres, but rather the use of certain tone formulas, in which hierarchies of certain tones and intervals.
The music theorists Aristoxenos , Ptolemaios as well as the later Aristeides Quintilianus handed down and systematized different numbers of scales which, although basically using the terms Doric, Phrygian, Lydian and Mixolydian, go far beyond these four types. These are the so-called transposition scales (tónoi or trópoi), which had a much clearer reference to musical practice than the octave genres.

The secondary scales of the octave genres, as shown in the illustration below, which are denoted by the addition “hypo-” (= “under”), come from the system of transposition scales. The fact that they are assigned to the octave genres is a late and incorrect representation, which is more due to inferences from the medieval modes of the same name.
The principle of the secondary scales can be imagined as follows: The position of the fifth and fourth, which make up the octave, is reversed: e'-e is Doric; if the upper tetrachord e'-h is shifted an octave lower, the new octave genre is the hypodoric (ae / eh). The hypo scale is thus the closest relative (fifth relationship).

The eight octave genera of the Greeks are:

The eight octave genres of ancient Greek music

Transposition scales

Instead of using rigid scales, the musical practice of ancient Greece knew the insertion of tones that were not related to the ladder and often modulated . In addition, there is the mobility of the internal notes of a tetrachord; only the outer tones were considered to be fixed (see The tone sexes ). Within the central octave, the so-called Harmonia (Néte diezeugménon - Hypáte méson or e'-e), which was considered to be the excellent music-making area, for example: B. one and the same melody with different notation symbols (comparable to our accidentals) can be played.

The actual introduction of the transposition scales (tónoi or trópoi) is more likely to go back to changing to different scale excerpts within a piece of music. The traditional music fragments show modulations. The basic sound system structure of the Sýstema Teleion was regarded as ametábolon, as unchangeable. However, the practice of music provided with the transposition scales an expanded scale theory that made the Teleion system into an emmetábolon, a changeable, modulatable one. So the inclusion of the tetrachord synemmenon is, strictly speaking, already a modulation.

The most important tone level is the Mése (roughly comparable to our dominant ); it represents the center from which the further tones are judged. Kleoneides , adopting the Aristoxenean doctrine, speaks of "simple, double, triple and multiple systems", which means nothing other than the multiple composability of different tone scales. A simple system does not modulate and has a mése that has a whole step above it and is thus diázeuctic. If there are other tones that also reveal the function of a mése, you are dealing with a modulating system that records several tone scales (i.e. transposition scales).
The theorists have given differently large sets of possible transposition scales; Aristoxenos has 15, Aristeides Quintilianus 13.
Ptolemy, on the other hand, started from the octave genera and assumed that these all project into one octave range, i.e. H. let transpose.
According to Ptolemy, the principle of the transposition scales can be represented most easily. He knew seven transposition scales derived from the octave genres: Doric, Phrygian and Lydian each had a sub-fifth scale (Hypo ~). The recess of the Hypomixolydic avoided confusion with the Doric. If you look at Doric as the central scale in the range Néte diezeugménon - Hypáte méson (e'-e) according to the octave genres, the following transposition scales result from transposing the other scales into this range:

Transposition Scales after Ptolemaios Transposition Scales after Ptolemaios.png

The identification of the different transposition scales from original notations is only possible with precise knowledge of the notation conventions . Furthermore, a transposition scale does not in itself have a modal character; it does not correspond to any particular mode per se, as was the case with the medieval tone scales, which borrowed the ancient names. Only the type of combination of notation symbols or how they change can indicate which transposition scale a particular turn of phrase or passage is taken from.
An approximate decision about which tone sex has probably been used is then also permissible here. Modulations can be read at a changing position of the Mése. If, however, within an identified passage in the tetrachord, the tone below the mése takes the position of the parhypáte due to the notation, it can be the diatonic or the chromatic gender. If the parhypáte is replaced instead by a sign for the lichanós and if it is consequently a double tone spacing Mése-Lichanos, then it is the enharmonic gender. However, the predominant assumption in research is that the enharmonic gender was the predominant application.

Somewhat comparable to our major / minor system, the system of transposition scales did not depend on fixed vocal or fundamental tones. These could be adapted to the requirements of the vocal range or the technical possibilities of certain instruments. Thus, e.g. B. Doric not firmly on the root e or Lydian on the root c.
Compared to the late tradition of the Ptolemaois, however, the system of transposition scales, as conveyed by Aristoxenus and Aristeides Quintilianus, probably had a closer relationship to musical practice. It basically also uses the names from the octave genres, but otherwise has no relation to them. Rather, a reference to the development of musical notation becomes clear. Their core symbols for the diatonic tones can be found in the octave f'-f. Characters were added later for tones outside this octave range and for tone steps smaller than a whole tone. Due to the peculiarities of the notation - almost only symbols of the basic sequence - hypolydic can be seen as the central transposition scale. In a modern rendition, Hypolydian would have had a keynote and a Mése d. Doric z. B. would however be displayed with 5 ♭ . According to Aristoxenus and Aristeides, this results in a system that arranges according to semitone steps. Even if new names for transposition scales were added - iastic, aeolian - the relationship between fifths, i.e. H. Pairs with hypo and sometimes also hyper scales ("hyper" = "over") between keys are taken into account.

Ancient music theory tradition

Some of the oldest sources on the tetrachords go back to Greek philosophers and mathematicians. More information can be found in the descriptions of the Greek philosophers and mathematicians. Philolaos - music theory section , Archytas - music section , Aristoxenos - harmonics section , Euclid - music theory section . Ptolemy wrote the three-book harmony , the most important preserved music theory work of late antiquity after Aristoxenus and Euclid. He tried - as probably already Eratosthenes  - a compromise between Aristoxenus and the Pythagoreans , on which Boethius later also orientated himself . Mathematically, he represented the position of Euclid, ideally and terminologically, however, the doctrine of Aristoxenus based on musical perception. In his harmony he handed down many details from older ancient music theorists, such as the tetrachords (tone types) of Archytas, Eratosthenes and Didymos , which would otherwise be lost. A large number of music-theoretical treatises by ancient Greek writers has survived. The oldest documents from the 5th century BC BC contain the equations of the Pythagorean Philolaos about harmony. Plato's contemporary Archytas included proportions with the number 5 and 7 to represent the three tone sexes, thus going beyond the number 3 of the Pythagoreans. The 19th chapter of the problems of Aristotle and the 5th chapter of the 8th book of his republic have musical content . The surviving writings of Aristotle's pupil Aristoxenus on harmony and rhythm are of great importance ; he is the most important ancient music theorist; He took a position opposite to the acoustic thinking of the Pythagoreans and developed a music theory based on auditory perception, which later coined the musical terminology. An important musical script from the Pythagorean school has survived from his younger contemporary, the mathematician Euclid .

The music theorists of the Hellenistic epoch, to which Eratosthenes and Didymos belonged, are a major tradition . Only from late antiquity have other music-theoretical writings survived. Pseudo-Plutarch's interesting work on music comes from the 1st century AD. The writings of the younger Pythagoreans Ptolemaios , Nicomachus and Theon of Smyrna and the Aristoxene Aristeides Quintilianus , Kleoneides = (Pseudo-Euclid) are dated to the 2nd century. , Gaudentios and Bakcheios . The 3rd century includes the Ptolemy commentary by Porphyrios , the scale tables by Alypios and the musical notes of Book 14 by Athenaeus and Chapter 26 by Iamblichus of Chalkis .

The Byzantine era includes the syntagma of Psellos from the 11th century, the harmonics of Bryennios and Ptolemy commentaries by Nikephoros Gregoras and Barlaam of Calabria from the 14th century.

A Latin revision of Greek music theory, especially based on Nicomachus, is the work De institutione musica des Boëthius , which, with the legend of Pythagoras in the smithy, had a significant influence on the music theory of the Middle Ages.

See also

Source collection

  • Egert Pöhlmann (Hrsg.): Monuments of ancient Greek music: collection, transfer and explanation of all fragments and forgeries (= Erlanger contributions to linguistics and art studies 31). Carl, Nuremberg 1970, DNB 720062128 .

literature

Overview representations in manuals

Introductions and general presentations

Investigations on individual topics

  • Helmut Brand: Greek musicians in cult. Dettelbach 2000, ISBN 3-89754-153-X .
  • Katherina Glau: Recitation of Greek choral poetry: the Parodoi from Aeschylus 'Agamemnon and Euripides' Bacchus as a sound sample on CD with text and accompanying booklet. Winter, Heidelberg 1998, ISBN 3-8253-0753-0 .
  • Oliver Busch: Logos Synthesis - The Euclidean Sectio Canonis, Aristoxenos and the role of mathematics in ancient music theory. Berlin 1998, ISBN 3-922378-17-X (also master's thesis)

Web links

Individual evidence

  1. ↑ a b c d Karl Schnürl: 2000 years of European music writings. An introduction to notation studies. Vienna 2000.
  2. ↑ Stefan Hagel: Modulation in ancient Greek music. Frankfurt am Main 2000, p. 11 ff.
  3. ^ Keyword Pyknon in: Willibald Gurlitt , Hans Heinrich Eggebrecht (Ed.): Riemann Musik Lexikon (subject part) . B. Schott's Sons, Mainz 1967, p. 761 .
  4. ↑ Aristoxenos of Taranto: Melik and Rhythmics of Classical Hellenism. Ed. And transl. by Rudolf Westphal. Hildesheim 1965.
  5. ↑ Stefan Hagel: Modulation in ancient Greek music. Frankfurt am Main 2000, p. 27 f.
  6. ↑ Stefan Hagel: Modulation in ancient Greek music. Frankfurt am Main 2000, p. 33 f.
  7. ↑ Stefan Hagel: Modulation in ancient Greek music. Frankfurt am Main 2000, p. 35 f.
  8. ↑ Stefan Hagel: Modulation in ancient Greek music. Frankfurt am Main 2000, p. 166 f.