Claudius Ptolemy

Claudius Ptolemy ( ancient Greek Κλαύδιος Πτολεμαῖος Claudius Ptolemaeus , Latin Claudius Ptolemy ; * 100, possibly in Ptolemais Hermiou , Egypt , † after 160, probably in Alexandria ) was a Greek mathematician , geographer , astronomer , astrologer , music theorist and philosopher . He lived in Alexandria in the Roman province of Egypt . In particular, his three works on astronomy, geography and astrology were considered standard scientific works and important data collections in Europe until the early modern period .
Cassiodorus still had the geographical work in 561/62 , but it was not until the Latin translation of a copy from Constantinople, which was made in Florence from 1397, that the Geographike Hyphegesis was received again.
Ptolemy wrote the Mathematike Syntaxis ("mathematical compilation"), later Megiste Syntaxis ("largest compilation"), today Almagest (derived from the Arabic al-maǧisṭī ) called treatise on mathematics and astronomy in 13 books. This work remained the standard work of astronomy in Europe until the end of the Middle Ages. In addition to a detailed catalog of stars, it contained a detailed elaboration of the geocentric worldview , which was later named after him the Ptolemaic worldview .
In doing so, like most of his contemporaries, he rejected the heliocentric worldview represented by Aristarchus of Samos and Seleukos of Seleukia , which was only to be implemented in Europe 1400 years later by Nicolaus Copernicus , Johannes Kepler and Galileo Galilei .
Life
Little is known about the life of Ptolemy, essentially only what he himself passed down in his works. These are dates from astronomical observations, the oldest from March 26, 127, the youngest from February 2, 141. In a later comment it is stated that he lived under Emperor Hadrian and until the reign of Marcus Aurelius . Only Alexandria is mentioned in his astronomical observations and there is no reason to assume that he ever lived anywhere else. The astronomer Theodoros Meliteniotes wrote around 1360 that he was born in Ptolemais Hermiou, which is otherwise not proven. His name Ptolemy suggests Greek or Hellenized ancestors and his origins in Egypt, the first name Claudius that one of his ancestors under Emperor Claudius or Emperor Nero , the Roman citizenship acquired.
Ptolemy mentions only two contemporaries, a certain Syron, to whom he devoted his astronomical and astrological works, and a certain Theon, who shared observations with him.
He published his works in Greek . The earliest of his main works, the Almagest, was written between 141 - the time of the last observation recorded there - and the inscription by Kanobos , which was set in the tenth year of the reign of Emperor Antoninus Pius (147/148) and which contains partially improved details from the Almagest. Since so little was known about him, he apparently lived a secluded life, but had to come from a wealthy family, which enabled him to occupy himself with mathematics and astronomy. He was also well versed in philosophy, especially Platonic and Aristotelian philosophy , as well as mathematics, but had little interest in biology and medicine. In his time, Alexandria no longer had the same position as a research center as in the Hellenistic period , but was still an important center of astronomical research. The Alexandria Library will have been an important working tool for Ptolemy's work.
astronomy
Ptolemaic worldview
According to Ptolemy, the earth is firmly in the center of the universe, the Centrum Mundi . All other celestial bodies (moon, sun, the five planets known at the time and the starry sky) move in crystalline spheres on circular paths (deferent) around their center, Centrum Deferentis, which are regarded as perfect . The movement on the defender is not uniform. However, there is one more point from which the movement on the deferent appears uniform. This is the Aequantis Center. All three centers lie on one line (line of centers) and are offset from one another by the eccentricity of the planet. In order to bring astronomical observations, in particular the temporary backward movement of the planets, into harmony with this system, it was necessary, however, to let all celestial bodies move further circles (epicycles) around these deferents on their orbits - see epicyclic theory - and in some cases further movements around rotating the primary epicycles, or the line of centers (lunar theory and Mercury theory). By using such orbits (slightly inclined towards each other) Ptolemy was able to bring his model into line with the observations that were still open-eyed at the time .
In the language of today's mathematics, Ptolemy's type of calculation could be described as the empirical forerunner of Fourier analysis , with which the secondary periods of the planetary orbits (including the midpoint equation ) were empirically determined.
The Ptolemaic worldview was superior to the heliocentric worldview of Nicolaus Copernicus (16th century) in the accuracy of its orbit prediction . The Ptolemaic system was replaced around 1600 by the still geocentric tychonic world system (named after Tycho Brahe ). It was only Kepler's discovery that the planets revolve around the sun on ellipses that led to a model of the Copernican worldview that was then sufficiently accurate and generally accepted by astronomers . Ptolemy's calculation methods were extremely precise and correct in their basic idea as a calculation method, but not in their philosophical interpretation that everything revolves around the earth as the center. The breakthrough and success of Kepler's calculations was less due to the fact that the sun and no longer the earth was at the center of the movements, but rather to the fact that Kepler used elliptical orbits instead of circular orbits, which leads to a greater agreement with those of Tycho Brahe and later Galileo Galilei actually conducted measured planetary data.
criticism
In recent times, however, Ptolemy's achievements have been assessed much more critically. Even Tycho Brahe spoke of "fraud" around 1600. In 1817, the French astronomer and mathematician Jean-Baptiste Joseph Delambre accused him of falsified and fabricated observations, preconceived notions, lies and plagiarism. This was repeated in full in 1977 and again in 1985 by the American astronomer Robert Russell Newton . According to Newton, almost all observations allegedly made by Ptolemy himself are fictitious or taken from Hipparchus , whose length information was only added 2 ° 40 ', the value of the accumulated precession (3 ° 40' would have been correct). BL van der Waerden endorsed this damning judgment of Ptolemy in his book The Astronomy of the Greeks , published in 1988 .
On the other hand, as early as 1796, Pierre Simon Laplace presented a simple explanation: The difference of one degree of arc can be explained by an equally large error in the theory of the movement of the sun at that time. Bradley E. Schaefer came to the conclusion in 2002 that Ptolemy (or his assistants) had obtained a considerable number of the observation data mentioned by him. However, if older data fit his model better than his own, he took it over without expressly citing the source. This approach was common at a time when scientific work was not yet subject to today's standards.
Other works
Another astronomical work of Ptolemy are his "planetary hypotheses", in which he used the results of the Almagest to make statements about the dimensions of the universe on a large scale. Based on his model, he estimated the mean distance to the sun as 1,210 (actually: 23,480) and the distance to the fixed star sphere as 20,000 earth radii. It also shows how a clear mechanical model of the cosmos can be built.
Another collection, especially intended for practical purposes, is his "Handy Tables". In the phaseis (rising and falling of the stars with weather signs ) he also put together a star catalog based on the course of the stars over the whole year and expanded that of Hipparchus by about a quarter. He wrote the two writings Analemma and Planisphaerium for the application of mathematics to astronomical questions . Also worth mentioning from an astronomical point of view is the inscription of the canoe on a stele .
Ptolemy assigns dates from the Egyptian calendar to his chronological information relating to astronomical records . In order to avoid ambiguity, he names the beginning and ending ancient Egyptian day for nocturnal events . Due to the precise information, the respective occurrences in the Julian calendar can be precisely dated.
mathematics
The only known independent mathematical work is the treatise on the postulate of parallels , which has only survived in Proklos , in which he wanted to provide a proof for Euclid's axiom of parallels , but which is mathematically incorrect. Other mathematical explanations were incorporated into the above-mentioned primarily application-oriented astronomical writings.
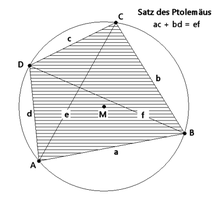
This is how he wrote Ptolemy's theorem . This mathematical theorem applies to chordal quadrilaterals, i.e. quadrilaterals to which a circle can be constructed through all four corners. Ptolemy's theorem says that for a quadrilateral chord, the sum of the product of the opposite side lengths is the product of the two diagonals. Hence ac + bd = ef . Since symmetrical trapezoids also have a circumference, the special case ac + b 2 = e 2 is obtained for the symmetrical legs b = d and the diagonals e = f . The sentence also applies to rectangles that also have a circumference. Here then a = c applies , so that Ptolemy's theorem contains the Pythagorean theorem as a special case: a 2 + b 2 = e 2 . Like the Pythagorean theorem, Ptolemy's theorem is reversible.
In Almagest (I 10) there is following construction of the side lengths of the regular five - or decagon : For given radius (diameter [AB]) of the desired five- or decagon the radius [OB] is halved (center point M) and the circle around M drawn by C. The point of intersection of this circle with the diameter [AB] is point D. Then = OD is the side length of the associated decagon and = CD that of the associated pentagon . In addition, = r = OC is the side length of the associated hexagon. The construction is based on two sets of the elements of Euclid , namely XIII 10 ( ) and XIII 9 ( ) as well as construction II 11 ( continuous division ).
For his astronomical calculations in the Almagest, Ptolemy uses the angle function chord, which is no longer in use today : is the length of the chord to the central angle in the unit circle. This function is tabulated in Chapter I.11 for the range up to with increments . Such tendon tables served the same purposes as sine tables, since:
The information from the Almagest should serve as an example of the accuracy achieved:
In the sixties system, this means
This achieves around 5-digit accuracy, as the comparison shows:
The following applies in the figure:
- and
In the unit circle, the Pythagorean theorem then has the form:
geography
In addition to the comprehensive canon of important cities , Ptolemy wrote the Geographia ( Geographike Hyphegesis , Explicatio geographica , "geographical guide"), in which he recorded the known world and its inhabitants.
As a reference for longitudes (± 180 °), he defined the meridian used until the 19th century by what he called “makaron nesoi” (Latin: “insulae fortunatae” ), today's Canary Islands ( Ferro-Meridian ). His definition of latitude is still valid today (equator 0 °, poles ± 90 °). In addition, he sets out his hypothesis of the unknown southern continent Terra Australis . Ptolemy, like Aristotle earlier, knew that the earth is a sphere; he presented several suitable projections for their representation in one sheet level. He also made various improvements to the earlier work of Marino of Tire . However, he used information from second hand or legends, so that his representations, especially of the peoples treated, are often inaccurate or even misleading. He also dealt with the calculations of the circumference of the earth by Eratosthenes and Poseidonios . In doing so, he took over the wrong results of the latter, which then passed into the generally known literature and, up to Christopher Columbus , led to the conclusion that the earth's circumference of approx. 17,000 nautical miles (30,000 km) was too small .
Ptolemy only handed down written instructions and tables for creating maps, but only drew a few rough sketches himself. Geographies were later written in his name and supplemented by numerous maps over the centuries.
Music theory
Ptolemy also wrote the three-book “ Harmonik ”, the most important surviving music theory work of late antiquity after Aristoxenus and Euclid . He tried - as probably already Eratosthenes - a compromise between Aristoxenus and the Pythagoreans , on which Boethius later also orientated himself . Mathematically, he represented the position of Euclid, ideally and terminologically, however, the doctrine of Aristoxenus based on musical perception. In his harmony he handed down many details from older ancient music theorists, such as the tetrachords (tone types) of Archytas , Eratosthenes and Didymos , which would otherwise be lost.
Optics and Epistemology
His work Optics deals with the properties of light . It deals experimentally and mathematically, among other things, with reflection , refraction and colors. In addition to optical illusions mentioned. In the philosophical treatise peri kriteriou kai hegemonikou (Latin de iudicandi facultate et animi principatu , "Of the power of judgment and the understanding") he represents a mixture of Neoplatonic and Stoic views.
In addition, he also wrote the two-part work Criterion for Epistemology, according to which reason alone is sufficient for the knowledge of truth. He also goes into the thinking of animals and determines the so-called hegemonicon , the functional center of the body, on the one hand for "life" in the heart and on the other hand for making ethical decisions d. H. to the "good life" in the brain.
astrology
In addition, Ptolemy wrote the four-volume astrological basic work Tetrabiblos ("four books"; Greek Ἀποτελεσματικά Apotelesmatika was perhaps the title of the work given by Ptolemy himself), which is based on his astronomical writings and the fundamentals of astrology and the effects of the heavenly bodies on the earthly sphere and matter as well as man.
Namesake
The lunar crater Ptolemy was named after him in 1935, Mount Ptolemy in Antarctica in 1962 , as was Lake Ptolemy in Nubia.
Text output
- Johan Ludvig Heiberg (Ed.): Claudii Ptolemaei opera quae exstant omnia . Teubner, Leipzig, Volume I (Syntaxis, also Almagest) in two volumes 1898, 1903, Volume II (Opera astronomica minora), 1907. Part III, 1 (Tetrabiblos) was edited by Franz Boll, Emilie Boer and appeared in 1954 (and 1998 edited by Wolfgang Huebner ), Part III, 2 (fragments, dubious works) was published in 1952, 1961 by Friedrich Lammert .
- Claudius Ptolemy: Tetrabiblos. Based on the rare edition from 1553 obtained by Philipp Melanchthon . 2nd Edition. Chiron, Tübingen 2000, ISBN 3-925100-17-2 . ; 3rd edition ibid 2012.
- Frank E. Robbins (Ed.): Ptolemy Tetrabiblos , Loeb Classical Library, Harvard University Press 1940.
- Ingemar Düring: The harmony theory of Klaudios Ptolemaios . Elander, Gothenburg, 1930; Reprinted by Olms, Hildesheim 1982.
- Jon Solomon (Ed.): Ptolemy. Harmonics , Mnemosyne, Bibliotheca Classica Batava, Supplementum, Leiden: Brill 2000 (English translation)
- AM Smith (Ed.): Ptolemy's theory of visual perception: An English translation of the Optics with introduction and commentary , Transactions of the American Philosophical Society, Volume 86, Part 2, Philadelphia 1996.
- A. Lejeune (Ed.): L'optique de Claude Ptolémée , Löwen 1956 and Leiden: Brill 1989 (Latin / French)
For the editions of the Almagest and Geographike Hyphegesis and related literature, see there.
literature
Overview representations in manuals
- Jacqueline Feke, George Saliba: Ptolémée d'Alexandrie (Claude) . In: Richard Goulet (ed.): Dictionnaire des philosophes antiques , Volume 5, Part 2 (= V b), CNRS Éditions, Paris 2012, ISBN 978-2-271-07399-0 , pp. 1718-1735.
- Wolfgang Huebner : Klaudios Ptolemaios. In: Christoph Riedweg u. a. (Ed.): Philosophy of the Imperial Era and Late Antiquity (= outline of the history of philosophy . The philosophy of antiquity. Volume 5/1). Schwabe, Basel 2018, ISBN 978-3-7965-3698-4 , pp. 493-512, 528-536
- Erich Polaschek: Klaudios Ptolemaios as a geographer. In: Paulys Realencyclopadie der classischen Antiquity Science (RE). Supplementary volume X, Stuttgart 1965, Col. 680-833.
- Gerald J. Toomer : Ptolemy (or Claudius Ptolemeus) . In: Charles Coulston Gillispie (Ed.): Dictionary of Scientific Biography . tape 11 : A. Pitcairn - B. Rush . Charles Scribner's Sons, New York 1975, p. 186-206 .
- Konrat Ziegler u. a .: Klaudios Ptolemaios. In: Paulys Realencyclopadie der classischen Antiquity Science (RE). Volume XXIII, 2, Stuttgart 1959, Sp. 1788-1859.
Investigations
- Franz Boll : Studies on Claudius Ptolemaeus. A contribution to the history of Greek philosophy and astrology . In: New Yearbooks for Philology and Education. Supplementary volume 21.2. Teubner, Leipzig 1894, pp. 49–244.
- Alexander Jones (Ed.): Ptolemy in perspective: use and criticism of his work from antiquity to the nineteenth century. Springer, Dordrecht a. a. 2010.
- Klaus Geus : Ptolemy - reactionary, theorist, plagiarist? In: Thomas Beck u. a. (Ed.): Barriers and accesses. The history of European expansion. Festschrift for Eberhard Schmitt on his 65th birthday. Harrassowitz, Wiesbaden 2004, ISBN 3-447-04848-4 , pp. 36-50
- Gerd Graßhoff: The history of Ptolemy's star catalog . Springer, New York a. a. 1990, ISBN 0-387-97181-5 .
- Wilfried Neumaier: What is a sound system? A historical-systematic theory of the occidental sound systems, based on the ancient theorists, Aristoxenus, Eucleides and Ptolemaios, represented by means of modern algebra . Lang, Frankfurt am Main a. a. 1986, ISBN 3-8204-9492-8 .
- Ingemar Düring : Ptolemaios and Porphyrios on music . Göteborg 1934, reprint Olms, Hildesheim 1987, ISBN 3-487-07932-1 .
Web links
- Literature by and about Claudius Ptolemy in the catalog of the German National Library
- Works by and about Claudius Ptolemy in the German Digital Library
- John J. O'Connor, Edmund F. Robertson : Claudius Ptolemy. In: MacTutor History of Mathematics archive .
- On the sentence of Ptolemy, State Education Server Baden-Württemberg
- Klaudios Ptolemaios as a geographer ( Memento from December 23, 2005 in the Internet Archive )
- Literature on geography (Geographike Hyphegesis) by Claudius Ptolemaeus ( Memento from June 5, 2008 in the Internet Archive )
- Biography de Ptolémée (French)
- Works by Claudius Ptolemy in the complete catalog of incandescent prints
Texts Almagest
- Almagest Books 1-6 - Greek text with Latin introduction in the Internet Archive
- Almagest books 1-13 - Greek text (edition by Heiberg, PDF)
- Almagest - digitized version of an edition from 1515 (University of Vienna, Latin translation, several resolutions, PDF)
Geography
- Claudii Ptolemaei Geographia, ed. 1843, tom. I (Books 1-4); 1845, tom. II (Books 5-8); 1845, tom. III (Register) - Greek text from the Tauchnitz edition (Google Books)
- Geographike - analytical extract from several chapters of books 2–5 on the website LacusCurtius by William P. Thayer (University of Chicago), Germania Magna and others in Greek / Latin / English, others only in English (translation by Edward Luther Stevenson (New York, 1932) - discrepancy between antique and Stevenson's chapter numbering)
- Claudii Ptholemaei Alexandrini liber geographiae cum tabulis et universali figura et cum additione locorum quae a recentioribus reperta sunt diligenti cura emendatus et impressus - Latin translation (Venice 1511, digital copy of the University of Alabama)
- Geographics Book 8 - Greek Text by Aubrey Diller (PDF)
Tetrabiblos
- Tetrabiblos on LacusCurtius (English translation by Frank Egleston Robbins, Loeb Classical Library)
- Tetrabiblo's full English translation by JM Ashmand (1822)
- Claudius Ptolemaeus: Ptolemaei libri IV mathematicae translatione Wintomiensis Ebdelmessiae - Mscr.Dresd.Db.87 . [Sl] 1450, digitized version of the Saxon State Library
Digital copies
- Johannes Regiomontanus, Georg von Peuerbach, Claudius Ptolemaeus: Ioannis De Monte Regio Et Georgii Purbachii Epitome, In Cl. Ptolemaei Magnam compositionem . Basileae 1543, digitized version of the Saxon State Library
Footnotes
- ↑ Gerald J. Toomer: Ptolemy. In: Dictionary of Scientific Biography. Volume 11, New York 1976, pp. 186-206.
- ^ Thomas Szabó: Florence and the measurement of Europe . In: Marina Montesano: “Come l'orco della fiaba”. Studi per Franco Cardini . SISMEL. Edizioni del Galluzzo, Florenz 2010, pp. 595–626, here: p. 595.
- ↑ Gerald J. Toomer, Ptolemy (or Claudius Ptolemaeus). In: Dictionary of Scientific Biography. Volume 11. Charles Scribner's Sons, New York 1975, p. 186
- ↑ Gerald J. Toomer, Ptolemy (or Claudius Ptolemaeus). In: Dictionary of Scientific Biography. Volume 11. Charles Scribner's Sons, New York 1975, p. 187
- ↑ Alexander Jones : Claudius Ptolemy - influential astronomer and astrologer from Alexandria. In: Akademie Aktuell. Bavarian Academy of Sciences. Issue 3, 2013, pp. 14–17, here p. 14 ( online ).
- ↑ Gerald J. Toomer, Ptolemy (or Claudius Ptolemaeus). In: Dictionary of Scientific Biography. Volume 11. Charles Scribner's Sons, New York 1975, p. 187
- ↑ Paul Kunitzsch : Ptolemy and astronomy: The Almagest. In: Akademie Aktuell. Bavarian Academy of Sciences. Issue 3, 2013, pp. 18–23, here p. 19 ( online ).
- ^ Christian HF Peters , Edward Ball Knobel: Ptolemy's Catalog of Stars. A Revision of the Almagest. Washington 1915 (= Carnegie Institution of Washington. Publication No. 86).
- ↑ Tristan Thielmann: Source Code of Orientation. A design by Leon Battista Alberti. In: Sabiene Autsch, Sara Hornäk (Ed.): Spaces in Art. Artistic, art and media studies designs. transcript Verlag, Bielefeld 2010, ISBN 978-3-8376-1595-1 , pp. 231–250, here: p. 235.
- ^ SNAC - Stevenson, Edward Luther, 1858-1944
| personal data | |
|---|---|
| SURNAME | Ptolemy, Claudius |
| ALTERNATIVE NAMES | Πτολεμαῖος, Κλαύδιος (Greek); Ptolemaíos, Klaúdios; Ptolomaeus, Claudius (Latin) |
| BRIEF DESCRIPTION | Greek mathematician, geographer and astronomer |
| DATE OF BIRTH | at 100 |
| PLACE OF BIRTH | Ptolemais Hermeiou , Egypt |
| DATE OF DEATH | before 180 |
| Place of death | Alexandria , Egypt |