Reflection (physics)

In physics, reflection ( Latin reflexio , backward bend , from the verb reflectere , backward bend , backward ) describes the throwing back of waves at an interface at which the wave resistance or the refractive index of the propagation medium changes.
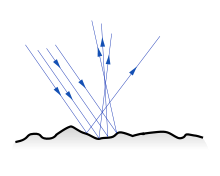
The law of reflection applies to smooth surfaces ( i.e. small roughness structures compared to the wavelength ) ; the case of directional reflection applies . Waves or (depending on the perspective) radiation are diffusely scattered on rough surfaces and in this case Lambert's law of radiation applies approximately .
As a rule, only part of the energy of the incident wave is reflected in the reflection; one speaks in this context of partial reflection (partial reflection). The remaining part of the wave propagates further in the second medium (= transmission ); the wave resistance changes due to the change in direction (cf. refraction ) and speed. The angle of refraction can be calculated with the Snellian law of refraction and the amplitudes of the reflection and transmission with the Fresnel formulas - depending on the wave resistance and polarization .
A special case of reflection is total reflection , in which the wave is completely reflected at the interface when it hits a medium with a lower wave resistance. On closer inspection, this only occurs with ideally transparent media. If, for example, the second medium is absorbent in a certain frequency range, so-called weakened total reflection occurs , in which the reflection behavior changes in this range. Total reflection is used, for example, for retroreflection (reflection of a wave in the direction of the source).
One-dimensional special case
If the wave carrier only allows the wave to propagate in one spatial direction, it is called a one-dimensional wave. Examples would be rope waves, sound waves in narrow tubes (see Kundt's tube ), electromagnetic waves in waveguides , etc. Reflection occurs at the end of such a wave carrier. The incoming wave and the opposite reflected wave overlap. If one ideally assumes that there is no loss of energy (no attenuation, complete reflection), the amplitudes of the incoming and outgoing waves are the same. It formed standing waves from. A distinction is made between the reflection "at the fixed end" and "at the loose end":
- At the fixed end , the deflection of the shaft is zero at all times. The incoming and the reflected waves have a phase difference of π here , i. that is, they are out of phase and interfere destructively. This creates a knot at the fixed end. Further oscillation nodes are each half wavelength apart. The antinodes are in between.
- The deflection of the shaft is maximum at the loose end . There is no phase difference between the incoming and reflected waves; i.e., they are in phase and constructively interfere. This creates a belly at the loose end. Further antinodes are located at a distance of half the wavelength. The nodes of oscillation are in between.
Whether one end is fixed or loose depends on which amplitude size is used to describe the wave. So z. B. an open pipe end for a sound wave is a fixed end when talking about the sound pressure, while it is a loose end for the speed of sound. Sound velocity and sound pressure are phase shifted by π / 2. If reflection takes place at both ends of the wave carrier, standing waves that cannot change over time can only occur if a resonance condition is met:
- If the shaft carrier has two fixed ends or two loose ends, resonance occurs when the length of the shaft carrier is an integral multiple of half the wavelength:
- If one end of the shaft carrier is firm and the other is loose, the resonance condition is:
The standing waves generated in this way are used in many musical instruments . For example, a guitar string is a one-dimensional wave carrier with two fixed ends. If you pluck it, the string vibrates at the frequencies that meet the resonance condition. For we get the frequency of the fundamental. All other frequencies result in the overtone spectrum .
Reflection of individual impulses

A pulse of any curve shape is a wave packet which, according to the rules of Fourier analysis , can be broken down into a sum of sinusoidal oscillations of different wavelengths λ. Only those are allowed between two reflectors at distance A for which the following applies:
where n is a natural number. Under certain conditions, the shape of the curve of the impulse composed of it remains the same and this soliton can oscillate undamped between the two reflectors, as can be seen in the picture. By comparing this pendulum duration with the exact time marks of an atomic clock , one can determine extremely high frequencies ( frequency comb ).
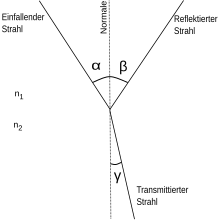
Law of reflection
The law of reflection says that the angle of reflection (also the angle of reflection) is exactly as large as the angle of incidence , and both lie in one plane with the perpendicular, the plane of incidence . In the case of waves, the wavelength must be considerably greater than the distances between the scattering centers (for example atoms). Otherwise, several “reflection rays” can form, for example with X-rays that are reflected off a crystal (see X-ray diffraction ).
The law of reflection can be derived using Huygens' principle (see adjacent figure): In the first and second images you can see how a wave front hits a reflective surface at an angle and generates circular elementary waves around the respective points of impact. The radii of these waves increase with the phase velocity of the wave in the relevant medium. The following pictures show how the resulting elementary waves are superimposed to form a new wave front that runs to the top right. The angles between the incoming and outgoing wave fronts and plane are (mirror-inverted) the same. This is what the law of reflection says.
Another derivation makes use of the Fermat principle : The light path from point A to point B is extremal (more precisely: minimal) if the reflection occurs precisely in such a way that the angles of incidence and reflection are equal.
Directed reflection
The wave field on a directionally reflecting surface can be described by “mirror sources”. For each original source, a mirror source is "attached" behind the reflective surface, at the same distance from the reflective surface as the original source. The wave field results from the superposition of the wave fields from original and mirror sources.
The directional reflection is used in flat and non-flat mirrors , for example concave curved concave mirrors as shaving mirrors or in mirror telescopes . Convex curved mirrors are used as exterior mirrors on motor vehicles.
Diffuse reflection
Boundaries with a large roughness relative to the wavelength reflect diffusely. If the material contains many scattering centers, the reflection follows Lambert's law . The main backscattering then occurs perpendicular to the material, regardless of the direction of irradiation. Examples are milk, wall paint or paper. With milk, the fat droplets in water have the order of magnitude of the wavelength of visible light and form the scattering centers for light waves, the same applies to the air inclusions between the fibers in paper.
Applications of diffuse reflection, i.e. the even distribution of light, are
- Integrating sphere ,
- Projection screen,
- Avoidance of reflective reflections on screens and photographic prints.
The sum of specular and diffuse reflection is also referred to as remission , based on the amount of light emitted by the reflectance . There are different definition options for surfaces that are not perfectly diffuse, curved and possibly color-cast. In meteorology , the albedo indicates the proportion of sunlight that is diffusely reflected from the earth's surface or from clouds. In astronomy , the albedo of other celestial bodies that do not shine by themselves is included in the brightness with which this celestial body can be seen from earth.
Various definitions of whiteness are common in the industry. Some definitions take into account, among other things, that the human eye is more sensitive to some wavelengths than to others.
Reflection of electromagnetic waves in optics

In the following, the reflection will be explained using electromagnetic waves as an example. The ray model of geometric optics is used for easier understanding .
In the schematic drawing (see law of reflection), a ray hits the surface of a medium with different radiation propagation properties from the top left. Part of the radiation is refracted towards the perpendicular (transmitted part), while another is reflected. The law of reflection applies: The angle of incidence is equal to the angle of reflection. However, under suitable conditions, the incident radiation can be completely reflected, as in the case of total reflection.
Electromagnetic radiation is usually only partially reflected at an interface, the other part is transmitted . The reflectance is defined as the ratio of the reflected to the incident light intensity
The degree of reflection can be calculated from the Fresnel formulas using the reflection factor. It depends on the angle of incidence and polarization of the light as well as the properties of the materials involved. In the case of circularly polarized waves, the helicity changes with each reflection .
The refractive index is generally dependent on the wavelength. This means that waves of different wavelengths can be reflected to different degrees. For example, due to the absorption by the electron gas , metals have a high extinction coefficient for electromagnetic radiation in the infrared range; they are therefore opaque and have a very high degree of reflection of generally more than 90 percent. In contrast, the degree of reflection of metals in the visible or ultraviolet range sometimes drops very quickly within a small frequency range (see picture with the example of silver). In reflection spectroscopy one inferences from the measured reflection spectrum about mechanisms effective in the material and their parameters such as the density of electrons in the conduction band or polarizabilities .
Due to the different degree of reflection depending on the angle of incidence and the polarization of the light, this changes with every oblique reflection. That is, if unpolarized light falls on an inclined boundary surface, the reflected and refracted light (at and ) are partially polarized. In the special case , the light component polarized parallel to the plane of incidence is not reflected at all, but is completely refracted ( Brewster's angle ). The reflected part is then polarized completely perpendicularly and the transmitted part contains both polarization directions. This effect makes it possible, for example, to let laser radiation exit the cavity through a Brewster window without loss of reflection .
The index ellipsoid of birefringent materials, which depends on the crystal orientation, has a further influence on the reflection . Here the degree of reflection also differs depending on the crystal orientation of the crystal surface. A magnetic field can also influence the reflection, which is technically used in magneto-optical storage media .
The reflection can be reduced or increased by interference at one or more dielectric layers and is used for anti-reflective coating or for the production of dichroic mirrors .
application
An essential area of application for the reflection of electromagnetic waves or rays is their targeted guidance. The u. a. in the case of the mirror , which for example reflects the light scattered by a person in a directed way so that the person can see himself. Technically, reflection on flat mirrors or prisms is used to deflect beams, for example in periscopes or in the deflecting prism or the folding mirror of reflex cameras .
Reflection can also be used for non-contact detection or measurement of reflective surfaces ( deflectometry ) or for measuring the distance between a radiation source and a reflecting surface (transit time measurement or interferometry). Examples are laser rangefinders , reflex light barriers or time domain reflectometry
Furthermore, the reflection on concave mirrors is used to bundle electromagnetic rays. A directional effect is achieved with parabolic antennas . Examples of optical wavelengths are headlights or reflector telescopes .
The way in which a body reflects light due to its material, shape and surface texture is also used in many creative areas such as product design or architecture . For example, surfaces are polished to create a shiny, reflective impression, or roughened / sanded to give a diffuse reflection. A similar effect can also be achieved with the use of different lacquers (e.g. glossy, semi-gloss, matt).
The type of reflection can have an influence on technical parameters, for example, with matt screens, the disruptive influence of scattered light reflections is reduced with the help of diffuse reflection on a rough surface. Compared to reflective displays, the rough surface also reduces the black impression and the color brilliance of the light transmitted through the protective pane.
Since an intensity component that is characteristic of a material is reflected in the reflection, properties of materials such as refractive index, thickness, impurities, etc. can also be determined in this way. Measurements at a single wavelength as well as spectral distributions are used here ( reflectometric thin-film measurement , ellipsometry ). The latter form the basis for spectroscopy , in which, in addition to transmission, the reflection of polarized and unpolarized electromagnetic waves is a frequently used examination technique, see reflection spectroscopy .
Reflection on electrical lines
If an electric wave with the amplitude A 0 is guided through a line that is closed with its characteristic impedance , it is completely absorbed there, without reflection and regardless of its frequency. The termination can be a load resistor , an antenna, the input resistance of an analog or digital circuit or one or more other lines. If there is a mismatch - assuming linearity - a reflected wave of the same frequency and (mostly) changed amplitude A R occurs . The ratio A R / A 0 is called the reflection factor :
This includes the impedance of the termination and the characteristic impedance of the line.
Generally is frequency dependent and complex , typically with magnitude less than 1; its argument means a phase change. In practice, a real value is always sought.
Special cases:
- means that the wave is not reflected, so there is no echo. (Case: adapted line ).
- means that the wave is completely reflected (open end = voltage doubling by superimposing the leading and reflected waves).
- means that the wave is fully reflected, but inverted (short-circuited end; voltage = 0 due to superimposition of the leading and reflected waves).
One application is described in the article Time Domain Reflectometry . The leading and reflected waves running on the line can overlap and lead to a location-dependent distribution of current and voltage (standing waves).
Reflection of voltage jumps
If lightning strikes a high-voltage line, a high-voltage pulse runs to the end of the line and can cause destruction there. Something similar can be observed in cables and lines ( ribbon cable , coaxial cable with line impedance Z ) when a voltage jump is fed in - for example by switching the beginning of the cable to a DC voltage. The DC voltage is supplied by a power supply with an internal resistance of R = Z , so that the voltage jump enters the cable without reflections.
Infinitely long cable
If the DC voltage U is applied to an infinitely long lossless cable at the time zero, a constant current I would flow forever :
A constant voltage U / 2 occurs at the feed point regardless of whether and how the cable end is wired . At the feed point you cannot distinguish what is at the end of the cable. The cable stores the electrical energy and after an infinitely long time the cable is “charged” (magnetic field, electrical field).
One can predict the time of the arrival of the voltage jump at a distant measuring point, because the propagation speed of the jump is c medium . The insulation material with the relative permittivity between the conductors of the cable determines the pulse speed in the cable
Finite cable length
If the cable has the finite length L in the above thought experiment , the voltage jump comes after time
at the end of the cable. The conclusion there decides how to proceed:
Reflection-free conclusion
If the inner and outer conductors of the coaxial cable are connected via a resistor R = Z , the electrical energy flows without reflections into this terminating resistor, which heats up accordingly. At the feed point (beginning of the cable) one cannot distinguish this case from an infinitely long cable.
Open end
If the inner and outer conductors are not connected, the voltage jump is reflected in phase. This leads to a doubling of the voltage and the superimposed voltage jump runs with c medium back to the beginning of the cable (see picture above right). Back at the feed point, it is not reflected there because the internal resistance of the power supply corresponds to the line impedance (reflection-free termination). As soon as the voltage jump occurs at the feed point, equilibrium is reached, no further current flows and the voltage U is measured between the conductors at each point on the cable . With a storage oscilloscope , this "tension staircase" can at first U / 2, and then - from the time 2 T to - U record.
Shorted end
If the conductors are short-circuited at the end, the voltage jump is reflected out of phase. The forward and backward waves are superimposed to zero. This is only measured at the beginning of the cable when the reflected voltage jump arrives there after the time 2 · T. This square pulse (zero to U / 2 when switched on and after the time 2 T to zero) can be recorded with an oscilloscope . A cable that is short-circuited at the end acts like a "delayed short circuit".
application
Cables with a defined length that are short-circuited, adjusted or open at the end are used as a timing element (transit time), for pulse delay or storage, as a line circuit ( resonant circuit , trap circuit , filter, impedance transformation, phase rotation) or with a variable length for measuring the wavelength or Frequency used.
See also Lecher line .
Reflection in acoustics
Types of reflections
In acoustics , we mean sound reflection , i.e. the reflection of sound . Flat, reverberant, non-absorbing surfaces reflect the sound waves well. The echo perception threshold plays an important role in recognizing these sound reflections . Depending on the arrangement and number of reflective surfaces and the type of sound reinforcement , the hearing impression varies :
- Echoes (rock face at a greater distance)
- Flutter echo (two parallel reflecting walls)
- Reverberation (large rooms with hard walls, like in churches)
- high spatiality (acoustic sense of space in concert halls)
- dry sound (in rooms with little reflective surfaces)
The following are important for the acoustic impression:
- Share of direct sound in the total sound level
- Time delay and direction of early reflections , as well as their contribution to the total sound level
- Deployment delay and spatial distribution of the reverberation, as well as its share in the total sound level and its temporal course ( reverberation time )
Room acoustic design
In the case of rooms, different room acoustic properties and thus a different reflection behavior of the walls make sense depending on the use :
- Up to a certain limit, anechoic rooms in recording studios (i.e. no anechoic rooms) so that the acoustic character of the recording room has as little influence as possible on the recording.
- Rooms with moderately reflective walls for classrooms. On the one hand, the teacher's voice should be supported by early reflections of up to 15 ms; on the other hand, speech intelligibility should not be reduced by too strong late reflections and too long reverberation times. The favorable reverberation time for normal hearing people according to DIN 18041 "Audibility in small to medium-sized rooms" is between 0.3 and 0.8 seconds, depending on the volume of the room. In classrooms with a volume of 125 to 250 m³, a reverberation time of 0.4 to 0.6 seconds is optimal. For the hearing impaired , reverberation times of around 0.3 seconds should be aimed for.
- Rooms with highly reflective walls and a balance between direct sound, early reflections and reverberation for concert halls. The aim here is to achieve the most "spatial" musical experience possible through early wall reflections that fall sideways onto the ears. A high degree of diffusion , i.e. the scattering of the sound, is also important. A favorable reverberation time is 1.5 to 2 seconds.
A very special significance in the spatial space detection has the initial time gap ( ITDG ).
Relationship between reflection, absorption, transmission
The following variables play a role in sound reflections:
- The degree of sound reflection or is a measure of the reflected sound intensity .
- The sound absorption coefficient or is a measure of the absorbed sound intensity.
- The sound transmittance or is a measure of the sound intensity that is let through.
- The degree of sound dissipation or is a measure of the "lost" sound intensity.
When it hits the boundary surfaces, the incoming sound intensity is either reflected on the boundary surface or absorbed by the boundary surface. It is therefore true
The absorbed portion of the sound intensity is either let through (transmitted) by the boundary surface or converted into heat (dissipated) in the materials of the boundary surface. It is therefore true
Thus applies overall
In acoustics , the following words belong to disturbed sound propagation
Reflection of water waves
At progressive water waves wave reflecting means throwing back a portion of its energy on a structure ( breakwater , embankment ) or in places where the configuration of the natural seabed changes (strong). At the same time, another part of the wave energy is passed on and the remaining part is dissipated and absorbed by the processes of wave breaking , fluid and ground friction, compare wave transformation , wave absorption .
Accordingly, the law of conservation of energy reads:
In it mean
- = Energy of the approaching waves
- = Energy of the waves transmitted (through the structure)
- = Energy of the waves reflected on the structure
- = Energy loss due to wave absorption.
If the energy components mentioned , , each in the relationship with the energy of the incoming waves set such values as can transmission coefficient , reflection coefficient and absorption coefficient are given. Generally the reflection coefficient . Only in the theoretical case of perfect reflection (when there is a perfect clapotis ) is . Only here is the statement that a phase jump does not occur in the reflection on an ideally smooth vertical wall . In particular with partial reflection on steep, level bank embankments, the phase jump can amount to about 180 °, see the adjacent picture.
Since the wave energy to the square wave height is proportional to the reflection coefficient may also be easier as the quotient of the height of the reflected wave and the height of the oncoming wave are written .
Reflection through an attractive potential
In classical mechanics, a reflection can only take place in one dimension at a repulsive potential . In the context of quantum mechanics , however, reflection at an attractive potential is also possible. This contradicting view is called quantum reflection .
Web links
optics
- Radiation optics and reflection Explanation of the reflection of light rays on flat mirrors, concave mirrors and curved mirrors. Patrick Wagner, accessed October 14, 2007 .
- Animation of scattering - reflection on surfaces. Dieter Welz, accessed on October 14, 2007 .
- Reflection and refraction of light - animations. Michael Komma, accessed October 14, 2007 .
Acoustics
- Early reflections of less than 15 ms are undesirable for stereo recordings (PDF file; 36 kB)
- H. Redlich and M. Fouqé: About spatial information in stereophony - application example for reflections (PDF file; 384 kB)
- Importance of reflection in room acoustics
- Importance of diffuse reflection (scattering) in room acoustics
Individual evidence
- ↑ Eugene Hecht: Optics . Oldenbourg Wissenschaftsverlag, 2005, ISBN 3-486-27359-0 , p. 168 ff .
- ^ Dieter Suter: Electronics. (PDF; 3.8 MB) (No longer available online.) Archived from the original on July 4, 2017 ; accessed on May 1, 2017 .