Complex AC bill

The complex alternating current calculation is a method of electrical engineering to describe and calculate the behavior of linear time-invariant systems with sinusoidal alternating voltage and sinusoidal alternating current . These are i. A. described by differential equations, the classic solution methods of which are relatively difficult and unfavorable for "engineering practice". The complex alternating current calculation allows, with certain restrictions, as a symbolic method, the transformation of the differential equations into algebraic equations , the solution of which is much simpler and at the same time easier to interpret. This reduces the calculation of AC networks to the calculation methods of DC networks.

The complex alternating current bill was created at the end of the 19th century to solve the problems of alternating current technology that were then pending. It goes back to the work of Charles P. Steinmetz , who founded the symbolic method of alternating current technology in his dissertation in 1889, and to the dissemination of this theory after 1893 through many works by Arthur Edwin Kennelly . A mathematically exact representation of the applied solution methods with complex voltages and currents was given in 1937 by Wilhelm Quade . In its historical classification complex alternating current calculation is itself a first operational calculus of systems theory and on the other hand by their success the impetus for the development of further Operators bills (eg. B. operational calculus , Laplace transform given). If the requirements are met, this symbolic method can also be used for other (non-electrical) systems.

Spellings, conditions and restrictions

Understanding the complex AC bill requires knowledge of complex numbers and the calculation of electrical networks . It deals with voltages and currents that change over time and that follow a sinusoidal curve. In order to express this variability in relation to the temporally fixed quantities, instantaneous values ​​that change over time are designated with lower case letters, voltages as small  and current intensities as small  . To expressly identify the time dependency, the letter in round brackets can be added to the symbol , e.g. B. . Formula symbols of complex sizes are indicated by an underscore. The letter (with ) is used for the imaginary unit in electrical engineering in order to avoid confusion with the letter used for the (time-dependent) current. ${\displaystyle u}$ ${\displaystyle i}$ ${\displaystyle t}$ ${\displaystyle u(t)}$ ${\displaystyle \mathrm {j} }$ ${\displaystyle \mathrm {j} ^{2}=-1}$ ${\displaystyle i}$

The complex alternating current calculation is only applicable for linear time-invariant systems because it assumes the validity of the superposition theorem. Therefore, all components, such as resistors, capacitors and coils, have to show linear properties in the frequency range under consideration. This does not apply, for example, to coils with magnetic saturation or capacitors whose dielectric constant depends on the electrical field strength . The complex AC calculation is expressly not applicable to assemblies whose main function is based on strong non-linearities (e.g. modulators and rectifiers ), because the non-linearities result in non-sinusoidal signals and thus "new" frequencies. As a rule, the characteristics of semiconductor components are also non-linear. However, if these are operated with small sinusoidal signals in the constant range of characteristics , this characteristic can be linearized and the complex alternating current calculation can be used. In this way, for example, the two-port theory for transistor circuits can only be used.

The complex alternating current calculation is based on sinusoidal electrical or physical quantities in which the transient process that occurred when switching on is so long ago that it no longer has any influence on the behavior of the system. In this steady state, only sinusoidal quantities with the same angular frequency occur within the system . For this reason, only this steady state can be calculated with the complex AC calculation, but not the volatile switch-on process. This is also the reason why switching processes, such as switching direct and alternating voltages on and off, as well as the system behavior in the case of individual pulses or pulse sequences , cannot be analyzed with the complex alternating current calculation alone. However, there are generalized methods based on the complex AC calculation, e.g. B. Fourier series and the Laplace transform , which make these calculations possible. ${\displaystyle \omega =2\pi f}$

In the following, only voltage and current strength are considered as examples, although all statements also apply to other physical quantities.

General Introduction

The determination of the ratio of current to voltage in an electrical circuit is one of the basic tasks of electrical engineering.

If a voltage that is constant over time is specified and the current intensity is determined, or if the current intensity is specified and the voltage is determined, the ratio is called electrical resistance or the ratio is called electrical conductance . ${\displaystyle U}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle U}$ ${\displaystyle {\tfrac {U}{I}}}$ ${\displaystyle R}$ ${\displaystyle {\tfrac {I}{U}}}$ ${\displaystyle G}$

Ohmic resistances, inductances or capacitances occur as passive linear elements of the alternating current circuit . The following applies to these elements:

• Ohmic resistance : the current strength is proportional to the voltage: ${\displaystyle R}$

  ${\displaystyle i={\frac {u}{R}}}$

• Inductance : the change in current intensity is proportional to the voltage: ${\displaystyle L}$

  ${\displaystyle {\frac {\mathrm {d} i}{\mathrm {d} t}}={\frac {u}{L}}}$   or equivalent   ${\displaystyle i\cdot L=\int u\cdot \mathrm {d} t}$

• Capacity : the change in voltage is proportional to the current strength: ${\displaystyle C}$

  ${\displaystyle {\frac {\mathrm {d} u}{\mathrm {d} t}}={\frac {i}{C}}}$   or equivalent   ${\displaystyle u\cdot C=\int i\cdot \mathrm {d} t}$

If one of the specified values ​​- voltage or current intensity (simply current) - is constant, the resulting value is only constant for purely ohmic circuits. The methods of calculation used are then, and only then, those of direct current calculation. An ideal inductance would represent a short circuit, an ideal capacitance an interruption of the current branch. When switching on or off, there is temporarily no periodic process, because the transition is subject to a transient process .

If the specified size is not constant or if the circuit is not purely ohmic, the current / voltage relationship is more complicated. Capacities and inductances must then be included in the calculation via differential equations . However, the calculation can be easier in special cases.

Such a special case exists when the specified variable has a sinusoidal periodic course, e.g. B. a sinusoidal current (see alternating current )

${\displaystyle i={\hat {\imath }}\cdot \sin(\omega t+\varphi _{i})}$

or a sinusoidal voltage

${\displaystyle u={\hat {u}}\cdot \sin(\omega t+\varphi _{u})}$

It is and also the maximum value, and amplitude called, is the angular frequency , and also is the zero phase angle of the alternating size. The difference is called the phase shift angle . ${\displaystyle {\hat {u}}}$ ${\displaystyle {\hat {\imath }}}$ ${\displaystyle \omega =2\pi f}$ ${\displaystyle \varphi _{u}}$ ${\displaystyle \varphi _{i}}$ ${\displaystyle \varphi _{u}-\varphi _{i}}$

The resulting variable then has a likewise sinusoidal periodic course of the same frequency , which, however, can change in the phase shift and the amplitude ratio with the frequency (alternatively the period duration ).

The mathematical treatment of calculations in this regard is advantageously carried out using complex quantities , since these make the solution of trigonometric tasks much easier.

Complex voltage and complex current

Vector diagram of a voltage in the complex plane

In a vector diagram , a harmonic oscillation (sinusoidal oscillation) can be represented in the complex plane by a pointer rotating at the angular frequency around the zero point , the length of which represents the amplitude. This makes a transition from a function of time to a function of the angle, which in this context is called the phase angle . This increases accordingly . The pointer rotates counterclockwise to match the counting direction of the angle. It is also called the rotary pointer. The time course of the oscillation can be obtained by projecting the rotating pointer tip onto the imaginary axis (sine function) or the real axis (cosine function). ${\displaystyle \omega }$ ${\displaystyle \varphi }$ ${\displaystyle \varphi =\omega t+\varphi _{0}}$

A rotating pointer for the voltage or can be represented by a complex voltage , which is defined as follows: ${\displaystyle u={\hat {u}}\cdot \cos(\omega t+\varphi _{u})}$ ${\displaystyle u={\hat {u}}\cdot \sin(\omega t+\varphi _{u})}$

${\displaystyle {\underline {u}}={\hat {u}}\cdot (\cos(\omega t+\varphi _{u})+\mathrm {j} \cdot \sin(\omega t+\varphi _{u}))={\hat {u}}\cdot \mathrm {e} ^{\mathrm {j} (\omega t+\varphi _{u})}={\hat {u}}\,{\big /}\!\!\!{\underline {\;\,\omega t+\varphi _{u}}}}$

The last expression represents the so-called default notation . As in the penultimate expression, the complex quantity is specified in polar coordinates .

Example: The formula speaks itself: is equal to supply , where the amount and the argument are the complex quantity . ${\displaystyle {\underline {c}}=a{\big /}\!\!\!{\underline {\,\,\varphi }}}$ ${\displaystyle c}$ ${\displaystyle a}$ ${\displaystyle \varphi }$ ${\displaystyle a}$ ${\displaystyle \varphi }$ ${\displaystyle {\underline {c}}}$

Analogously, one defines for the current or the complex current strength : ${\displaystyle i={\hat {i}}\cdot \cos(\omega t+\varphi _{i})}$ ${\displaystyle i={\hat {i}}\cdot \sin(\omega t+\varphi _{i})}$

${\displaystyle {\underline {i}}={\hat {\imath }}\cdot (\cos(\omega t+\varphi _{i})+\mathrm {j} \cdot \sin(\omega t+\varphi _{i}))={\hat {\imath }}\cdot \mathrm {e} ^{\mathrm {j} (\omega t+\varphi _{i})}={\hat {\imath }}\,{\big /}\!\!\!{\underline {\;\,\omega t+\varphi _{i}}}}$

Depending on whether the cosine or the sine is preferably used to describe all signals, the real quantities can be represented as real parts or imaginary parts of the complex quantities. Alternatively, the real quantities can also be determined by adding or subtracting the conjugate complex signals:

${\displaystyle u=\operatorname {Re} \ {\underline {u}}={\frac {{\underline {u}}+{\underline {u}}^{*}}{2}}}$

${\displaystyle i=\operatorname {Re} \ {\underline {i}}={\frac {{\underline {i}}+{\underline {i}}^{*}}{2}}}$

or.

${\displaystyle u=\operatorname {Im} \ {\underline {u}}={\frac {{\underline {u}}-{\underline {u}}^{*}}{2\mathrm {j} }}}$

${\displaystyle i=\operatorname {Im} \ {\underline {i}}={\frac {{\underline {i}}-{\underline {i}}^{*}}{2\mathrm {j} }}}$

The representation on the basis of the conjugate complex signals enables the interpretation of the real signal as a superposition of a (counterclockwise) rotating pointer - the complex signal - and a pointer rotating in the opposite direction (clockwise) - the conjugate complex signal.

Complex amplitudes and complex rms values

The definition of complex amplitudes ( phasors ) (initially used as an abbreviation) is essential for the complex calculation.

${\displaystyle {\underline {\hat {U}}}={\hat {u}}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{u}}={\hat {u}}{\big /}\!\!\!{\underline {\,\,\varphi _{u}}}}$

and

${\displaystyle {\underline {\hat {I}}}={\hat {\imath }}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{i}}={\hat {\imath }}{\big /}\!\!\!{\underline {\,\,\varphi _{i}}}}$

or alternatively of complex effective values

${\displaystyle {\underline {U}}={\frac {\hat {u}}{\sqrt {2}}}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{u}}=U\cdot \mathrm {e} ^{\mathrm {j} \varphi _{u}}=U{\big /}\!\!\!{\underline {\,\,\varphi _{u}}}}$

and

${\displaystyle {\underline {I}}={\frac {\hat {\imath }}{\sqrt {2}}}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{i}}=I\cdot \mathrm {e} ^{\mathrm {j} \varphi _{i}}=I{\big /}\!\!\!{\underline {\,\,\varphi _{i}}}}$

from the (real) amplitudes or effective values ​​and the zero phase angles.

This means that the complex instantaneous values ​​can be written as

${\displaystyle {\underline {u}}={\sqrt {2}}\cdot {\underline {U}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}={\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}$

and

${\displaystyle {\underline {i}}={\sqrt {2}}\cdot {\underline {I}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}={\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}$

Since the complex amplitudes and the complex rms values ​​do not depend on time, they correspond to stationary pointers for representing a sinusoidal signal. They combine the two real constants, amplitude or rms value and the zero phase angle, to form a complex, time-independent constant. By multiplying with the harmonic exponential , which represents a rotating unit pointer, the complex voltage or the complex current is created again. This factor occurs uniformly in every complex signal in the entire system. With the help of the complex amplitudes, the real signals can finally be written as follows: ${\displaystyle \mathrm {e} ^{\mathrm {j} \omega t}}$

${\displaystyle u=\operatorname {Re} \left({\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}\right)={\frac {1}{2}}\cdot \left({\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}+{\underline {\hat {U}}}^{*}\cdot \mathrm {e} ^{-\mathrm {j} \omega t}\right)}$

${\displaystyle i=\operatorname {Re} \left({\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}\right)={\frac {1}{2}}\cdot \left({\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}+{\underline {\hat {I}}}^{*}\cdot \mathrm {e} ^{-\mathrm {j} \omega t}\right)}$

or.

${\displaystyle u=\operatorname {Im} \left({\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}\right)={\frac {1}{2\mathrm {j} }}\cdot \left({\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}-{\underline {\hat {U}}}^{*}\cdot \mathrm {e} ^{-\mathrm {j} \omega t}\right)}$

${\displaystyle i=\operatorname {Im} \left({\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}\right)={\frac {1}{2\mathrm {j} }}\cdot \left({\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}-{\underline {\hat {I}}}^{*}\cdot \mathrm {e} ^{-\mathrm {j} \omega t}\right)}$

Because of the superposition theorem that applies by definition, it is sufficient to carry out all calculations only with the complex signals and to use the real or imaginary part of the result at the end. This applies to addition and subtraction, to multiplication with real constants and to differentiation and integration, but not to multiplication or division of signals. Computing with complex signals is generally easier than computing with real sinusoidal signals.

It turns out that in all calculations the angular frequency is always associated with the imaginary unit . This is why the term imaginary frequency is still used in the literature (to distinguish it from the complex frequency ) . If the value range of is extended by “ negative frequencies ” from to , then this negative semiaxis of the frequency is “covered” by the second (complex conjugate) term. A real sinusoidal signal of the angular frequency therefore always consists of a pair of complex signals with the imaginary frequencies and . ${\displaystyle \omega }$ ${\displaystyle \mathrm {j} }$ ${\displaystyle \mathrm {j} \omega }$ ${\displaystyle \omega }$ ${\displaystyle -\infty }$ ${\displaystyle +\infty }$ ${\displaystyle \omega }$ ${\displaystyle \mathrm {j} \omega }$ ${\displaystyle -\mathrm {j} \omega }$

The purely imaginary expression also turns out to be a differential operator , because it applies, for example, to the time derivative of the complex voltage ${\displaystyle \mathrm {j} \omega }$

${\displaystyle {\frac {d{\underline {u}}(t)}{dt}}={\frac {d}{dt}}({\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t})={\underline {\hat {U}}}\cdot {\frac {d}{dt}}(\mathrm {e} ^{\mathrm {j} \omega t})={\underline {\hat {U}}}\cdot \mathrm {j} \omega \cdot \mathrm {e} ^{\mathrm {j} \omega t}=\mathrm {j} \omega \cdot ({\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t})=\mathrm {j} \omega \cdot {\underline {u}}(t)}$

Because the “complicated” differential operator is replaced by a simple multiplication with , differential equations become algebraic equations that are much easier to solve. ${\displaystyle {\frac {d}{dt}}}$ ${\displaystyle \mathrm {j} \omega }$

Ohm's law in the complex domain

Complex resistance

Vector diagram of a resistor

While the ratio of a sinusoidal voltage to a sinusoidal current only gives a time-independent value at an ohmic resistor , it is generally time-dependent and therefore does not represent a practically usable quantity for describing a two-pole . In contrast, the ratio of a complex voltage to a complex current intensity is on a complex, time-independent constant for every linear two-pole, because the harmonic exponential , which is contained as a factor in every complex signal , is canceled out . This statement is sometimes called Ohm's Law of Alternating Current Engineering. The constant is called a complex resistance , impedance, or resistance operator: ${\displaystyle {\frac {u(t)}{i(t)}}}$ ${\displaystyle {\frac {{\underline {u}}(t)}{{\underline {i}}(t)}}}$ ${\displaystyle \mathrm {e} ^{\mathrm {j} \omega t}}$ ${\displaystyle {\underline {Z}}}$

${\displaystyle {\underline {Z}}={\frac {\underline {u}}{\underline {i}}}={\frac {{\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}{{\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}}={\frac {\underline {\hat {U}}}{\underline {\hat {I}}}}={\frac {\underline {U}}{\underline {I}}}={\frac {{\hat {u}}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{u}}}{{\hat {\imath }}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{i}}}}={\frac {\hat {u}}{\hat {\imath }}}\cdot \mathrm {e} ^{\mathrm {j} (\varphi _{u}-\varphi _{i})}}$

The impedance can also be calculated as the ratio of the complex amplitudes or the complex rms values ​​of voltage and current. Like this, the impedance in the complex plane can be represented as a pointer at rest. It will generally depend on the angular frequency . It can be broken down into the real part , which is called real resistance or resistance, and the imaginary part , which is called reactance or reactance: ${\displaystyle \omega }$ ${\displaystyle R}$ ${\displaystyle X}$

${\displaystyle {\underline {Z}}=R+\mathrm {j} X}$

The reciprocal of the impedance is called complex conductance , admittance or conductance operator : ${\displaystyle {\underline {Y}}}$

${\displaystyle {\underline {Y}}={\frac {1}{\underline {Z}}}={\frac {\underline {i}}{\underline {u}}}={\frac {{\underline {\hat {I}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}{{\underline {\hat {U}}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}}={\frac {\underline {\hat {I}}}{\underline {\hat {U}}}}={\frac {\underline {I}}{\underline {U}}}={\frac {{\hat {\imath }}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{i}}}{{\hat {u}}\cdot \mathrm {e} ^{\mathrm {j} \varphi _{u}}}}={\frac {\hat {\imath }}{\hat {u}}}\cdot \mathrm {e} ^{\mathrm {j} (\varphi _{i}-\varphi _{u})}}$

The admittance is in the real part , the one conductance calls or conductance and the imaginary , the one susceptance or susceptance called, are broken down: ${\displaystyle G}$ ${\displaystyle B}$

${\displaystyle {\underline {Y}}=G+\mathrm {j} B}$

Ohmic resistance

If the equation for ohmic resistance in the introduction above is used instead of and pointers, the result is ${\displaystyle R}$ ${\displaystyle u}$ ${\displaystyle i}$

${\displaystyle {\frac {\underline {u}}{\underline {i}}}=R}$

Since it is a real quantity, the general approach must be to look at the angles ${\displaystyle R}$

${\displaystyle \varphi _{u}-\varphi _{i}\,=0}$

be. The pointers and always have the same zero phase angle at the ohmic resistor. This corresponds to the observation that and are in phase. The complex resistance is then: ${\displaystyle {\underline {u}}}$ ${\displaystyle {\underline {i}}}$ ${\displaystyle {\underline {u}}}$ ${\displaystyle {\underline {i}}}$

${\displaystyle {\underline {Z}}_{R}=R={\frac {\underline {u}}{\underline {i}}}={\frac {\underline {\hat {U}}}{\underline {\hat {I}}}}={\frac {\hat {u}}{\hat {\imath }}}{\big /}\!\!\!{\underline {\;\;0_{\,}}}={\frac {\hat {u}}{\hat {\imath }}}}$

capacitor

If pointers are substituted for and in the above equation for the capacitance , the differentiation occurs after execution ${\displaystyle C}$ ${\displaystyle u}$ ${\displaystyle i}$

${\displaystyle {\frac {\underline {i}}{C}}={\frac {\mathrm {d} {\underline {u}}}{\mathrm {d} t}}={\hat {u}}\cdot \mathrm {e} ^{\mathrm {j} (\omega t+\varphi _{u})}\cdot \mathrm {j} \omega ={\underline {u}}\ \mathrm {j} \omega }$

After conversion and with

${\displaystyle \mathrm {e} ^{-\mathrm {j} {\frac {\mathrm {\pi } }{2}}}=\cos \left(-{\frac {\mathrm {\pi } }{2}}\right)+\mathrm {j} \sin \left(-{\frac {\mathrm {\pi } }{2}}\right)=0+\mathrm {j} \cdot (-1)=-\mathrm {j} }$

surrendered

${\displaystyle {\frac {\underline {u}}{\underline {i}}}={\frac {1}{\mathrm {j} \omega C}}=-\mathrm {j} \cdot {\frac {1}{\omega C}}={\frac {1}{\omega C}}\cdot \mathrm {e} ^{-\mathrm {j} {\frac {\mathrm {\pi } }{2}}}}$

Then the general approach must be in looking at the angles

${\displaystyle \varphi _{u}-\varphi _{i}=-{\frac {\mathrm {\pi } }{2}}}$

be. This corresponds to the observation that in the case of an ideal capacitor , the phase is shifted by −π / 2 or −90 °. The impedance is then ${\displaystyle {\underline {u}}}$ ${\displaystyle {\underline {i}}}$

Impedance of a capacitor ${\displaystyle C=1\;\mathrm {\mu F} }$

${\displaystyle {\underline {Z}}_{C}={\frac {1}{\mathrm {j} \omega C}}=\mathrm {j} \cdot X_{C}={\frac {\underline {u}}{\underline {i}}}={\frac {\underline {\hat {U}}}{\underline {\hat {I}}}}={\frac {\hat {u}}{\hat {\imath }}}{\big /}\!\!\!{\underline {\;\;-90_{\,}^{\circ }}}}$

With regard to the real and imaginary part, the complex resistance here only consists of a negative imaginary part. This provides a negative reactance for the capacitor ${\displaystyle {\underline {Z}}_{C}}$

${\displaystyle X_{C}=-{\frac {1}{\omega \cdot C}}=-{\frac {1}{2\mathrm {\pi } f\cdot C}}}$

The complex resistance of a capacitor is thus plotted on the imaginary axis in the negative direction. The formula shows that the reactance of the capacitor becomes smaller the higher the frequency is selected.

Kitchen sink

If pointers are used in the above equation for inductance instead of and , the differentiation occurs after execution ${\displaystyle L}$ ${\displaystyle u}$ ${\displaystyle i}$

${\displaystyle {\frac {\underline {u}}{L}}={\frac {\mathrm {d} {\underline {i}}}{\mathrm {d} t}}={\hat {\imath }}\cdot \mathrm {e} ^{\mathrm {j} (\omega t+\varphi _{i})}\cdot \mathrm {j} \omega ={\underline {i}}\ \mathrm {j} \omega }$

After conversion and with

${\displaystyle \mathrm {e} ^{\mathrm {j} {\frac {\mathrm {\pi } }{2}}}=\cos \left({\frac {\mathrm {\pi } }{2}}\right)+\mathrm {j} \sin \left({\frac {\mathrm {\pi } }{2}}\right)=\mathrm {j} }$

surrendered

${\displaystyle {\frac {\underline {u}}{\underline {i}}}=\mathrm {j} \cdot \omega L=\omega L\cdot \mathrm {e} ^{\mathrm {j} {\frac {\mathrm {\pi } }{2}}}}$

Then the general approach must be in looking at the angles

${\displaystyle \varphi _{u}-\varphi _{i}={\frac {\mathrm {\pi } }{2}}}$

be. This corresponds to the observation that in the case of an ideal coil against advanced by π / 2 or 90 °. The impedance is then ${\displaystyle {\underline {u}}}$ ${\displaystyle {\underline {i}}}$

Impedance of a coil ${\displaystyle L=1\;\mathrm {mH} }$

${\displaystyle {\underline {Z}}_{L}=\mathrm {j} \omega L=\mathrm {j} \cdot X_{L}={\frac {\underline {u}}{\underline {i}}}={\frac {\underline {\hat {U}}}{\underline {\hat {I}}}}={\frac {\hat {u}}{\hat {\imath }}}{\big /}\!\!\!{\underline {\;\;90_{\,}^{\circ }}}}$

With regard to the real and imaginary part, the complex resistance here consists only of a positive imaginary part. This provides a positive reactance for the coil ${\displaystyle {\underline {Z}}_{L}}$

${\displaystyle X_{L}=\omega \cdot L=2\pi f\cdot L}$

As with the capacitor, the complex resistance of the coil is now on the imaginary axis. However, unlike the capacitor, it is applied in a positive direction. The reactance of the inductance also increases with increasing frequency, in contrast to the capacitor. In a series connection of a coil and capacitor, these opposing properties lead to the reactance of a certain type adding to zero, which is known as series resonance in the resonant circuit . ${\displaystyle {\underline {Z}}_{L}}$ ${\displaystyle \omega >0}$

The symbolic method

Solution program

As shown above, with the help of the complex voltages and currents, the property of as a differential operator and the defined impedances and admittances, the network differential equations can be transformed into algebraic equations and thus solved more easily. ${\displaystyle \mathrm {j} \omega }$

The “actual” symbolic method of the complex AC calculation goes one step further. Without first setting up the network differential equation, the circuit diagram is already "transformed into the complex". This becomes clear in the following solution program :

1. In the circuit diagram, all (steady-state sinusoidal) voltages and currents are replaced by their (time-independent) complex amplitudes or rms values.
2. In the circuit diagram, all (linear) two-pole equations of the components are replaced by their impedances or admittances. This is obtained by replacing the (possibly existing) differential operator with . ${\displaystyle \mathrm {j} \omega }$
3. The (algebraic) system of equations of the network is set up. In addition to the basic rules of direct current technology ( Kirchhoff's rules , Ohm's law , series connection , parallel connection , voltage divider rule , current divider rule ), the simplified analysis methods for linear networks are used.
4. The calculation of the complex amplitudes or effective values ​​of the quantities sought by solving the algebraic system of equations is carried out using the known mathematical methods for linear systems of equations . In practice, the determined complex amplitudes or effective values ​​are sufficiently meaningful (e.g. as a vector diagram or in locus curves ). The representation in exponential notation allows the direct reading of real amplitudes and zero phases, so that the calculation can end here.
5. If necessary, the determined complex amplitudes or rms values ​​can be "back transformed" into the real signals by multiplying with or and then real or imaginary parts. ${\displaystyle \mathrm {e} ^{\mathrm {j} \omega t}}$ ${\displaystyle {\sqrt {2}}\cdot \mathrm {e} ^{\mathrm {j} \omega t}}$

With the help of this symbolic method of the complex AC calculation, the calculation of AC networks is reduced to the methods of DC networks, but not necessarily to their simplicity.

Some authors speak of a transformation of the sinusoidal signals of the time domain into the complex amplitudes of the frequency domain with the symbolic method of the complex alternating current calculation , based on other operator calculations . This can be illustrated clearly using the Fourier transformation. The Fourier transformation of a voltage in the original domain (time domain) results, with appropriate normalization, ${\displaystyle u}$

${\displaystyle {\begin{aligned}&{{\underline {c}}_{n}}={\frac {2}{T}}\int \limits _{T}{{\hat {u}}\cos(\omega t+{{\varphi }_{u}})\,{{\text{e}}^{-{\text{j}}n\omega t}}{\text{d}}t}\\&={\frac {\hat {u}}{T}}\int \limits _{T}{({{e}^{{\text{j}}(\omega t+{{\varphi }_{u}})}}+{{e}^{-{\text{j}}(\omega t+{{\varphi }_{u}})}})\,{{\text{e}}^{-{\text{j}}n\omega t}}{\text{d}}t}\\&{{\underline {c}}_{n=1}}={\underline {\hat {U}}}={\underline {U}}{\sqrt {2}}\end{aligned}}}$

precisely the complex amplitude or the complex effective value in the image area (frequency area). The Fourier coefficients thus correspond precisely to the resting complex vectors or . The Fourier transformation can therefore be understood as a formal rule of how the time-dependent real currents and voltages are transformed into the complex description and back again. ${\displaystyle {{\underline {c}}_{n}}}$ ${\displaystyle {\underline {U}}}$ ${\displaystyle {\underline {\hat {U}}}}$

The advantage of this mutual assignment and the use of the symbolic method of the complex alternating current calculation has been shown by "long-term use" in the practice of alternating current and high-frequency circuits.

Example for the solution program

The procedure is to be demonstrated using the example of a low pass :

Circuit diagram of a low-pass filter in the area of ​​the complex AC calculation

Given the generator voltage and all values ​​of the components, the voltage across the load resistor is sought . Both are labeled as complex rms values from the start . The components are also characterized by their (complex) impedances. The solution can be written down immediately based on the rules for series and parallel connections as well as the voltage divider rule: ${\displaystyle {\underline {U}}_{G}}$ ${\displaystyle {\underline {U}}_{R_{L}}}$ ${\displaystyle R_{L}}$

${\displaystyle {\underline {U}}_{R_{L}}={\underline {U}}_{G}\cdot {\frac {R_{L}\parallel {\frac {1}{\mathrm {j} \omega C}}}{R_{G}+\mathrm {j} \omega L+R_{L}\parallel {\frac {1}{\mathrm {j} \omega C}}}}}$

We divide the numerator and denominator ${\displaystyle R_{L}\parallel {\frac {1}{\mathrm {j} \omega C}}}$

${\displaystyle {\underline {U}}_{R_{L}}={\underline {U}}_{G}\cdot {\frac {1}{{\frac {R_{G}+\mathrm {j} \omega L}{R_{L}\parallel {\frac {1}{\mathrm {j} \omega C}}}}+1}}}$

and reduce the double fraction with ${\displaystyle {\frac {1}{R_{L}\parallel {\frac {1}{\mathrm {j} \omega C}}}}={\frac {1}{R_{L}}}+\mathrm {j} \omega C}$

${\displaystyle {\underline {U}}_{R_{L}}={\underline {U}}_{G}\cdot {\frac {1}{\left(R_{G}+\mathrm {j} \omega L\right)\cdot \left({\frac {1}{R_{L}}}+\mathrm {j} \omega C\right)+1}}}$

and finally get the desired transmission behavior in the frequency domain with a denominator arranged according to real and imaginary part:

${\displaystyle {\underline {U}}_{R_{L}}={\frac {{\underline {U}}_{G}}{1+{\frac {R_{G}}{R_{L}}}-\omega ^{2}\cdot L\cdot C+\mathrm {j} \omega \cdot \left({\frac {L}{R_{L}}}+R_{G}\cdot C\right)}}}$

The result can be normalized for further evaluation and displayed graphically as a locus. Alternatively, you can convert it to exponential notation and read off the frequency response of amplitude and phase separately and, if necessary, display it graphically:

${\displaystyle {\frac {{\underline {U}}_{R_{L}}}{{\underline {U}}_{G}}}={\frac {1}{\sqrt {\left(1+{\frac {R_{G}}{R_{L}}}-\omega ^{2}\cdot L\cdot C\right)^{2}+\omega ^{2}\cdot \left({\frac {L}{R_{L}}}+R_{G}\cdot C\right)^{2}}}}\cdot \exp \left(-\mathrm {j} \arctan {\frac {\omega \cdot \left({\frac {L}{R_{L}}}+R_{G}\cdot C\right)}{1+{\frac {R_{G}}{R_{L}}}-\omega ^{2}\cdot L\cdot C}}\right)}$

The classic solution of this example with the help of differential equations would have come to the same result, but would have required a multiple of more complicated computing effort.

Rules for the representation of the pointer

The rules on parallel connection and series connection as well as the Kirchhoff rules continue to apply unchanged in AC technology when they are applied to complex quantities. First of all, it is determined from which size it is appropriate to assume. It often proves to be useful to place this quantity in the real axis.

If all components are connected in series, it is useful to specify the current. For each element through which the same current flows, the applied voltage can be determined and then all voltages can be summarized by adding the phasors. Equivalently, all resistances can first be complexly added and then multiplied by the current.

However, if all components are connected in parallel, a voltage is specified. The current can be calculated separately for each element and then all complex currents can be added by stringing the pointers together. Equivalently, all complex conductance values ​​can first be added and then multiplied by the voltage.

If the circuit is a mixed form, it should be broken down elementarily and each sub-circuit calculated separately before everything is put back together. An example is described in Resonance Transformer.

Pointer in the complex plane for an RC series circuit:
above: alternating current and voltage,
below: alternating current resistances

Example of the pointer display

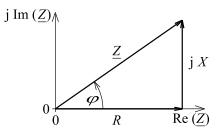
An alternating voltage is also applied to a series connection of a resistor and a capacitor . ${\displaystyle R=150\,\Omega }$ ${\displaystyle C=10\,\mu \mathrm {F} }$ ${\displaystyle \omega =500\,\mathrm {s} ^{-1}}$

It has an effective resistance

${\displaystyle R=150\,\Omega }$

and a reactance

${\displaystyle X_{C}=-\,{\frac {1}{\omega C}}=-\,{\frac {1}{500\ \mathrm {s} ^{-1}\cdot 10^{-5}\ \mathrm {F} }}=-\,200\,\Omega }$

with the conversion of the units of measurement ${\displaystyle \mathrm {F} =\mathrm {A} \cdot \mathrm {s} \,/\,\mathrm {V} =\mathrm {s} \,/\,\Omega \,,}$

which add up to the total impedance as complex quantities when connected in series

${\displaystyle {\underline {Z}}={\underline {Z}}_{R}+{\underline {Z}}_{C}=R+\mathrm {j} X_{C}=150\,\Omega -\mathrm {j} \,200\,\Omega \,.}$

The impedance (magnitude of the impedance) is obtained according to the Pythagorean theorem to

${\displaystyle {\begin{aligned}Z&=|{\underline {Z}}|={\sqrt {(\operatorname {Re} \{{\underline {Z}}\})^{2}+(\operatorname {Im} \{{\underline {Z}}\})^{2}}}\\&={\sqrt {(150\,\Omega )^{2}+(200\,\Omega )^{2}}}=250\,\Omega \,.\end{aligned}}}$

So it is the ratio of the amounts of voltage and current. For the phase shift angle φ between voltage and current in this circuit it follows:

${\displaystyle \varphi =\arctan {\frac {\operatorname {Im} \{{\underline {Z}}\}}{\operatorname {Re} \{{\underline {Z}}\}}}=\arctan {\frac {-200\,\Omega }{150\,\Omega }}=-53{,}13^{\circ }\,.}$

This enables the notation in polar coordinates: ${\displaystyle {\underline {Z}}=250\,\Omega \cdot \mathrm {e} ^{-\mathrm {j} \,53{,}13^{\circ }}=250\,\Omega \,{\big /}\!\!\!{\underline {\;-53{,}13^{\circ }}}\,.}$

Complex invoice performance

→ Main article : Complex performance (electrical engineering)

In the product of a complex voltage and a conjugate complex current, the time-dependent parts and cancel each other out and only the mutual phase shift is included . The resulting time-independent pointer, which is compatible with the complex AC calculation, is referred to as complex power or complex apparent power . ${\displaystyle \mathrm {e} ^{\mathrm {j} \omega t}}$ ${\displaystyle \mathrm {e} ^{-\mathrm {j} \omega t}}$

${\displaystyle {\underline {S}}={\underline {U}}\ {\underline {I}}^{\star }=S\;\mathrm {e} ^{\mathrm {j} (\varphi _{u}-\varphi _{i})}=P+\mathrm {j} Q}$

This includes the three performance parameters commonly used in AC technology:

• the apparent power ${\displaystyle S}$

${\displaystyle S=\left|{\underline {S}}\right|=U\;I}$

• the real power , which is defined as an equivalent over ; the vibration component drops out due to the averaging. It turns out ${\displaystyle P}$ ${\displaystyle p}$

${\displaystyle P=\mathrm {Re} \ {\underline {S}}=U\;I\;\cos(\varphi _{u}-\varphi _{i})}$

• the (displacement) reactive power, which is also free from vibration components (instantaneous values) ${\displaystyle Q}$

${\displaystyle Q=\mathrm {Im} \ {\underline {S}}=U\;I\;\sin(\varphi _{u}-\varphi _{i})}$

Application and generalization

In addition to the analysis of classic alternating current networks of high and low current technology, the complex alternating current calculation is an indispensable prerequisite for the following areas of linear electrical engineering and linear analog electronics:

• Representation of the network behavior in loci
• Calculations of resonance circles
• Calculations on the transformer
• Theory of two goals
• Calculations of filters (e.g. of two-circuit band filters )
• Calculation of the current and river displacement
• Transmission line theory ( line theory )
• Calculation of the propagation of electromagnetic waves in space

Shortly after its publication, attempts were made to generalize the complex AC calculation. This has happened in several directions over time:

• The application of the complex Fourier series in electrical engineering made it possible to use the impedance functions for non-sinusoidal periodic signals.
• The expanded symbolic method enabled the better investigation of impedance functions in the pole-zero diagram and laid the foundations for the theory of network and filter synthesis by introducing the complex frequency due to the generalization of the complex alternating current calculation to exponentially increasing and decreasing sinusoidal signals .
• Soon an attempt was made to use a symbolic method for non-periodic signals as well. The operator calculation according to Heaviside arose , but only the Fourier and Laplace transformation (in their various forms) brought the breakthrough here. The operator calculation according to Mikusiński enabled a purely algebraic justification of these methods.
• Such a justification was also worked out as an AC calculus, which dispenses with the introduction of complex-valued time functions, as an alternative to the complex alternating current calculation.

With regard to this list, it should also be noted that the impedance and admittance functions of the complex AC calculation can continue to be used almost unchanged in all of the generalizations mentioned.

literature

• Klaus Lunze : Theory of AC circuits . 8th edition. Verlag Technik GmbH, Berlin 1991, ISBN 3-341-00984-1 .
• Reinhold Paul: Electrical engineering 2 - networks . Springer-Verlag, Berlin Heidelberg New York 1994, ISBN 3-540-55866-7 .
• Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretical electrical engineering . 18th edition. Springer, 2008, ISBN 978-3-540-78589-7 .

Individual evidence

1. ↑ Charles P. Steinmetz: The application of complex quantities in electrical engineering . No. 14 .. Elektrotechnische Zeitung (ETZ), 1893.
2. ^ Wilhelm Quade: Mathematical justification of the complex alternating current calculation . No. 2 . German Mathematicians Association (DMV), 1937, p. 18-31 .
3. ↑ DIN 5483-2: 1982 Time- dependent quantities - Part 2: Formula symbols , chap. 1.5
4. ↑ DIN EN 60027-1: 2007 Symbols for electrical engineering - Part 1: General , chap. 2.2.4
5. ↑ ^{a b c} DIN 5483-3: 1994 Time-dependent quantities - Part 3: Complex representation of sinusoidal time-dependent quantities
6. ↑ DIN 1304-1: 1994 Formula symbols - Part 1: General formula symbols
7. ↑ DIN 1302 : 1999 General mathematical symbols and terms
8. ↑ ^{a b} DIN 40 110-1: 1994 alternating currents - part 1: two-wire circuits
9. ↑ Gerhard Wunsch : History of Systems Theory (=  Scientific Pocket Books: Texts and Studies . Volume 296 ). Akademie-Verlag, Leipzig 1985, DNB  850752914 .
10. ↑ Wolfgang Mathis: Theory of nonlinear networks . Springer, 1987, ISBN 978-3-540-18365-5 .