Low pass

Low pass filter: circuit symbol

As low pass is called in the electronics such filters , the signal components with frequencies below its cutoff frequency can pass almost unattenuated, components with higher frequencies attenuate it. Corresponding filter functions can also occur in other areas, such as mechanics , acoustics or hydraulics , but they are usually not called that there. Any kind of mechanical inertia also has a low-pass effect. Associated with the attenuation is a time delay which shifts the phase angle in the case of a sinusoidal signal curve .

application

Low-pass filters in electronics are often passive analog low-pass filters that consist of resistors , coils and capacitors . With additional active components such as operational amplifiers or transistors , can active analog low-pass filters can be realized.

In digital signal processing , time-discrete low-pass filters are implemented in filter structures such as the FIR or IIR filter . This is done with digital circuits such as FPGAs or by means of sequential computer programs .

Low-pass filters for high power for high frequency and electrical power engineering are made up of capacitors and coils. They can be found at the load outputs of frequency converters , class D amplifiers , switched-mode power supplies and in line filters .

Low-pass filter in audio technology are also called high barrier , high pass filter , Treble cut filter , high-cut filter , or noise filter called. These terms used in sound engineering indicate that such a filter, for example in an equalizer , attenuates the "highs" of the signal or noise containing high frequencies; see also equalization (sound engineering) . LC low-pass filters are connected upstream of the woofers in loudspeaker boxes.

Low-pass properties are also found in mechanics (vibration damping), acoustics (the sound propagation of lower frequencies is less lossy), optics (edge ​​filters), hydraulics or the propagation of light in the atmosphere, but are not called that there.

In measurement technology , the low-pass is also referred to as an arithmetic mean value image, e.g. B. behaves like a moving coil measuring mechanism . When generating a variable DC voltage using PWM demodulation , a downstream low-pass filter is required in order to suppress the PWM frequency.

An ideal low-pass filter has a non- causal transfer function and therefore cannot be implemented. It is only valid as a simplified model in filter theory. Real low-pass filters can only approximate the property of an ideal low-pass filter as closely as possible.

presentation

The general mathematical approach for a filter leads to a differential equation . Especially for sinusoidal quantities, the solution can be simplified by using complex-valued quantities, see complex alternating current calculation .

The frequency and phase response fully describe the behavior of a filter. These curves are represented by the complex voltage ratio H = U _a / U _e (or by the gain A (w) = 20 log ₁₀ | H (w) |) and the phase shift angle φ between U _a and U _e in a Bode- Diagram or by means of a locus .

1st order low pass

Voltage V _C across the capacitance as a function of time with a sudden change in the input voltage

description

Frequency response of a passive first-order low-pass filter with a sinusoidal input voltage, shown as a Bode diagram, = voltage ratio , = phase shift angle, intended for
${\displaystyle A}$ ${\displaystyle U_{a}/U_{e}}$
${\displaystyle \varphi }$
${\displaystyle RC=0{,}1\,\mathrm {s} }$

In the simplest case, a low-pass filter consists of a resistor - capacitor combination ( RC element ) and represents a Butterworth filter with 1st order in the following arrangement:

It is assumed that the source impedance of U _{e is} zero and the load impedance of U _{a is} infinitely high.

A sudden change in the input voltage U _{e is} followed by the output voltage U _a by the same amount of jump, but with a delay in the course of an exponential function with a time constant τ = RC .

A sinusoidal input voltage with the frequency f is followed at the output by a sinusoidal voltage that is attenuated as a function of the frequency according to the voltage divider rule because of the linear properties of the components

${\displaystyle U_{a}=U_{e}\cdot {\frac {\vert X_{C}\vert }{\sqrt {R^{2}+X_{C}^{2}}}}={\frac {U_{e}}{\sqrt {1+(\omega CR)^{2}}}}}$

where and denote the amounts of the output and input voltage, the amount of the reactance of the capacitor and the angular frequency . ${\displaystyle U_{a}\ }$ ${\displaystyle U_{e}\ }$ ${\displaystyle |X_{C}|={\frac {1}{\omega C}}}$ ${\displaystyle \omega =2\pi f}$

Low pass: locus

In the logarithmic representation over the frequency (Bode diagram) the division ratio has two asymptotes . At low frequencies it goes towards 1 and for DC voltage (frequency f  = 0) it becomes . At high frequencies it decreases by 6 dB / octave or 20 dB / decade. The cutoff frequency f _c is the frequency at which the asymptotes intersect. Here is ${\displaystyle U_{a}=U_{e}\ }$

${\displaystyle U_{a}=U_{e}/{\sqrt {2}}\approx U_{e}\cdot 0{,}707}$

(i.e. U _a is attenuated by 3 dB compared to U _e ). The cutoff frequency is ${\displaystyle f_{c}={\frac {1}{2\pi RC}}}$

If the frequency deviates from the limit frequency by more than a power of ten (upwards or downwards), the curve with a relative deviation of less than ½% can be replaced by the respective asymptote.

Active inverting low-pass 1st order

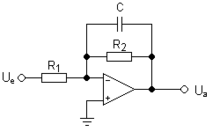
Active low-pass filters can be implemented with operational amplifiers . These have the advantage that the frequency response is retained even with a load connected to the output. They can also be dimensioned in such a way that they only load the source minimally, so that it can have an impedance greater than zero. The amount of the output voltage of this low-pass filter is

${\displaystyle U_{a}=-U_{e}\cdot {\frac {R_{2}}{R_{1}}}\cdot {\frac {\vert X_{C}\vert }{\sqrt {X_{C}^{2}+R_{2}^{2}}}}\ }$

At the cut-off frequency , the gain has fallen correspondingly to -fold the DC voltage gain , which is (apart from the sign reversal) . ${\displaystyle f_{c}=1/(2\pi R_{2}C)}$ ${\displaystyle {\sqrt {\tfrac {1}{2}}}}$ ${\displaystyle R_{2}/R_{1}}$

Derivation of the formula

In the representation of the alternating quantities by complex quantities, the following applies to the voltage ratio according to the voltage divider rule :

${\displaystyle {\underline {H}}={\frac {\underline {U_{a}}}{\underline {U_{e}}}}={\frac {\underline {Z_{c}}}{{\underline {Z_{c}}}+R}}={\frac {\frac {1}{\mathrm {j} \omega C}}{{\frac {1}{\mathrm {j} \omega C}}+R}}={\frac {1}{1+\mathrm {j} \omega CR}}\quad }$

with = resistance operator or impedance of the capacitor. ${\displaystyle {\underline {Z_{c}}}={\frac {1}{{\mathrm {j} }{\omega }{C}}}}$

With an auxiliary variable

${\displaystyle {\underline {z}}=x+\mathrm {j} y=1+\mathrm {j} \omega CR}$

${\displaystyle {\underline {z}}=z\,\mathrm {e} ^{\mathrm {j} \varphi }\quad \Rightarrow \quad z={\sqrt {x^{2}+y^{2}}}\quad {\text{und}}\quad \varphi =\arctan \left({\frac {y}{x}}\right)}$

${\displaystyle {\underline {z}}={\sqrt {1+(\omega CR)^{2}}}\cdot \mathrm {e} ^{\mathrm {j} \cdot \arctan(\omega CR)}}$

you get

${\displaystyle {\underline {H}}={\frac {1}{\underline {z}}}={\frac {1}{\sqrt {1+(\omega CR)^{2}}}}\cdot \mathrm {e} ^{-\mathrm {j} \cdot \arctan {(\omega CR)}}}$

This equation represents the locus curve for the complex voltage transfer function.

Inferences

From this we derive:

Amounts

The formula given above results from the transition to amounts and reactance (real values)

${\displaystyle {\begin{aligned}H&={\frac {1}{\sqrt {1+(\omega CR)^{2}}}}={\frac {1}{\sqrt {(\omega C)^{2}(({\frac {1}{\omega C}})^{2}+R^{2})}}}={\frac {({\frac {1}{\omega C}})}{\sqrt {\left(({\frac {1}{\omega C}})^{2}+R^{2}\right)}}}\\&={\frac {\vert X_{C}\vert }{\sqrt {X_{C}^{2}+R^{2}}}}\end{aligned}}}$

Instantaneous values

The time function for the sinusoidal oscillation is obtained from the imaginary part of the trigonometric form of the rotating complex vector:

${\displaystyle {\underline {H}}(t)={H}\cdot {e^{{\mathrm {j} }\cdot ({{\omega }{t}+{\varphi }})}}}$

${\displaystyle \operatorname {Im} ({\underline {H}}(t))={H}\cdot \sin({\omega }t+{\varphi })}$

For the time function it then follows:

${\displaystyle \ {H(t)}={\frac {1}{\sqrt {1+(\omega CR)^{2}}}}\cdot \sin {(\omega t+{\varphi })}}$

with the zero phase angle ${\displaystyle {\varphi }}$

Amplitude response

${\displaystyle H(\omega )={\frac {{\hat {u}}_{a}}{{\hat {u}}_{e}}}={\frac {1}{\sqrt {1+(\omega CR)^{2}}}}}$

Phase response

${\displaystyle \varphi (\omega )=-\arctan({\omega }{C}{R})}$

2nd order low pass

A second-order low-pass filter is obtained by connecting an inductance L in series with R , since its reactance X _L also has a frequency dependence - in the opposite direction to the capacitor reactance X _C. Here, R is chosen to be so large that there is little or no voltage increase in the frequency response.

Second order passive low pass

The transfer function of such a low pass is

${\displaystyle {\frac {{\underline {U}}_{a}}{{\underline {U}}_{e}}}={\underline {H}}(\omega )={\frac {\underline {Z_{2}}}{{\underline {Z}}_{1}+{\underline {Z}}_{2}}}}$

With

${\displaystyle {\underline {Z}}_{1}=R+\mathrm {j} X_{L},\quad {\underline {Z}}_{2}=-\mathrm {j} X_{C},\quad X_{L}=\omega \cdot L,\quad X_{C}={\frac {1}{\omega \cdot C}}}$.

Separated into real and imaginary parts:

${\displaystyle {\begin{aligned}{\underline {H}}(\omega )&={\frac {X_{C}}{X_{C}-X_{L}+\mathrm {j} R}}\\\\&={\frac {X_{C}^{2}-X_{C}\cdot X_{L}}{(X_{C}-X_{L})^{2}+R^{2}}}-\mathrm {j} {\frac {R\cdot X_{C}}{(X_{C}-X_{L})^{2}+R^{2}}}\end{aligned}}}$

The output voltage U _a thus drops faster above f _c (at R = 0 with 12 dB / octave or 40 dB / decade), since now not only | X _C | smaller, but at the same time | X _L | gets bigger.

For such LC low-pass filters, large inductances are required in the low-frequency range (up to several henries ). These have poor electrical properties and / or have very large geometric dimensions. A magnetic core is often used to reduce dimensions and losses. LC low-pass filters are used, for example, in power converters , in line filters , in crossovers for high frequency or in loudspeaker crossovers . In signal processing, such higher-order filters are implemented using operational amplifier circuits. These filters are then referred to as active low-pass filters (or active filters) and are also known as Sallen-Key filters after their inventors .

In applications where high efficiency is required, R will not be used to avoid heat loss. The voltage increase is then either desired, it is accepted or it is avoided by a finite load impedance of the filter. In transmitter systems , for example, the similar-looking pi filter is often used in order to attenuate harmonics , which are caused, for example, by the C operation of the transmitter tube , to a permissible level. The values ​​of the components can moreover be selected in such a way that the filter acts as a resonance transformer and produces a power matching between the transmitter output impedance on the one hand and the antenna cable or antenna on the other.

Higher order low pass

Frequency response measured with a network analyzer and Smith chart of a low-pass filter

By connecting several low-pass filters one after the other, you can increase their order. For example, two second-order low-pass filters connected in series form a fourth-order low-pass filter. The attenuation changes above the cutoff frequency by 4 · 20 dB / decade = 80 dB / decade, which corresponds to a slope of 24 dB / octave.

However, two interconnected low-pass filters with the same cut-off frequency do not result in a higher-order low-pass with the same cut- off frequency. Special formulas and tables are available for dimensioning a low pass with the desired cutoff frequency.

In addition, the problem arises that a low pass in a chain is influenced by the output resistance of the upstream and the input resistance of the downstream low pass. This effect can be counteracted with impedance converters .

In general, n storing elements (ie capacitors or coils) are required for an nth order filter.

The attenuation of a low-pass filter of the nth order increases above the cut-off frequency by n · 20 dB / decade.

Emphasis and Deemphasis

With static frequency response change, emphasis and deemphasis , the time constant is usually specified instead of the cutoff frequency .

See also

• High pass

literature

• Ulrich Tietze, Christoph Schenk and Eberhard Gamm: Semiconductor circuit technology. Springer-Verlag, 2002, 12th edition, ISBN 3-540-42849-6 .

Web links

• Use of capacitors in RC filters
• RC filter and cutoff frequency - low pass and high pass
• Video: low and high pass . Institute for Scientific Film (IWF) 2004, made available by the Technical Information Library (TIB), doi : 10.3203 / IWF / C-14821 .