Capacitor (electrical engineering)
A capacitor (from Latin condensare ' to compress' ) is a passive electrical component with the ability to statically store electrical charge and the associated energy in an electrical field in a direct current circuit . The stored charge per voltage is referred to as the electrical capacitance and is measured in the unit Farad . In an AC circuit, a capacitor acts as an AC resistor with a frequency-dependent impedance value .
In principle, capacitors consist of two electrically conductive surfaces, the electrodes , which are separated from one another by an insulating material, the dielectric . The size of the capacitance is determined by the area of the electrodes, the material of the dielectric and the distance between the electrodes. The electrodes and the dielectric can be rolled up or arranged in parallel as a stack. Industrially manufactured capacitors are supplied with capacitance values of around 1 picofarad (10 −12 F) up to around 1 farad , with supercapacitors even up to 10,000 farads.
By far the most widely produced capacitors are integrated storage capacitors in digital storage circuits . The most important types of capacitors are ceramic capacitors , plastic film capacitors , aluminum and tantalum electrolytic capacitors and, although they are based on completely different storage principles, the supercapacitors . In addition to these capacitors with fixed capacitance values, there are components with adjustable capacitance values, the variable capacitors .
Capacitors are used in many electrical systems and in almost all electrical and electronic devices . For example, you realize electrical energy storage as a DC link capacitors in frequency converters , as a storage capacitor in sample and hold circuits or as a photo-flash capacitors in flash units . They couple signals in crossovers of audio devices and, as highly stable class 1 capacitors, together with coils, form filters and resonant circuits . As smoothing capacitors in power supplies and backup capacitors in digital circuits , they can be found in the field of power supply. As interference suppression capacitors, they suppress electromagnetic interference signals and, as power capacitors, effect the desired phase compensation . Special designs of capacitors are used as sensors .
Unwanted capacitive interference from electrical fields of neighboring components in circuits and parasitic capacitances, so-called stray capacitances , do not belong to the capacitors. A series of actuators such as piezoelectric converters , electrostatic loudspeakers , baffles and components of electro-optics do not belong to the capacitors .
functionality
A capacitor blocks the direct current but forwards the alternating current .
Functioning in a DC circuit
After applying a direct voltage to a real capacitor with a series resistor , a monotonous electric current flows , which charges the electrodes with opposite polarity, so that a constantly increasing voltage is established in the capacitor. The electrical potential that builds up on the electrodes creates an electric field in the space between the electrodes , the field strength of which is proportional to the voltage built up.
In the case of a DC voltage source with constant internal resistance , the voltage across the capacitor follows an exponential function with a negative exponent, so that the current tends to zero asymptotically over time . If the voltage source and capacitor have the same voltage, no current flows (“the capacitor is charged”).
If the capacitor is disconnected from the voltage source, energy and charges are retained and the voltage remains constant. In general terms, this stores the charge on the electrodes by the capacitor. If energy is withdrawn from the capacitor by connecting a consumer, the field strength of the electric field decreases and with it the capacitor voltage.
Since the current flows through the entire circuit in a closed circuit, it also flows through the capacitor. Physically, however, the current in the circuit consists of two currents, a conducted current of charge carriers such as electrons or ions and a so-called displacement current in the space between the electrodes, which is to be understood as part of the effect of the electric field and with a corresponding change in the electric field strength goes hand in hand. In real capacitors, the space between the electrodes is filled with a dielectric . The displacement current then results, in addition to the portion due to the change in the field strength, from the charge displacement in the dielectric, the polarization , which results from its dielectric constant .
With low field strengths and linear dielectric materials, the polarization increases linearly with the voltage on the capacitor. The charge stored in the capacitor increases proportionally to the voltage. The constant of proportionality is called capacity; it is the essential feature of a capacitor. The greater the capacity , the more charge and energy a capacitor can store at a certain voltage . The equations
respectively
and
summarize that. is the charge (in coulombs , C, or ampere-seconds, As), the capacitance (in farads , F) and the voltage (in volts , V); the energy (in joules , J) is marked with to distinguish it from the field strength .
Real capacitors can only up to a maximum voltage, which results from the breakdown strength results of the dielectric, are loaded.
The time that a real capacitor needs to charge or to be discharged can be found in the article RC element .
Functionality in the AC circuit
Capacitors conduct alternating voltages and alternating currents in the AC circuit , but with a shift in the phase position between voltage and current, the current leads the voltage by 90 °. Because of their charge storage capacity, a current begins to flow in capacitors before the voltage changes, while in the case of a coil the voltage first changes before a current flows. Mnemonics:
- In the case of the capacitor: electricity leads.
- In the case of inductances: currents are delayed.
A capacitor with the capacitance (F) forms an alternating current resistance with the impedance (Ω) as a complex quantity in an alternating current circuit at the angular frequency as the quotient of the alternating voltage and the alternating current :
- .
The amount of the complex impedance is the impedance .
The impedance is smaller, the larger the capacity and the higher the frequency.
The property of capacitors as an alternating current resistance with the lowest possible impedance is used in many applications in addition to energy storage to separate direct and alternating current components, to correct phase shifts and to generate resonance circuits . The discharge differential equation, which is important for many applications, can be found in the article RC element .
history
Leiden bottle
The Leiden bottle is the oldest type of capacitor ( capacity around 5 nF). It consists of a glass vessel that is covered on the inside and outside with metal foil, usually made of aluminum. The glass acts as an insulator , later called "dielectric". The principle of the Leiden bottle was discovered independently in 1745 by the cathedral dean Ewald Jürgen Georg von Kleist in Cammin ( Pomerania ) and a year later by the physicist Pieter van Musschenbroek in Leiden , when they suffered electric shocks during laboratory tests with arrangements of glasses and metal parts .
The Leyden bottle and similar laboratory devices were mainly used for the public demonstration of electric shocks (also known as "Kleist's shock"), as knowledge about the nature of electricity increased later , as an energy source for more advanced experiments: Benjamin Franklin connected a Leyden bottle over a metal cord with a kite that he let fly into the sky. With this dangerous experiment he succeeded in transferring cargo from thunderclouds to the Leyden bottle. He coined the term " electrical condenser ".
Further development
An improved capacitor was invented in 1775 by Alessandro Volta (1745-1827), he called it " electrophorus " ( electrophorus , carrier of electricity). It consisted of two metal plates that were insulated from one another by a layer of ebonite . One can already consider this arrangement as a prototype of modern capacitors. The use of better dielectrics later led to a reduction in size. Around 1850, mica , a naturally occurring mineral, was sliced and used as an insulator; These capacitors were manufactured commercially from the time of the First World War . Wrapped paper capacitors with metal foil coatings have been in use since 1876.
Capacitors, which, through the chemical structure of an extremely thin dielectric made of non-conductive aluminum oxide on an aluminum anode and the use of a liquid electrolyte, led to capacitors with a higher capacity, the later " electrolytic capacitors ", were applied for a patent by Charles Pollak in 1896 Filter capacitor used to suppress humming noises in telephone networks.
Porcelain has also been used as a dielectric in capacitors since around 1900 . It was not until the 1930s that ceramic capacitors were developed as a result of research into further ceramic materials to replace porcelain and mica .
Mica as a dielectric in capacitors was first used in 1909 by William Dubilier in the USA and was the most widely used material for capacitors in communication devices until the outbreak of World War II. Nowadays, mica capacitors have been replaced by improved class 1 ceramic capacitors.
With the development of high-quality insulating plastic films from the field of organic chemistry after the Second World War , the industry began to replace the paper in metal-paper capacitors with thinner and more voltage-resistant plastic films, from which a wide range of different plastic film capacitors was developed.
From around 1950 General Electric in the USA began developing tantalum electrolytic capacitors . Here it was not only possible to achieve miniaturization through a considerably higher capacity per construction volume compared to the previously known capacitors, but with the development of a solid electrolyte, the long-term stability of electrolytic capacitors could also be significantly improved.
A further significant increase in capacity was achieved with the " low voltage electrolytic capacitor " patented by General Electric in 1957 , which was further developed by SOHIO and from 1971 by NEC to a market-ready component and initially received the name " double-layer capacitor ", from which now based on the findings the name supercapacitor became the pseudocapacitance .
Silicon capacitors are a more recent development. These result from the great experience of the semiconductor industry with structuring silicon and offer the user frequency-stable capacitance values up to the gigahertz range.
In the last few years there has been a development towards ever smaller construction volumes and towards surface-mountable (SMD) capacitors for all suitable capacitor types . In addition, especially in the case of aluminum and tantalum electrolytic capacitors, the introduction of new polymer electrolyte systems resulted in a considerable increase in the electrolyte conductivity and correspondingly lower loss resistance.

Current (2009) research deals, among other things, with new surface structuring of the electrodes. For example, with a nanostructure in the form of billions of small holes lying next to each other in a thin aluminum layer, coated with titanium nitride / aluminum oxide / titanium nitride as a capacitive structure, the power density of a nanocapacitor , measured in W / kg, can be increased by more than ten times compared to electrolytic capacitors and thus achieves a storage capacity in the order of magnitude of double-layer capacitors , without having their disadvantage of the limited charging or discharging speed.
Another way to increase capacitance is to use better dielectrics. This is achieved, for example, by integrating barium titanate into a non-conductive matrix, which means that the permittivity is higher than that of ceramic capacitors, while the dielectric remains robust and malleable, as with film capacitors.
market
Capacitors can be found in almost all electrical and electronic devices. An industrial report estimated the value of all capacitors sold worldwide in 2008 to be US $ 18 billion. Ceramic capacitors accounted for US $ 8.3 billion (46%), aluminum electrolytic capacitors US $ 3.9 billion (22%), plastic film and metal paper capacitors US $ 2.6 billion (15%), tantalum electrolytic capacitors 2.2 US $ billion (12%), double-layer and supercapacitors US $ 0.3 billion (2%) and other capacitors such as vacuum capacitors US $ 0.7 billion (3%). In particular, the development in the field of new telecommunication devices and tablet computers with their MLCC chip capacitors has significantly advanced the market. Of the approximately 1.4 trillion (1.4 · 10 12 ) capacitors (2008), MLCC chips alone accounted for about 1 trillion (1.0 · 10 12 ).
The market for industrially manufactured capacitors required by industry fell somewhat in the years that followed, because more expensive capacitors were often replaced by cheaper solutions. For example, tantalum chips have been replaced by MLCCs. The capacitor market was estimated at $ 16.9 billion in 2016.
Calculation of the capacity
For a number of idealized electrode arrangements, the field distribution in the capacitor and thus its capacity can be precisely determined. The following table shows some important arrangements:
| designation | capacity | Electric field | Schematic representation |
|---|---|---|---|
| Plate capacitor | |||
| Cylinder capacitor | |||
| Spherical capacitor | |||
| Bullet |
It means: the electrode area, its distance, its length and its radii , the electric field constant of the vacuum, the relative permittivity of the dielectric and the electric charge .
In the schematic representation, the electrodes are colored light gray or dark gray and the dielectric is colored blue. It should be noted here that in the case of the plate capacitor and cylinder capacitor arrangements, only the capacitance portion is calculated by this dielectric shown in blue. Since there are also fields outside of the dielectric shown - which, figuratively speaking, bulge out laterally - the given formulas are only approximations, which become better the smaller the distance between the electrodes compared to their length.
In a modified version, plate capacitors allow very high capacitances per volume: By alternately stacking the electrodes connected to a potential on top of one another, they become doubly effective. The illustration of the multilayer capacitor makes this clear. If the plates are designed as a metal foil or film, they can also be wound up with a suitable insulator, which also doubles the effect. Due to its compact design, this is the most common capacitor.
Cylinder capacitors are mostly only used in special applications, for example as vacuum or bushing capacitors. The equation given for the design is also helpful in determining the capacitance per unit length of a coaxial line .
In the case of spherical capacitors, the special case, of importance, is the capacity of a free-standing sphere. Here the counter-electrode is formed by the environment, so it is usually at ground potential . The capacity of this design is very low. For example, a sphere with a radius of 15 cm, as used in the Van de Graaff generator to store charge or in Tesla coils to form an LC resonant circuit , theoretically has a capacity of approx. 16.7 pF. In practice, however, the capacity is higher because the counter electrode (earth) is not infinitely far away. In the CGS system of units, the capacitance of a spherical capacitor is equal to the radius of the sphere in centimeters, so the above-mentioned sphere has a capacitance of 15 cm (cm is the unit of capacitance in this system). Since the electric field is very homogeneous on the spherical surface, large spherical capacitors can be charged to several million volts before a spark discharge occurs.
Applications
Energy and charge storage
A typical application in power electronics is intermediate circuit capacitors in switched-mode power supplies and converters . Here a circuit (for example rectifier , four-quadrant controller ) takes over the rectification of alternating current , this circuit part acts as a power source. A second part of the circuit acts as a sink (for example an inverter ). The intermediate circuit capacitor has the task of absorbing the pulsating current from the rectifier and supplying the inverter with a sufficiently constant voltage. The larger its capacity, the smaller the voltage change due to the current draw between the charging pulses. The smoothing capacitors at the output of DC voltage converters and in DC voltage power supplies also have the same function ; they keep their ripple voltage as low as possible.
In a similar way, capacitors can provide high power for a limited period of time (see also double-layer capacitor ). They are charged to a certain voltage and can then drive consumers with high, short-term power requirements. Examples of this are the high-voltage capacitor ignition in internal combustion engines and the “ exploding-bridgewire detonator ” in weapons technology .
A typical application is found in flash units . A capacitor is charged from a battery to around 400 V within a few seconds using a voltage converter . After the flash tube has been ignited, the capacitor discharges within a few microseconds and delivers a power of several kilowatts. The battery itself can not possibly provide that much power due to its high internal resistance .
The same applies to the defibrillators used in medicine today . Implantable defibrillators work with voltages of around 650 to 800 V and a shock energy of 30 J with a battery voltage of around 3.5 V. The capacities of the capacitors are around 100 to 170 μF.
Back-up capacitors are used to stabilize the supply voltage in high-frequency and complex digital circuits. Here, for each integrated circuit or circuit section, one or more capacitors are connected in parallel to the supply voltage, which act as a voltage or energy source in moments of high current or power demand. Due to their low impedance at high frequencies, they reduce the impedance of the higher-level power supply or its supply line and prevent the power supply of subcircuits from influencing each other. Conversely, capacitors can absorb disruptive, temporary overvoltages in electronic circuits and thus prevent their spread and harmful effects. This is called smoothing or blocking and those components are called smoothing or blocking capacitors. If the overvoltages are caused by switching operations on relays or power semiconductors , the capacitors are specifically referred to as quenching or snubber capacitors .
Furthermore, interconnections of several capacitors are used to raise, lower and invert supply voltages. Here capacitors are cyclically charged to one potential, connected to another potential and discharged there. Common circuits are the charge pump and its special design as a high-voltage cascade .
For applications in which the fastest availability is not important, other storage technologies are more economical for storing larger amounts of energy .
Frequency-dependent resistance
For use as a frequency-dependent reactance , the capacitor must have a known capacitance, since the capacitance value has a direct influence on the capacitive reactance. In the following, applications of the frequency-dependent reactance are mentioned as they occur in electrical power engineering , communications engineering , analog and digital technology .
Blocking capacitors
Low-induction (ceramic) capacitors are necessary in all electronic circuits in order to reduce the dynamic internal resistance of the power supply to such an extent that even very high-frequency current pulses of, for example, 2 GHz do not cause any inadmissible voltage fluctuations on the inductive resistance of the lead wire . Therefore these capacitors have to be connected directly to the IC.
Energy Technology
In AC power engineering, special power capacitors are used for reactive power compensation to change the phase position between current and voltage: If many inductive loads (such as electric motors, fluorescent tube chokes and transformers) are operated in medium-sized and large industrial and plant facilities, this happens because of them Total inductance to a (sometimes considerable) inductive reactive current . If there is no compensation, this would increase the energy bill and require larger cross-sections of the supply lines within the energy distribution of the plant to the power plant. Rather, the inductive phase shift (corresponding to the total inductance of the currently active consumers) is automatically compensated for within the plant power distribution by connecting or disconnecting suitable capacitors. In the case of smaller electric motors, reactive current compensation is usually carried out directly on the motor using a capacitor. For effective reactive current compensation, the compensation capacitors and the motor and transformer inductances must always have the same antiphase impedance if possible . H. the power factor is kept at a value close to 1 at the power transfer point of the power plant in the plant's energy distribution center.
The capacitor is also used in a capacitor motor, in which it shifts the phase position of the alternating current together with a field coil of the motor, which ultimately generates a rotating magnetic field . Through an external phase shift capacitor, z. For example, a three-phase motor (L1, L2, L3) can be operated with a loss of active power while observing the operating voltage on the single-phase power supply (L, N or L, L) ( Steinmetz circuit ).
To reduce voltages or as a capacitive series resistor instead of a heat loss (active) resistor or a comparatively expensive transformer, the capacitor is used in a capacitor power supply: There it works on a large alternating voltage (usually the mains voltage ) and supplies a small alternating current , the z. B. at a Zener diode together with a normal reverse current diode generates a tapped voltage, which can then be used as a supply voltage in a subsequent circuit. However, there is no galvanic separation between the mains and consumer circuit.
Filter applications
The frequency dependence of the alternating current resistance is used to increase or decrease alternating voltages depending on the frequency, to " filter " them. A simple circuit is the RC element , which, depending on the circuit, acts as a high or low pass. The coupling capacitor, which is used to separate direct currents from superimposed, higher-frequency alternating current components, represents a borderline case of the high-pass filter. This is necessary, among other things, to the operating point at Analog - amplifiers to hold adjustable.
Together with coils , which have a certain inductance as a characteristic , ohmic resistors and possibly active components, capacitors are also used in electronic circuits for resonant circuits , band filters and crossovers . This results in a certain resonance frequency. Corresponding circuits are also high-pass or low-pass, but can be produced with a higher quality . An example of this are the crossovers in loudspeakers .
A time-discrete variant of special filters that use capacitors in their structure are the switched capacitor filters . Furthermore, coils can be simulated in filters using so-called gyrators : The capacitance of a capacitor is converted into the inductance of a coil using an active circuit replicated.
Converter
The voltage that builds up on a capacitor is proportional to the integral of the charging current over time. In this way, capacitors are used to define switching times, for example a capacitor determines the switching times of an astable multivibrator . To do this, a capacitor is charged via a power source ; its voltage increases in proportion to the elapsed time. As soon as the voltage exceeds a certain value, the state of the circuit changes. A number of converter circuits are implemented in a similar manner:
- Voltage-frequency converter: This circuit converts an input voltage into a frequency proportional to it. A capacitor is cyclically charged by a voltage-controlled constant current source up to a specified voltage, then suddenly discharged. The frequency of the sawtooth-shaped voltage curve on the capacitor is the output signal.
- Analog-digital converter based on the slope principle: this converter is similar to the voltage-frequency converter, but does not necessarily work cyclically.
- Time measurement: Here the current source is controlled by a pulse of unknown length, the voltage of the capacitor after the end of the pulse is proportional to the pulse length.
- Frequency-voltage converter: For frequency measurement, pulses of constant length are generated in time with the frequency to be measured. These periodically charge a capacitor from which a constant discharge current is drawn. The voltage across the capacitor is the output signal.
See also: NE555 , an integrated circuit for timer or oscillator circuits developed in 1971.
Information store
The state of charge of a capacitor can represent information in digital or analog form. Analog information storage by means of a capacitor takes place, for example, in the sample-and-hold circuit : during the sampling phase, a capacitor is connected to an input signal voltage from which it is separated during the holding phase. The voltage value is then constantly available for further processing, typically an analog-to-digital conversion (ADC). Another type of analog information storage is the bucket chain storage .
Several billion capacitors can be combined in an integrated circuit to store large amounts of information . Examples include dynamic RAM (DRAM), eraseable programmable read only memory (EPROM), and flash memory .
Capacitors as sensors and actuators
Special designs of capacitors are suitable as sensors for a number of physical quantities . These variables cause a change in the capacitance or the contained charge, both of which can be evaluated by a subsequent circuit. Non-linear capacitors are known in particular configurations. A capacitance standard is a capacitor with the highest absolute and relative constant capacitance against temperature changes and aging. In addition, the highest demands are usually placed on the electrical quality over a large frequency range and on the dielectric absorption of the dielectric used of less than a few microvolts. Also thermoelectric voltages are unwanted here. These calibration capacitance standards are used to calibrate (adjust) high-quality measuring devices such as B. Precision RLC measuring bridges are used or are in these devices.
The measuring principles can be divided into the following two groups:
Change of electrode geometry
The capacitance of a capacitor changes with the distance between the electrodes. For example, capacitors can be used for distance and thickness measurement by mechanically coupling an electrode with the measured variable and the change in the measured variable is transferred to a change in the plate distance. For example, the thickness of the lacquer layer or the distance between a nozzle during laser material processing can be determined. This group also includes the capacitive proximity switch and the capacitive touchscreen . With the latter, the distance to the finger is evaluated spatially resolved.
Also, acceleration can be detected in this way: Due to the inertia of a movable electrode, for example, in a micromechanical acceleration sensor , an acceleration varies the distance between the electrodes of a capacitor. Pressure sensors ( manometers ) are constructed in a similar way - a change in pressure causes a change in the distance between the plates. The condenser microphone also works according to this principle, converting the sound pressure or sound pressure gradient into an electrical signal.
Among other things, the electrostatic loudspeaker uses the electrostatic attraction of the electrodes. The compressive force on the spaced plane-parallel plates of a capacitor at voltage is
with - permittivity
The pressure is thus dependent on the square of the field strength and can be greatly increased by using puncture-proof materials , see also dielectric elastomers .
Alternatively, a measured variable can also change the coverage of the electrodes, which also changes the capacitance. For example, angles can be measured by rotating electrodes in the form of a segment of a circle against one another, similar to the rotary capacitor described below .
Change of dielectric
With a capacitive hygrometer , the humidity influences the dielectric constant of a special insulation material and in this way the capacitance.
The capacitive level sensor is also based on a change in the dielectric constant . Here the electrodes are attached in such a way that they immerse further into the liquid as the level increases. Due to the higher permittivity of the liquid, the capacity increases with increasing diving depth.
Types and forms
| Pedigree of capacitors for use in electronic devices | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the course of the history of capacitors, many industrially used types, also called families or technologies, have developed. According to the grouping in the international and national standards, these are divided into capacitors with fixed capacitance, the "fixed capacitors", and capacitors with variable capacitance, the "changeable or variable capacitors ".
Fixed capacitance capacitors, fixed capacitors
Fixed capacitors have a defined capacitance value that is provided with a tolerance. There are depending on the technical requirements such. B. dielectric strength, current carrying capacity, capacity stability, temperature coefficient, frequency range, temperature range or type of mounting (SMD version) as well as economic requirements (price) in numerous different technology families, versions or designs.
The most important industrially manufactured fixed capacitors are ceramic , plastic foil , aluminum and tantalum electrolytic capacitors and supercapacitors , formerly called "double-layer capacitors". Ceramic and plastic film capacitors have capacitance values in the range from a few picofarads to around 100 microfarads. Electrolytic capacitors start at around 1 microfarad and extend into the farad range. In addition, supercapacitors have capacitance values in the kilofarad range.
Ceramic capacitors
Ceramic capacitors have ceramic dielectrics with dielectric strengths of 10 to 100,000 V with different levels of permittivity . They form a large group of capacitors in the lower capacitance range (0.5 pF to 100 µF or more). The types of ceramics used belong on the one hand to the paraelectric materials with field strength-independent relative permittivity, for example titanium dioxide (TiO 2 ), on the other hand to the ferroelectric materials with field strength-dependent relative permittivity, such as for example barium titanate (BaTiO 3 ). Ceramic capacitors are made from finely ground granules by sintering in a temperature range between 1200 and 1400 ° C. By means of suitable additives ( aluminum - silicates , magnesium silicates, aluminum), the relative permittivity ε r of a ceramic capacitor 6-14000 lie. Ceramic capacitors are divided into two classes based on their ceramic type and related electrical properties: Class 1 capacitors, which are suitable for high frequency and filter applications, and Class 2 capacitors, which are used as energy storage and filter capacitors.
Plastic film capacitors
Plastic film capacitors use films made of plastic or plastic mixtures as the dielectric and are produced in two versions:
- Plastic film capacitors with metal coverings each consist of two plastic films, both of which are covered with a metal film, usually made of aluminum, and are rolled up together to form a roll. With the usual smaller designs, the metal foils protrude alternately in opposite directions beyond the plastic foil, so that one of the metal foils protrudes on each side of the roll, which is then contacted over a large area and with low induction with the respective connection.
- In the simplest case, metallized plastic film capacitors consist of two plastic films, each of which is coated with aluminum on one side. These are wound up with a slight offset to the side so that the metallized foils protrude from the winding on opposite sides and can therefore be contacted. This design is also available as layer capacitors - the layers are layered to form a large block from which the individual capacitors are sawn out. Metallized plastic film capacitors, like MP capacitors, are self-healing in the event of a breakdown , since the thin metal layer of the coverings evaporates from the voltage breakdown arc around the breakdown channel.
Metal paper capacitors
Metal paper capacitors (MP capacitors) consist of two aluminum-metallized paper strips ( insulating paper ), which are rolled up with another paper film to form a roll and installed in a cup. The winding is impregnated with an insulating oil, which increases the dielectric strength and reduces the loss factor. MP capacitors are mainly used as power capacitors in the field of power electronics and for network applications as interference suppression capacitors . They are self-healing due to the metallized coverings, like comparable plastic film capacitors.
Electrolytic capacitors
Electrolytic capacitors (also called electrolytic capacitors) are polarized capacitors with an anode electrode made of a metal ( aluminum , tantalum and niobium ) on which an extremely thin, electrically insulating layer of the oxide of the anode metal is generated through electrolysis ( anodic oxidation , formation ) , which forms the dielectric of the capacitor. To enlarge the surface, the anode is structured, in the case of aluminum electrolytic capacitors the anode foil is roughened, in the case of tantalum and niobium electrolytic capacitors, metal powder is sintered to form a sponge-like body. The electrolyte can consist of a liquid electrolyte ( ion conductor ) or a solid electrolyte ( electron conductor ) and forms the cathode of the electrolytic capacitor, which has to adapt perfectly to the structured surface of the anode. Power is supplied to the electrolyte via foils of the same metal as that of the anode or via another suitable contact. With the exception of bipolar electrolytic capacitors, electrolytic capacitors are always polarized components; the anode is the positive connection. They must never be operated with incorrectly polarized voltage (risk of explosion) and can be destroyed even with a slight overvoltage. For better protection against polarity reversal, there are designs with three pins, which are arranged in the form of an irregular triangle and can therefore only be soldered into the circuit board in a certain position. The third pin is either unconnected, connected to the housing or to the cathode, depending on the manufacturer. By connecting two anode foils in series with opposite polarity in a capacitor housing, bipolar electrolytic capacitors for alternating voltage operation are also produced for special applications (e.g. audio frequency crossovers). The latest developments in the field of electrolytic capacitors are aluminum and tantalum electrolytic capacitors with polymer electrolytes made of conductive polymers, which are characterized by particularly low internal ohmic losses.
Super capacitors
| Family of super capacitors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Supercapacitors , formerly called " double layer capacitors ", ( English electrochemical double layer capacitor , EDLC ) have the highest energy density of all capacitors. Their high capacity , based on the building volume, is based on the one hand on the physical phenomenon of extremely thin electrically insulating Helmholtz double layers on the surfaces of special large-area electrode materials , in which the electrical energy is storedstatically as double-layer capacitance in electrical fields . On the other hand, a further part of the high capacity very often comes from a so-called pseudocapacity , a voltage-dependent electrochemical or Faraday storage of electrical energywithin narrow limits, which is associated with a redox reaction and a charge exchange at the electrodes, although in contrast to accumulators No chemical change occurs on the electrodes. Using special electrodes, the pseudocapacitance can achieve a considerably higher value than the double-layer capacitance with the same structural volume.
The respective share of the double-layer capacitance and the pseudocapacitance in the total capacitance of the capacitor can be seen in a very rough generalization through the naming of such capacitors in industrial publications.
- Double layer capacitors
- store the electrical energy mainly in the Helmholtz double layers of their electrodes and have no or only a small proportion of pseudocapacitance in the total capacity (up to about 10%)
- Pseudocapacitors
- Due to their electrode construction with high redox capacitance, they usually have a significantly higher proportion of the pseudocapacitance, which means that they have a higher specific capacitance than double-layer capacitors.
- Hybrid capacitors
- are supercapacitors with a static double-layer electrode and an electrochemical redox electrode, whereby the redox electrode can be similar from a different technology, for example from the field of accumulators or electrolytic capacitors .
In all supercapacitors, the electrolyte forms the conductive connection between two electrodes. This distinguishes them from electrolytic capacitors , in which the electrolyte forms the cathode , i.e. the electrolyte is an electrode that is connected to the negative terminal of the capacitor. Like electrolytic capacitors, supercapacitors are polarized components that can only be operated with the correct polarity .
Supercapacitors are sold under many different trade names such as B. BestCap, BoostCap, DLCAP, EVerCAP, DynaCap, Faradcap, GreenCap, Goldcap, SuperCap, PAS, PowerStor or Ultracapacitor as well as the lithium-ion capacitors under Premlis, EneCapTen, Ultimo or LIC.
Other types
- Vacuum capacitors
- They are advantageous for large high-frequency currents and voltages in the kilovolt range and are preferably used in high-power transmitters . There are also designs with variable capacities.
- Glass dielectric
- allows a wide temperature range from -75 to +200 ° C; typical values are 300 pF to 100 nF.
- Capacitors on a silicon substrate
- In integrated circuits, capacitors are conventionally manufactured using a sequence of layers of silicon , silicon oxide , and aluminum . Silicon and aluminum form the electrodes of the capacitor; the silicon oxide (also silicon nitride ) forms the dielectric. If a particularly large number of capacitors is required, as in semiconductor memories , dielectrics with a higher dielectric constant that are more difficult to process are also used. In special cases, if the storage contents are to be preserved without an energy supply, also ferroelectrics .
A similar process is also used to manufacture discrete capacitors that have good properties at frequencies up into the gigahertz range.
- Mica capacitors
- have a dielectric made from the naturally occurring mineral mica . This has a high dielectric strength and, due to its layer structure, can be split into thin flakes down to 20 µm thick, which are usually vapor-deposited with silver as electrode coatings. Mica capacitors are used due to the low loss factors in transmission technology and due to their high capacitance constancy and low capacitance tolerance in measurement standards and in filter and oscillating circuit applications for high requirements. They are often referred to as mica capacitors, after the English word for mica.
In addition to the division of capacitors according to the dielectric used or, in the case of electrolytic capacitors, according to the cathode, they can also be classified according to the area of application or design. Important examples are:
- Power capacitors
- are metal paper or plastic film capacitors. They can be operated directly on the supply network voltage and are characterized by a larger design, depending on the power range with plug-in or screw connections and usually through earthable sheet metal housings and are functionally intended for a high current-carrying capacity.
- Feed-through capacitors
- are mostly coaxially constructed capacitors, often ceramic capacitors, which lead an electrical line through a conductive wall (shield). The internal connection protrudes from the capacitor on both sides at the ends of a conductive coating and forms the bushing for an electrical connection. The external electrode of the capacitor is contacted with the wall. The capacitance, which acts between the inside and outside connection, diverts high-frequency interference, for example radio waves from the environment, from a device feed line to ground .
- Guard ring capacitors
- are a special design of a plate capacitor to reduce edge effects in measurement processes.
Fixed capacitor designs
The designs of fixed capacitors used industrially today reflect the development of industrial technology over the past 100 years. The designs at the beginning of the 20th century were still mechanically fastened with screws and the connections were soldered or screwed on by hand. The price pressure in manufacturing led to circuit board technology in the middle of the 20th century . For this, wired components were required and the capacitors were developed with connecting wires accordingly. In order to save costs with more compact circuit boards, the initially horizontal designs with axial connections were later transformed into radial, upright designs. These are often offered with the same electrical values, with different spacing between the connections, the pitch (RM).
In the course of miniaturization and standardization, driven by the development of ever more extensive circuits, the triumphant advance of surface-mountable components, the so-called SMD chips , began in the 1980s . They enable more compact circuit boards with higher manufacturing quality and lower process costs.
In addition to the components for the industrial mass business, there are also designs that result from the special requirements of the respective circuit. For example, the ribbon connections of film capacitors for high pulse current carrying capacity, the screw connections of large aluminum electrolytic capacitors for high current carrying capacity or special designs for, for example, feed-through capacitors.
Also integrated circuits contain a large number of capacitors. Depending on the requirements, these can exist between different layers of the IC with an insulator (= dielectric ) in between . The capacitor plates can, for. B. consist of different metal or polysilicon layers. In the case of DRAMs in particular , each memory cell usually consists of a capacitor with an associated transistor . See also MIS capacitor .
Variable capacitors
Variable capacitors are electrical capacitors, the capacity of which can be adjusted continuously and reproducibly within defined limits manually or with a regulated motor control. They are mainly in filters and oscillators for tuning of transmitters or receivers , and for impedance matching used, being replaced by the possibility of adjustability other necessary individual capacitors of many individual circuits with different frequency.
There are mechanical and electrical variable capacitors.
The mechanically variable capacitors belong to the passive components and are divided into variable capacitors , which are designed for transmitter tuning for frequent and repetitive actuation, and trimming capacitors (trimmers), which are designed for one-off or infrequent actuations for fine tuning.
Most of the designs of the mechanically variable capacitors are only of historical significance, including the clear, air-dielectric rotating capacitors that were typical for tuning older radios. These mechanical capacitors have been replaced by capacitance diodes or VCO- controlled PLL circuits since the 1970s .
Nowadays (2017) still required mechanical designs are u. A.
- Variable vacuum capacitors for devices with higher power such as B. in MRI scanners.
- Multiturn tubular trimmers , which can be set very precisely due to the effective rotation angle of the spindle, which is a multiple of 360 degrees (multiturn) and are suitable for microwave applications in radar devices as well as in medical and industrial devices up to 100 GHz.
- SMD trimmers with the smallest dimensions in circles with very low power for e.g. B. mobile phones, remote-controlled access systems, surveillance cameras, DVD devices and burglar alarms., As well as
- Laser adjustment capacitors , the top electrode of which can be vaporized step by step with the help of a precisely controllable laser beam. A desired capacitance value can thus be set with a very high degree of accuracy.
An adjustable capacitance value can for circles with smaller performances by electrically-variable capacitors , and varactors called ( varactor ) be accomplished. These capacitors are active components and use the properties of semiconductor technology to obtain a variable capacitance. Electrically variable capacitors include
- Capacitance diodes ( varicap diode ) in which electrically influenced by change of the space charge region can be varied, the electrode spacing and hence the capacitance.
- Dielectric variable capacitors ( dielectric varactors ), for example integrated variable BST capacitors or BST varactors ( BST varactors ), the specialty of which is the dielectric made from the ferroelectric material barium strontium titanate (BST) . BST has a relatively high relative permittivity , which is dependent on the field strength in the dielectric. This means that the capacity of the BST varactors depends on the applied voltage.,
- Digital variable capacitors ( Digitally Tunable Capacitors (DTC) ) are arrangements of a plurality of integrated capacitors in integrated circuits of different semiconductor technologies that can be / serially connected in parallel across digitally coded switch so that achieved a desired capacitance value for tuning a resonant circuit or Filters is needed. and
- Electrically variable RF MEMS capacitors ( Tunable RF MEMS capacitors ), in which the force is used with which oppositely charged movable electrodes in micro-electromechanical systems attracteach otherwhen a voltage is applied in order to generate electrically adjustable capacitance values.
The parameters of these electrically variable capacitors are strongly influenced by special properties of semiconductor technology. I.a. the small dimensions lead to significantly smaller realizable capacitance values, which however makes these capacitors suitable for higher frequencies up to a few 100 GHz. You will u. a. Used in filters for frequency selection in modern stationary and mobile receivers.
Markings
There is no such uniform marking for capacitors as there is for resistors . Some common variations are listed below. More information can be found using the web links below .
Identification of the capacity
- 473 : The first two digits indicate the value in picofarads, the third the number of subsequent zeros. 473 means 47 × 10 3 pF = 47000 pF = 47 nF.
- 18 : Often found on ceramic wired capacitors as an imprint, means a specification in picofarads, here 18 pF.
- 3n9 : Means 3.9 nF.
- .33 K 250 : The first number gives the value in microfarads, i.e. 0.33 µF = 330 nF. K stands for a capacitance tolerance of 10% and 250 for the nominal voltage in volts for which the capacitor is designed and which may be applied continuously in the entire specified temperature range (J, K and M stand for ± 5%, ± 10% and ±, respectively 20%).
- For the increasingly rare axial design, color codes were also common.
In the middle of the 20th century, paper capacitors in particular, which were used in the first tube receivers for radio reception that were emerging at that time , were often labeled with the unit “cm”, the unit of capacitance in the electrostatic CGS unit system , which is hardly used today .
The illustration on the left shows a paper capacitor made by SATOR from 1950 with a capacity of “5,000 cm” at a test voltage of “2,000 V”. That would be a capacitance of around 5.6 nF in today's common SI system of units . A capacity of 1 cm in the CGS system of units corresponds to 1.1 pF in the SI system of units, the conversion factor is 4 π ε 0 .
Other markings
- Also when it is electrolytic capacitors , an encoded in several digits date code printed on, to be able to detect the date of manufacture, since electrolytic capacitors as a function of time can reduce its capacity; For example 2313: 2 = 2002, 3 = March, 13 = 13th day, i.e. 13th March 2002. The structure of the codes can differ from one manufacturer to the next, as only a few are based on uniform standards. (See also marking of electrolytic capacitors )
- If the design of the capacitor allows it, the manufacturer, the operating temperature range, the dielectric strength and a series designation are attached that provide information about the insulator used.
- Ceramic capacitors are marked with their tolerance and the valid temperature range.
- The designations X1 , X2 , X3 and Y1 to Y4 are used to identify interference suppression capacitors for use in line filters in the low-voltage network . X capacitors are used between the outer conductor and the neutral conductor . The X1 type withstands a voltage pulse of 4 kV, X2 of 2.5 kV. Thanks to a special construction, they do not catch fire even if they are overloaded. The Y types are used when protective insulation is bridged and its defect can lead to an electric shock; they withstand voltage pulses twice as high.
Circuit symbols
In the circuit symbols shown below, the horizontal surfaces symbolize the separated electrodes. In Europe, electrical symbols are standardized in EN 60617 Graphical symbols for circuit diagrams or IEC 60617 . In North America, the standards ANSI / IEEE Std 91a – 1991 IEEE Graphic Symbols for Logic Functions , IEEE Std 315–1986 (Reaffirmed 1993) / ANSI Y32.2–1975 (Reaffirmed 1989) / CSA Z99–1975 Graphic Symbols for Electrical and Electronics Diagrams used.
Standardization and equivalent circuit diagram
Discrete capacitors are industrial products, approximately 1400 billion (1.4 · 10 12 ) units of which were manufactured and installed in 2008. For capacitors, the electrical values and the criteria of their measurement methods are harmonized in the international area by the framework specification IEC 60384-1, which was published in Germany as DIN EN 60384-1 (VDE 0565-1) in May 2010. This standard initially defines the electrical values of a capacitor with the help of a series equivalent circuit diagram. In it are:
- C is the capacitance of the capacitor,
- R isol , the insulation resistance of the dielectric or R Leak , the resistance that represents the residual current in electrolytic capacitors,
- ESR ( Equivalent Series Resistance ), the equivalent series resistance, which summarizes the ohmic line and dielectric polarity reversal losses of the capacitor
- ESL ( Equivalent Series Inductivity L ), the equivalent series inductance, it summarizes the parasitic inductance of the component.
With this equivalent circuit diagram, the regulations in DIN EN 60384-1 and the respective subordinate design specifications, the operating states of capacitors can be described in such a way that reproducible measurement results can be achieved for defined boundary conditions (frequency, temperature, applied voltage).
Electrotechnical and system theoretical description
A series of descriptions has been developed for the different areas of application, which emphasize certain aspects of the behavior of a capacitor.
Field energy
A charged capacitor stores electrical energy in the electrical field that exists between the charged plates. If a capacitor of capacitance is charged to the voltage , its field contains the energy according to:
To charge a capacitor, electrical charges are transported from one plate to the other. The more the capacitor is charged during this process, the stronger the electric field already prevailing between its plates , the more force is exerted to move the charge from one plate to the other. As the voltage of the capacitor increases, more and more work is therefore done for a further increase in voltage. In the end, the total work done during charging is stored as field energy. When unloading this becomes free again.
Loading and unloading process
For a charging or discharging process, the relationships apply
and
- .
It is
- the Euler's number
- the capacitor voltage at the time
- the charging current at the time
- the source voltage applied to the capacitor
- the capacitor voltage at the time
- the difference between capacitor voltage and source voltage
- the time constant of the capacitor
- the internal resistance of the capacitor, or the sum of internal and series resistance in an RC element
- the capacitance of the capacitor
Charging process
During the charging process of a capacitor via an RC element , the voltage and current curve (over time) can be described by the following e - functions :
- and
with as the instantaneous value of the voltage across the capacitor, as the instantaneous value of the current across the capacitor, as the ohmic (pre-) resistance of the capacitor (in the circuit ), as a time constant and as the charging voltage. After a charging time of, a capacitor reaches a voltage of ; after a charging time of only around 50%, a capacitor has already reached 50% of its final or original voltage. It is charged to around 99% after a charging time .
Unloading process
The course of the electrical voltage and the electrical current (in time) during the discharge process of a capacitor can be represented as functions as follows:
- such as
with as the voltage of the charged capacitor. After a discharge time of only a voltage of (= 1 / e) is applied to a capacitor ; after a discharge time of approximately the voltage has dropped to half. After a discharge time of , the voltage has dropped to around 1% ( residual currents / leakage currents must be observed).
Time range
A relationship between current and voltage results from the time derivative of the element equation of the capacitor :
This means that the current through the capacitor is proportional to the change in voltage across the capacitor. The statement that the current is proportional to the time derivative of the voltage can be reversed: The voltage is proportional to the time integral of the current. For example, if a constant current is applied, a constant voltage change follows, the voltage increases linearly.
The charging and discharging of a capacitor by a voltage source via a resistor results in an exponentially flattening voltage curve. It is covered in detail in the article RC element .
Phase shift and reactance
A cosine-shaped alternating voltage with the amplitude and the frequency or the angular frequency , i.e.
on a capacitor causes the current to flow
- .
The current flows staggered in time to the voltage (" phase shift "), it leads it by or 90 °.
The current is proportional to the frequency of the applied voltage and the capacitance of the capacitor:
The ratio of voltage amplitude to current amplitude is generally referred to as impedance ; in the case of an ideal capacitor, in which the current leads the voltage by exactly 90 °, as a capacitive reactance :
Phase shift angle:
Reactance:
The formula shows that the electrical reactance of the capacitor decreases with increasing frequency up to a practical short circuit at high frequency and, on the other hand , becomes infinitely large at frequency , i.e. with direct voltage , and practically acts like a line interruption.
Due to the phase shift of 90 ° between voltage and current, no power is converted into heat at a reactance on average over time ; the power only oscillates back and forth and is referred to as reactive power .
If periodic non-sinusoidal alternating currents flow through a capacitor, these can be represented by means of Fourier analysis as a sum of sinusoidal alternating currents. For this, the combination of voltage and current on the capacitor can be applied separately to each individual sinusoidal oscillation , the resulting non-sinusoidal voltage curve on the capacitor then results as the sum of the individual sinusoidal voltage curves.
This composition only applies if the capacitance of the capacitor does not depend on the voltage applied. In this case, the capacitor is a linear component and the circuits built up with it are accessible using the methods of complex AC calculations. Does the capacitance of the capacitor depend on the instantaneous values of the applied voltage, i. That is, the dielectric conductivity of the dielectric located between the plates depends on the electric field strength if a non-linear capacitor is present. In this general case, the above relationships between current and voltage across the capacitor cannot be applied.
Example for the compensation of a phase shift
The parallel connection of a resistor and a capacitor, shown opposite, is connected to the 230 V power supply; the specified currents flow at 50 Hz. 2.3 A active current flows through the resistor, which must be paid for, the electricity meter must not react to the reactive current of 1.45 A and the connection cable must be rated for the total current of 2.72 A (the current through the capacitor is less than 90 ° out of phase so the total current is :) . An active power of 529 W is offset by a reactive power of 334 var (W), which oscillates between the generator and capacitor and unnecessarily loads cables and transformers.
To compensate for this reactive power, a suitably selected inductance of 0.5 H is connected in parallel to the device, the reactive current of which is also 1.45 A. The reactive currents of the capacitor and coil compensate each other due to their opposite phase positions and the total current consumption drops to 2.3 A. The entire arrangement now resembles a damped oscillating circuit .
Impedance
In particular, systems with several capacitors, resistors and coils are cumbersome to describe using the above formalism. In order not to have to calculate the phase and magnitude of signals separately, in the complex AC calculation the amplitudes of sinusoidal and cosinusoidal voltage curves are combined into imaginary and real components of a complex amplitude of the circular function extended to the complex level , with the imaginary unit and the circular frequency . Small letters for voltages and currents indicate variables that change over time; Quantities that are constant over time are marked with capital letters; complex sizes are underlined:
The real part of this gives the instantaneous value of the size.
The relationship between current and voltage, the impedance , can be obtained from this analogous to the ohmic resistance by forming quotients:
As an example, the amount of the impedance of a 5 nF capacitor at 3 kHz is calculated:
You can see that the effective resistance for the (ideal) capacitor is equal to 0 and the reactance is automatically given the negative sign.
This approach avoids differential equations. Instead of the derivative there is a multiplication with (mathematically negative direction of rotation).
Since real capacitors not only have a capacitance but also still have parasitic effects (series equivalent resistance ESR , Equivalent Series Resistance , series equivalent inductance ESL , Equivalent Series Inductance L ), the phase shift between current and voltage changes. It is no longer 90 °, but takes on a value that is smaller by the loss angle . With a phasor diagram , not only the impedance but also the phase shift angle and the additional loss angle can be shown in a clear way . It should be noted that this diagram only applies to one frequency.
If the series replacement values of a capacitor are known, then the impedance can also be calculated using these values. It is then the sum of the geometric (complex) addition of the effective and reactive resistances, i.e. the equivalent series resistance ESR and the inductive reactance minus the capacitive reactance . The two reactive resistances have the following relationships with the angular frequency :
The impedance is accordingly the amount of the geometric (complex) addition of the real and reactive resistances:
(For the sign convention used, see note under reactance , for derivation see under Complex AC Calculation ).
In the data sheets of the manufacturers of capacitors, the amount of the impedance, i.e. the impedance, is usually given.
Loss factor, quality and series resistance
Real capacitors have parasitic losses that result from the resistance of the supply lines and the dielectric losses. They have the effect that the phase shift between current and voltage at the terminals of a real capacitor is no longer exactly 90 °, but is reduced by the so-called loss angle . This angle is called tangent words and then called loss factor (ger .: dissipation factor , abbreviated DF ). It results from the tangent of the phase angle between the geometric sum of the reactances and and the equivalent series resistance ESR . Neglecting the inductance ESL , the loss factor , the ESR and the capacitance of a capacitor at a certain frequency are linked with the following formula:
For small values of (expressed in radians ) the following applies:
In the case of low-loss class 1 ceramic capacitors, instead of the loss factor, its reciprocal value, the quality or the quality factor is often specified.
This value relates to the bandwidth at the resonance frequency and is calculated according to the equation:
- ,
where the bandwidth (defined as the frequency range at the limits of which the voltage level has changed by 3 dB compared to the mean value)
results (with as upper and lower limit frequency). Since the shape of the impedance curve in the resonance range is steeper the smaller the ESR, a statement about the losses can also be made with the specification of the quality or the quality factor.
The definition of the specification of the losses in a capacitor described above is based on the generally accepted series equivalent circuit diagram specified in the basic specification DIN EN (IEC) 60384-1, in which the dielectric and line losses are combined to form the ESR or loss factor. To explain the loss factor, however, some specialist books use a different equivalent circuit diagram in which the ohmic losses are modeled by a resistor Rp, which (in addition to the insulation resistance) is connected in parallel to an ideal capacitor with the capacitance . (Then, when the ohmic losses are equated with the dielectric losses in these descriptions, then takes the from the knowledge out that the line losses are negligible in these capacitors.) The power loss thus results in the operation of the capacitor to an AC voltage with the RMS to
The reciprocal of this resistance is the conductance and is also known as the derivative . The tangent of the loss angle can be in the form
being represented.
Spectral range
A description in the image area of the Laplace transform avoids the restriction to harmonic oscillations. The following then applies to the impedance in the image area
It is the "complex frequency", characterizes the exponential envelope, turn the angular frequency.
Parallel connection
Capacitors are connected in an electrical circuit as a parallel circuit if the same voltage is applied to all components. In this case, the capacities of the individual components add up to the total capacity:
The parallel connection increases both the total capacity and the current-carrying capacity of the circuit. The total current flow I tot is distributed over the k th capacitor according to:
In addition to increasing the capacitance and current-carrying capacity of the circuit, capacitors connected in parallel also reduce their undesired parasitic properties such as inductance (ESL) and equivalent series resistance (ESR).
Series connection
A series connection occurs when the same electrical current flows through two or more capacitors. Then the reciprocal of the capacity of the individual components is added to the reciprocal of the total capacity:
The series connection is used, for example, to distribute a high voltage to several capacitors with a lower dielectric strength when no individual component is available for this voltage. Since the insulation resistances or, in the case of electrolytic capacitors, the residual currents of the individual capacitors can be very different, different insulation resistances or residual currents can result in a voltage distribution that does not match the capacitive voltage distribution. As a result, individual capacitors may be subjected to excessively high voltage, which could lead to short circuits. For this reason, capacitors connected in series are usually balanced, that is, a defined high-ohmic resistance (but significantly lower than ) is connected in parallel with each capacitor so that a defined voltage distribution is created.
I²t value for charging and discharging processes
When charging and discharging capacitors, the value is important for dimensioning the short-term load on semiconductors ( limit load integral ) and fuses (melting integral). For the components through which the charging or discharging current flows, the time-dependent value is calculated as follows:
or
with as charging or discharging time, as initial capacitor voltage when discharging or as charging voltage when charging, as capacitor capacitance, as charging or discharging resistance, as initial current and as time constant. The following applies to full charging and discharging :
or
Material and design-related features
Capacity and dielectric strength
The vast majority of industrially manufactured capacitors are designed as plate capacitors in the broadest sense. The capacity is thus obtained from the surface of the electrodes , the dielectric constant of the used dielectric and the reciprocal value of the distance of the electrodes to each other. In addition to these three parameters, which can differ considerably in real capacitors, the processability of the materials plays a decisive role. Thin, mechanically flexible foils can be easily processed, wrapped or stacked, to form large designs with high capacitance values. In contrast, wafer-thin, metallized ceramic layers sintered to form SMD designs offer the best conditions for miniaturizing circuits.
| Capacitor family | dielectric | Dielectric constant at 1 kHz |
Maximum dielectric strength in V / µm |
Minimum thickness of the dielectric in µm |
|---|---|---|---|---|
| Ceramic capacitor , class 1 | paraelectric | 20 ... 40 | <100 (?) | 0.5 |
| Ceramic capacitor, class 2 | ferroelectric | 200 ... 14000 | <25 (?) | 0.5 |
| Plastic film capacitor | PET | 3.3 | 580 | 0.7 |
| Plastic film capacitor | PEN | 3.0 | 500 | 0.9 |
| Plastic film capacitor | PPS | 3.0 | 470 | 1.2 |
| Plastic film capacitor | PP | 2.2 | 650 | 1.9 |
| Aluminum electrolytic capacitor | Al 2 O 3 | 8.4 ... 9.6 | 710 | 0.01 |
| Tantalum electrolytic capacitor | Ta 2 O 5 | 24 ... 28 | 625 | 0.01 |
Real capacitors cannot be charged to any voltage . If the permissible voltage, which is determined by the dielectric strength of the respective dielectric, is exceeded up to the " breakdown voltage ", the capacitor breaks down, which means that a considerably larger current suddenly flows through a spark gap or in a similar way. This usually leads to the destruction of the capacitor (for example a short circuit or even an explosion), and often to further destruction of the devices. The maximum dielectric strength of a capacitor depends on the internal construction, the temperature, the electrical load from charging and discharging currents, and in AC voltage applications also on the frequency of the applied voltage and on aging.
In the case of ceramic capacitors, it is not possible to determine a physically based, precise breakdown voltage of a ceramic layer for a defined thickness. The breakdown voltage can vary by a factor of 10, depending on the composition of the electrode material and the sintering conditions. Even with plastic film capacitors, the dielectric strength of the film varies greatly depending on influencing factors such as the layer thickness of the electrodes and electrical loads.
Metallized plastic film capacitors have the ability to heal themselves; a breakdown only leads to local evaporation of the thin electrodes. However, the capacitor loses a certain, small part of its capacitance without its functionality being impaired.
Electrolytic capacitors are polarized components. The dielectric strength of the oxide layers only applies if the voltage is correctly polarized. Reverse polarity voltage destroys the electrolytic capacitor.
Frequency dependence
The frequency dependence of the capacitance and the loss factor of capacitors results from two components:
- from the frequency-dependent behavior of the dielectric of capacitors. This influences the capacitance value, which decreases with increasing frequency, and the losses in the dielectric, which usually increase with increasing frequency. For details see Dielectric Spectroscopy .
- a design-related, parasitic inductance (connections, structure), which is shown in the equivalent circuit as a series inductance. It is called ESL ( equivalent series inductance L ) and leads to a characteristic natural resonance frequency at which the capacitor has its minimum impedance.
If an application requires a low impedance over a wide frequency range, capacitors of different types are connected in parallel. It is known to connect an electrolytic capacitor in parallel with a ceramic capacitor or to connect ceramic capacitors of different sizes in parallel.
Temperature dependence
The capacitance of a capacitor depends on the temperature, with the different dielectrics causing great differences in behavior. For ceramic capacitors there are paraelectric dielectrics with positive, negative and near zero temperature coefficients. Some plastic film capacitors also have similar properties. In the case of high stability requirements for oscillating circuits , for example , temperature influences from other components can be compensated for. Ceramic capacitors made of ferroelectric ceramics and electrolytic capacitors favorably have a very high permittivity, which leads to a high capacitance value, but also have a high, mostly non-linear temperature coefficient and are therefore suitable for applications without great demands on stability such as screening, interference suppression, coupling or Decoupling.
| Capacitor family, dielectric material | designation | ΔC / C | Usual temperature range |
|---|---|---|---|
| Ceramic capacitor class 1, paraelectric | NP0 / C0G | ± 0.3% or ± 30 ppm / K | −55 ... + 125 ° C |
| Ceramic capacitor class 2, ferroelectric | X7R | ± 15% | −55 ... + 125 ° C |
| Ceramic capacitor class 2, ferroelectric | Y5V | +22% / −82% | −30 ... + 85 ° C |
| Film capacitor, polyphenylene sulfide (PPS) | (F) KI, MKI | ± 1.5% | −40 ... + 150 ° C |
| Film capacitor, polypropylene (PP) | (F) KP, MKP | ± 2.5% | −40 ... + 105 ° C |
| Film capacitor, polyethylene naphthalate (PEN) | (F) KN, MKN | ± 5% | −40 ... + 150 ° C |
| Film capacitor, polyester (PET) | (F) KT, MKT | + 5% | −40 ... + 125/150 ° C |
| metallized paper (oil-soaked) | MP | ± 10% | −25 ... + 85 ° C |
| Aluminum electrolytic capacitor, Al 2 O 3 | ± 20% | −40 ... + 85/105/125 ° C | |
| Tantalum electrolytic capacitor, Ta 2 O 5 | ± 20% | −40 ... + 125 ° C |
Voltage dependence
Ferroelectric class 2 ceramic capacitors show a voltage-dependent, non-linear course of the capacitance. This results in a distortion factor in audio applications, for example . Film capacitors are therefore often used there where high quality requirements are concerned.
Formally, a non-linear capacitor can be described by a relative permittivity that depends on the instantaneous voltage . This relative permittivity is therefore not constant, but is to be viewed as a function of the voltage across the capacitor . For example, for a non-linear capacitor, the voltage-dependent capacitance is given as:
The function depends on the material.
Depending on the type of ceramic, class 2 ceramic capacitors show a drop in capacitance of up to 90% compared to the standardized measuring voltage of 0.5 or 1 V at nominal voltage.
Aging
The electrical properties of some capacitor families are subject to aging processes; they are time-dependent.
Ceramic class 2 capacitors with dielectrics made of ferroelectric materials exhibit a ferroelectric Curie temperature . Above about 120 ° C, the Curie temperature of barium titanate , the ceramic is no longer ferroelectric. Since this temperature is clearly exceeded when soldering SMD capacitors, the dielectric areas of parallel dielectric dipoles are only formed again when the material cools down. However, due to the lack of stability of the domains, these areas disintegrate over time, the dielectric constant decreases and thus the capacitance of the capacitor decreases and the capacitor ages. Aging follows a logarithmic law. This defines the aging constant as the decrease in capacity in percent during a decade of time, for example in the time from 1 hour to 10 hours.
Aluminum electrolytic capacitors with liquid electrolytes age due to the slow, temperature-dependent drying of the electrolyte over time. At first the conductivity of the electrolyte changes, the ohmic losses (ESR) of the capacitor increase. Later on, the degree of wetting of the porous anode structures also decreases, as a result of which the capacity decreases. If no other chemical processes occur in the capacitor, the aging of "electrolytic capacitors" can be described using the so-called "10-degree law". The service life of these capacitors is halved if the temperature acting on the capacitor increases by 10 ° C.
Also, double-layer capacitors are subjected to aging by evaporation of the electrolyte. The associated increase in ESR limits the possible number of charging cycles of the capacitor.
Impedance and resonance
The areas of application of capacitors predominantly use the property as a capacitive alternating current resistor for filtering , sieving , coupling and decoupling of desired or undesired frequencies or for generating frequencies in resonant circuits . For this reason, the frequency behavior of the impedance is a decisive factor for use in a circuit function .
The amount of impedance, the apparent resistance , is often shown in data sheets for capacitors as a curve over frequency . As the frequency rises, the impedance initially decreases to a minimum in the curve, from which it rises again. This curve is the result of the construction of real capacitors, which not only have a capacitance but also a parasitic inductance (ESL) in series . (See paragraph “Standardization and equivalent circuit diagram”). Capacitance and inductance ESL form a series resonant circuit, which at the frequency
gets in resonance. At this point the impedance only has a real component, the ESR of the capacitor. At higher frequencies the inductive component predominates; the capacitor is therefore ineffective as such, since it now acts like a coil .
Due to their large capacitance, conventional aluminum electrolytic capacitors have relatively good screening properties in the range of low frequencies up to about 1 MHz. However, due to their wound structure, they have a relatively high inductance , so that they are unsuitable for use at higher frequencies. Ceramic and film capacitors are suitable for higher frequencies up to a few 100 MHz due to their smaller capacities. They also have significantly lower parasitic inductance values due to their design (front contact of the foils, parallel connection of the electrodes). In order to be able to cover a very wide frequency range, an electrolytic capacitor is often connected in parallel with a ceramic or foil capacitor.
Many new developments in capacitors aim, among other things, to reduce the parasitic inductance ESL in order to be able to increase the switching speed of digital circuits, for example, by increasing the resonance frequency. Much has already been achieved here thanks to the miniaturization, especially of SMD multilayer ceramic chip capacitors ( MLCC ). A further reduction in the parasitic inductance has been achieved by contacting the electrodes on the long side instead of the transverse side. The face-down construction, combined with the multi-anode technology, has also led to a reduction in the ESL of tantalum electrolytic capacitors. But new capacitor families, such as MOS or silicon capacitors, also offer solutions when capacitors are required for very high frequencies up into the GHz range.
Ohmic losses
Ohmic losses in discrete, commercially available capacitors for electronics arise due to dielectric repolarization losses in the alternating field and due to the ohmic resistance of the leads and the electrodes of the capacitor. In the case of aluminum electrolytic capacitors , the limited conductivity of liquid electrolytes in particular contributes to these losses. The various loss resistances are combined to form a common value because they cannot be measured separately for industrially manufactured capacitors. They can be shown in the respective data sheets as a loss factor , as a quality and as an equivalent series resistance ESR. The numerical value of the loss factor and the quality is, with the same measuring frequency, within a specified range independent of the capacitance value of the capacitor. The ESR, on the other hand, is independent of the reactances and is a variable that characterizes each capacitor individually. About him can with the help of the equation
it is easy to calculate the heat loss that occurs in the condenser when there is a current load .
For power capacitors such as B. vacuum capacitors , large ceramic and polypropylene film capacitors, the ohmic losses are defined differently. Instead of loss factor, quality or ESR, the maximum current or pulse load is often specified here. This information is also ultimately an expression of the ohmic losses of the capacitor and is determined from the permissible heat loss that arises from the ohmic losses during the current load.
The ohmic losses of capacitors depend on the design and are therefore specific to a certain production technology. Within a design, the ohmic losses decrease with increasing capacity. At first glance, this seems paradoxical, because the higher the capacity, the greater the dielectric losses. That this is not the case is due to the technical structure of the capacitors. This is illustrated by the example of the ceramic multilayer capacitors. The many individual capacitors in the layer composite are connected in parallel, so that their individual loss resistances are also connected in parallel. This reduces the total resistance according to the number of individual capacitors connected in parallel. In the case of film capacitors , the end face contact of the winding has a similar effect. The type of contact can be described as a large number of individual capacitors connected in parallel. In the case of electrolytic capacitors , in which the lead losses through the electrolyte largely determine the ohmic losses, the increasing number of lead paths can be understood as a parallel connection of many individual resistors with increasing electrode areas, which reduces the total ohmic losses. In the case of very large aluminum electrolytic capacitors, multiple contacting of the anode and cathode foils often reduces the ohmic losses. For the same reason, tantalum electrolytic capacitors are manufactured with multiple anodes in some embodiments.
The ohmic losses are alternating current losses, direct current losses (insulation resistance, residual current) are mostly negligible with capacitors. The AC frequency for measuring the losses must be clearly defined. However, since commercially available capacitors with capacitance values from pF (picofarad, 10 −12 F) to several 1000 F for supercapacitors with 15 powers of ten cover an extraordinarily large capacitance range, it is not possible to cover the entire range with just one measuring frequency. According to the basic specification for capacitors, DIN EN (IEC) 60384-1, the ohmic losses should be measured with the same frequency that is also used to measure the capacitance, with:
- 100 (120) Hz for electrolytic capacitors and other capacitors with C > 10 µF
- 1 kHz (reference frequency) or 10 kHz for other capacitors with 1 nF ≤ C ≤ 10 µF
- 100 kHz, 1 MHz (reference frequency) or 10 MHz for other capacitors with C ≤ 1 nF
The ohmic losses of capacitors are frequency, temperature and sometimes also time dependent (aging). A conversion of the unit tan δ into ESR and vice versa is possible, but requires some experience. It can only take place if the measurement frequency is far enough away from the resonance frequency. Because at the resonance the capacitor changes from a capacitive to an inductive component, the loss angle changes dramatically and is therefore no longer suitable for conversion.
Ohmic losses of different class 1 capacitor types
The quality and the loss factor are characteristic quantities of the ohmic losses in the dielectric of certain capacitors, in which the line losses are negligible. These capacitors, called "Class 1" for ceramic capacitors, are mainly used in frequency-determining circuits or in high-performance applications as power capacitors. Large manufacturers usually use 1 MHz as the measuring frequency for the capacitance range of 30 pF to 1 nF that is common in electronics. This high frequency also refers to the use of such capacitors, which are predominantly in the higher frequency range. The affected small capacitance values with the associated low ESL values also ensure that the measured value is still far enough away from the resonance frequency.
The following table, in which the ESR values were calculated, gives an overview of the ohmic losses (maximum values) of different capacitor types (without power capacitors) at 1 MHz in frequency-determining applications in electronics:
| Capacitor type | Capacity in pF |
ESR at 100 kHz in mΩ |
ESR at 1 MHz in mΩ |
tan δ at 1 MHz in 10 −4 |
Quality Q |
|---|---|---|---|---|---|
| Silicon capacitor | 560 | 400 | - | 2.5 | 4000 |
| Mica capacitor | 1000 | 650 | 65 | 4th | 2500 |
| Class 1 Ceramic Capacitor (NP0) | 1000 | 1600 | 160 | 10 | 1000 |
Ohmic losses of different types of capacitors in the medium capacitance range
The capacitance range from 1 nF to 10 µF is mainly covered by class 1 and class 2 ceramic capacitors and by plastic film capacitors. Electrolytic capacitors are used less frequently in this capacity range. This capacity range is characterized by a large number of different applications with very different requirements. The ohmic losses of these capacitors are mainly specified in the manufacturers' data sheets using the loss factor. However, alternating voltage and pulse capacitors are also located in this area, which are specified via a current load.
As a general example, the following table lists the loss factors (maximum values) at 1 kHz, 10 kHz and 100 kHz and the ESR values derived from them for a 100 nF capacitance value.
| Capacitor type | ESR at 1 kHz in mΩ |
ESR at 10 kHz in mΩ |
ESR at 100 kHz in mΩ |
tan δ at 1 kHz in 10 −3 |
tan δ at 10 kHz in 10 −3 |
tan δ at 100 kHz in 10 −3 |
|---|---|---|---|---|---|---|
| Class 1 Ceramic Capacitor (NP0, N750) |
1600 | 160 | 16 | 1 | 1 | 1 |
| Class 2 Ceramic Capacitor (X7R, Y5V) |
4000 | 400 | 40 | 2.5 | 2.5 | 2.5 |
| PP film capacitor (polypropylene) |
6400 | 800 | 160 | 4th | 5 | 10 |
| PET film capacitor (polyester) |
12700 | 2400 | 480 | 8th | 15th | 30th |
| PEN film capacitor (polyethylene naphthalate) |
12700 | 2400 | 480 | 8th | 15th | 30th |
| PPS film capacitor (polyphenylene sulfide) |
24000 | 3200 | 800 | 15th | 20th | 50 |
Ohmic losses of different capacitor types in the higher capacitance range
Capacitors with capacitance values greater than 10 µF are mainly used in applications in the field of power supplies, filter and backup circuits. It is the typical capacitance range in which electrolytic capacitors and high-capacitance multilayer ceramic capacitors are used. According to the basic specification for capacitors, DIN EN (IEC) 60384-1, the ohmic losses of such capacitors should be measured at 100 Hz (or 120 Hz). However, since the working frequencies in electronics have increased significantly in the last few decades and the switching power supply sector also operates with much higher frequencies, the data sheets, especially those of electrolytic capacitors, often contain the 100 kHz ESR values.
The following table gives an overview of the ohmic losses (maximum values) of various capacitor types for filter or support applications in the low-voltage range. The capacitance of around 100 µF and a dielectric strength of 10 to 16 V have been selected in order to compare the capacitor types with one another. Since the size of the unit plays a major role in this area of application in electronics, the dimensions are also listed in the table. The line with a capacity of 2200 µF is listed as an example of how low ESR values can be achieved with a larger capacity and size, even with the cheapest type of capacitor, the "electrolytic capacitor". Incidentally, the higher ESR with the "electrolytic capacitors" is sometimes even desirable in terms of circuitry, because the damping via these losses can prevent unwanted resonances on circuit boards.
| Capacitor type | Kap./Spg in µF / V |
L × W × H in mm³ or D × L in mm² |
ESR at 100 Hz in mΩ |
tan δ at 100 Hz in% |
ESR at 100 kHz in mΩ |
|---|---|---|---|---|---|
| Class 2 Ceramic Capacitor (X5R) | 100 / 6.3 | 3.2 x 1.6 x 1.6 | 2400 | 15th | typ. 2 |
| Class 2 Ceramic Capacitor (YV5) | 100 / 6.3 | 3.2 x 1.6 x 1.6 | 3180 | 20th | - |
| Tantalum electrolytic capacitor with polymer electrolytes |
100/10 | 7.3 x 4.3 x 2.8 | 1600 | 10 | 18th |
| Tantalum electrolytic capacitor with manganese dioxide electrolytes |
100/10 | 7.3 x 4.3 x 2.8 | 1275 | 8th | 150 |
| Aluminum electrolytic capacitor with polymer electrolytes |
100/10 | 7.3 x 4.3 x 1.6 | 960 | 6th | 15th |
| Aluminum electrolytic capacitor with liquid electrolyte |
150/10 | 6.3 x 5.8 | 2020 | 19th | 260 |
| Aluminum electrolytic capacitor with liquid electrolyte |
2200/10 | 12.5 × 20 | 130 | 18th | 90 |
AC load capacity

An alternating voltage or an alternating voltage superimposed on a direct voltage causes charging and discharging processes in a capacitor. An alternating current flows, which is colloquially also called ripple current . The effective value of this alternating current causes a power loss P V via the ohmic losses of the capacitor (ESR, loss factor) , which heats the component from the inside out.
or
The resulting heat is released into the environment via convection and heat conduction . The amount of heat that can be released into the environment depends on the dimensions of the capacitor and the conditions on the circuit board and the environment.
The permissible alternating current load of electrolytic capacitors and plastic film capacitors is generally calculated so that a maximum permissible internal temperature increase of 3 to 10 K occurs. For ceramic capacitors, the alternating current load can be specified in such a way that the heat generated in the capacitor does not exceed the specified maximum temperature at a given ambient temperature.
In the data sheets for film capacitors and ceramic capacitors, instead of an alternating current, a maximum permissible effective alternating voltage is often specified, which may be continuously applied to the capacitor within the nominal temperature range. Since the ohmic losses in the capacitor increase with increasing frequency, i.e. the internal heat development increases with constant effective voltage, the voltage must be reduced at higher frequencies in order to maintain the permissible temperature increase.
A high alternating current load is particularly critical with electrolytic capacitors . As the capacitor heats up, the expected service life is reduced. If the maximum permissible temperature is exceeded due to excessive alternating current load, the liquid electrolyte can under certain circumstances come into the boiling range and cause the capacitor to burst.
Insulation resistance and self-discharge
A real capacitor charged to a DC voltage will discharge itself over time. This effect can be described by a finite insulation resistance of the dielectric, which is connected in parallel to an ideal capacitor with the capacitance C. The current flowing is called the leakage current; in series it is often specified as a function of capacity. The temporal course of the falling capacitor voltage has the form
in which
is the self-discharge time constant . After this time , the capacitor voltage has dropped to 37% of the initial value. The self-discharge time constant is a measure of the insulation of the dielectric between the electrodes of a capacitor. This time constant is important, for example, when a capacitor is used as a time-determining element (for example in timing relays) or for storing a voltage value, such as in a sample-and-hold circuit or integrators .
According to applicable standards, ceramic capacitors of class 1 must have an insulation resistance of at least 10 GΩ, those of class 2 at least 4 GΩ or a self-discharge time constant of at least 100 s. The typical value is usually higher. Plastic film capacitors typically have an insulation resistance between 6 and 12 GΩ. For capacitors in the µF range, this corresponds to a self-discharge time constant of 2000 to 4000 s.
With electrolytic capacitors, the insulation resistance of the oxide layer dielectric is defined by the residual current of the capacitor.
The insulation resistance or the self-discharge time constant is in part strongly dependent on temperature and decreases with increasing temperature. The insulation resistance or the self-discharge time constant must not be confused with the insulation of the component from the environment.
Residual current, leakage current
In electrolytic capacitors the insulation resistance is not defined, but also "leakage" (Engl. The residual current, leakage current ) called.
The residual current of an electrolytic capacitor is the direct current that flows through the capacitor when a direct voltage is applied. It arises from a weakening of the oxide layer through chemical processes during storage times and through current bridges outside the capacitor cell. The residual current is dependent on capacity, voltage, time and temperature. It is also dependent on the previous history, for example the temperature load caused by a soldering process.
Due to the self-healing effects in electrolytic capacitors, the residual current usually decreases the longer the capacitor is connected to voltage. Although the magnitude of the residual current of modern electrolytic capacitors, when converted into an insulation resistance, is significantly smaller than that of film or ceramic capacitors, the self-discharge of charged electrolytic capacitors can take several weeks.
Dielectric absorption
Under dielectric absorption or dielectric relaxation refers to unwanted charge storage in the dielectric. As a result, a capacitor that has been charged for a long time and then discharged will slowly recharge after the discharge resistance or short circuit has been eliminated. Because voltages that can be easily measured arise after a few minutes, this effect is also known as the reloading effect . It must be taken into account with high-quality capacitors if they are to be used as capacitance standards, for example.
The cause of the effect is the non-ideal properties of the dielectric. Under the influence of an external electric field, elementary electrical dipoles are aligned in the direction of the prevailing field in some materials through atomic restructuring. This alignment takes place with a much slower time constant than the space charge process of the capacitor and consumes supplied energy. These polarizations do not immediately recede in the dielectric after the field effects are interrupted (switching off the operating voltage and complete discharge of the capacitor), so that a “residual voltage” on the capacitor layers remains detectable in the polarity of the voltage that was previously applied. This effect can be compared with the magnetic remanence (residual magnetism).
In practice, this often minimal electrical voltage rarely affects the electrical circuit. Exceptions are, for example, sample-and-hold circuits or integrators .
The size of the absorption is given in relation to the originally applied voltage and depends on the dielectric used.
| Capacitor type | Dielectric absorption |
|---|---|
| Air and vacuum capacitors, Teflon | not measurable |
| Plastic film capacitors, polypropylene dielectric | 0.01 to 0.05% |
| Plastic film capacitors, polyester dielectric | 0.2 to 0.25% |
| Ceramic Capacitors, X7R | 0.6 to 1% |
| Ceramic capacitors, Z5U | 2.0 to 2.5% |
| Aluminum electrolytic capacitors | about 10 to 15% |
The resulting voltage can be a hazard: it can damage semiconductors or cause sparks when short-circuiting connections. This effect is undesirable in measuring circuits, as it leads to incorrect measurement results. High-voltage and power capacitors, including larger aluminum electrolytic capacitors, are therefore transported or delivered short-circuited. This short-circuit bridge must be removed again after installation.
Litter or parasitic capacity
For physical reasons, every real electrical component has a more or less strong capacitive coupling with the environment (stray capacitance) or parallel to its desired behavior (parasitic capacitance). This capacitive behavior can have undesirable effects, especially at high frequencies.
Circuits that actually require a capacitor can sometimes be designed as a separate component without a capacitor because of this stray capacitance that is already present. In particular, capacitors in the picofarad range can be replaced by a corresponding formation of conductor tracks on a circuit board : Two opposing copper areas of 1 cm² have a capacitance of 0.2 mm, for example when using FR2 as the base material ( ε r = 3.4) 15 pF. The realization of such “capacitors” is, however, a question of price. A 15 pF MLCC class 2 ceramic capacitor, including the assembly costs and minus the circuit board area it requires, is significantly cheaper than 1 cm² circuit board area.
Unwanted capacitive coupling can also occur with a capacitor. In particular, wound capacitors are asymmetrical with respect to the outer surface. The “cold” part of the circuit (usually the ground), which carries the lower or lower-resistance alternating voltage potential, is connected to the outer layer in order to reduce the coupling of the capacitor to the environment. The situation is similar with trimming capacitors; this applies here to the connection that can be actuated for trimming in order to reduce its interference when actuated with a tool.
See also
literature
- Friedhelm Schiersching: Understanding and using capacitors . Kosmos, Stuttgart 1983, ISBN 3-440-05185-4
- Otto Zinke , Hans Seither: Resistors, capacitors, coils and their materials . Springer, Berlin 1982, ISBN 3-540-11334-7
- Peter Volkmann, Edgar P. Vorndran: Electric field and capacitor . VDE, Berlin 1999, ISBN 3-8007-2018-3 (= tasks electrical engineering + electronics . Volume 2)
- Wolfgang Just, Wolfgang Hofmann: Reactive Current Compensation in Practice: Execution, Energy Saving, Harmonics, Voltage Quality . VDE, Berlin 2003, ISBN 3-8007-2651-3
- Hermann Böger, Friedrich Kähler, Günter Weigt: Components of electronics and their basic circuits . Stam, Cologne 1996, ISBN 3-8237-0214-9 (= introduction to electronics , part 1)
- Heinz-Josef Bauckholt: Basics and components of electrical engineering . 7 edition. Hanser, Munich / Vienna 2013, ISBN 978-3-446-43246-8 , pp. 409ff
- DIN EN 60384-1
- Fritz Henze: reactive current and power factor . Fachbuchverlag, Leipzig 1955, DNB 451961005
- Stefan Hochsattel: " You will probably always need it ..." 75 years of capacitor production in Gera . Self-published by S. Hochsattel, Gera 2013, ISBN 978-3-00-043983-4
Web links
- Basics and functionality
- Things to know about the capacitor
- CapSite 2016 Introduction To Capacitors Technical details on industrially relevant capacitors
- Technical data and further information can be found on the manufacturer's website , in particular: AVX , Cornell Dubilier , epcos , ELECTRONICON , Europe Chemi-Con , KEMET , Nichicon , Panasonic, Capacitive Products , RUBYCON , VISHAY , WIMA
Individual evidence
- ↑ J. Ho, TR Jow, S. Boggs, Historical introduction to capacitor technology, Electrical Insulation Magazine, IEEE, January-February 2010 ieeexplore.ieee.org , ifre.re.kr
- ↑ Electric liquid condenser with aluminum electrodes, patent no. DRP 92564 on DEPATISnet
- ↑ J. Ho, TR Jow, St. Boggs: Historical Introduction to Capacitor Technology In: Electrical Insulation Magazine, 2010, 26, pp. 20-25 doi: 10.1109 / MEI.2010.5383924
- ↑ Patent US2800616 : Low voltage electrolytic capacitor. Published June 23, 1957 .
- ^ Parag Banerjee, Israel Perez, Laurent Henn-Lecordier, Sang Bok Lee, Gary W. Rubloff: Nanotubular metal-insulator-metal capacitor arrays for energy storage . In: Nature Nanotechnology . tape 4 , no. 5 , 2009, p. 292–296 , doi : 10.1038 / nnano.2009.37 .
- ↑ Katherine Bourzac: Tiny sandwiches for the big hunger for energy. In: Telepolis. April 20, 2009. Retrieved April 20, 2009 .
- ↑ Nano Center Improves Energy Storage Options . In: Nanotechnology Now , March 23, 2009, accessed August 11, 2009
- ↑ New Electrostatic Nanocapacitors Offer High Power and High Energy Density . In: Green Car Congress , March 17, 2009, accessed August 11, 2009
- ↑ super-kon.uni-halle.de
- ↑ highbeam business, Electronic Capacitors SIC 3675, Industry report business.highbeam.com ( Memento of the original dated February 12, 2010 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice.
- ^ J. Ho, TR Jow, S. Boggs, Historical Introduction to Capacitor Technology, PDF ifre.re.kr
- ↑ technavio, Global Passive Component Market, (24.24x0.6988 = 16.9) [1]
- ↑ LA Vsevolozhskii, VA Filinov: Methods of measuring nonlinear capacity . In: Measurement Techniques . tape 19 , no. 10 , 1976, p. 1497–1500 , doi : 10.1007 / BF01101215 .
- ↑ http://files.hanser.de/Files/Article/ARTK_LPR_9783446430389_0001.pdf Arnold Führer, Klaus Heidemann, Wolfgang Nerreter: Basic areas of electrical engineering Volume 2: Time-dependent processes , ISBN 978-3-446-43038-9 , page 62
- ↑ Technical documents from Jennings on vacuum capacitors
- ↑ Technical overview of variable and fixed vacuum capacitors from Meiden
- ↑ AVX, Ron Demcko, Performance Characteristics of Multilayer Glass Dielectric Capacitors Performance Characteristics of Multilayer Glass Dielectric Capacitors ( Memento of March 15, 2016 in the Internet Archive ) accessed on November 13, 2019
- ↑ ATC // AVX MOS Single Layer Capacitors, Metal Oxide Semiconductor PDF
- ↑ vishay.com Technical information on SiO 2 capacitors from Vishay
- ↑ Power capacitors from TDK EPCOS for different applications de.tdk.eu
- ↑ Power capacitors from ABB (English)
- ↑ Comet, Variable Capacitors, Product Overview
- ↑ Alfred Tronser, Microwave Tuning Elements, [2]
- ↑ Exxelia, Microwave tuning elements ( page no longer available , search in web archives: archive link )
- ↑ Murata, Trimmer Capacitors FAQ [3]
- ↑ Johanson, LASERtrim® tuning capacitors, [4]
- ^ Johanson, Trimming Characteristics of LASERtrim® Chip Capacitor [5]
- ↑ Gennum, Applications, Processing and Integration Options for High Dielectric Constant multi-layer thin-film barium strontium titanate (BST) Capacitors
- ^ ST's Parascan ™ Tunable Integrated Capacitors (STPTIC) Tunable Integrated Capacitors
- ↑ IT knowledge, DTC (digitally tunable capacitor)
- ↑ S. Lucyszyn, Review of radio frequency microelectromechanical systems technology, IEEE 2004, IEE Proceedings online no. 20040405 doi: 10.1049 / ip-smt: 20040405 Review of radio frequency microelectromechanical systems technology
- ^ Film Capacitors. General technical information . EPCOS, May 2009, accessed on August 11, 2009 (PDF; 1.8 MB)
- ↑ Conversion: 'bandwidth in octaves' N in quality factor Q and quality factor Q in 'bandwidth in octaves' N
- ↑ Wolf-Ewald Büttner: Fundamentals of Electrical Engineering 2 . Oldenbourg, 2004, ISBN 3-486-27296-9 , pp. 102 .
- ↑ Film Capacitors, TDK Epcos, General technical information (PDF; 1.4 MB)
- ↑ AVX, Dielectric Comparison Chart (PDF; 161 kB)
- ↑ Holystone, Capacitor Dielectric Comparison, Technical Note 3 (PDF; 64 kB)
- ↑ a b S. P. Murarka, Moshe Eizenberg, AK Sinha: interlayer dielectrics for semiconductor technologies . Academic Press, 2003, ISBN 0-12-511221-1 , pp. 338-339 .
- ↑ Metallized Polypropylene Film Energy Storage Capacitors For Low Pulse Duty, Ralph M. Kerrigan, NWL Capacitor Division ( PDF ( Memento of the original from September 29, 2013 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original - and archive link according to the instructions and then remove this note. )
- ↑ KW Plessner: Aging of the Dielectric Properties of Barium Titanate Ceramics . In: Proceedings of the Physical Society. Section B . tape 69 , 1956, pp. 1261-1268 , doi : 10.1088 / 0370-1301 / 69/12/309 .
- ↑ WIMA: inductance and natural resonance . ( Memento of February 28, 2007 in the Internet Archive ) Retrieved November 13, 2019
- ↑ Fundamentals of complex number calculation complexezahlen.com
- ↑ Silicon Capacitor, Vishay, HPC0603A
- ^ Simic Electronics, Chip Mica Capacitors
- ↑ AVX, C0G (NP0) class I ceramics avx.com
- ↑ Murata, C0G, 100 nF 50 V, 1206, Q> 1000/1 kHz, psearch.murata.com
- ↑ Holystone
- ↑ Wima, FKP3, 100 nF 63 V, MKS4, 100 nF 50 V, SMD-PEN, 100 nF 63 V, MKI2, 100 nF 63 V, wima.de ( Memento of the original from August 21, 2010 in the Internet Archive ) Info : The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Murata, X5R, 100 µF 6.3 V, 1206, Tan d 0.15 / 120Hz, Y5V, 100 µF 6.3 V, 1206, Tan d 0.2 / 100Hz, psearch.murata.com
- ↑ Kemet, Product Search, T491, T510, T520, T530, A700, 100/10 kemet.com
- ↑ Panasonic, SMD-FP, 150/10, panasonic.com
- ↑ Jianghai, CD 263 BK, 1000/10, 10x16 mm, xcnet.de (PDF)
- ↑ The Electronics Compendium: Capacitors
- ↑ WIMA: insulation resistance . ( Memento of the original from February 27, 2007 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.
- ↑ Modeling Dielectric Absorption in Capacitors , by Ken Kundert (in English; PDF; 352 kB)
- ↑ Table on dielectric absorption ( memento from March 20, 2013 in the Internet Archive ) accessed on November 5, 2019
- ↑ Danger from dielectric absorption (in English)
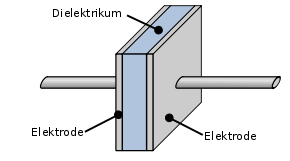
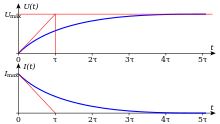


























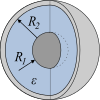











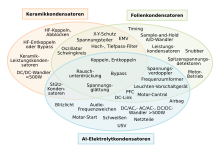








































































































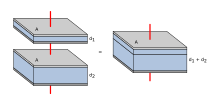



![[I ^ {2} t] _ {\ text {value}} (t) = {\ frac {{U_ {0}} ^ {2} C} {2R}} \ left (1-e ^ {\ frac {-2t} {RC}} \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccc5e3b4e8e6000121e0fd953ec8fcdb0744a32b)
![[I ^ {2} t] _ {\ text {value}} (t) = {\ frac {{I_ {0}} ^ {2} \ tau} {2}} \ left (1-e ^ {\ frac {-2t} {\ tau}} \ right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/178756f40e597d3d0356190671723ff2becc7d5d)




![[I ^ {2} t] _ {\ text {value}} = {\ frac {{U_ {0}} ^ {2} C} {2R}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2dcc57f9b279e61ba06a782615dafa4092fa3ea)
![[I ^ {2} t] _ {\ text {value}} = {\ frac {{I_ {0}} ^ {2} \ tau} {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ea1048e711f6b5953a26d4854c6cfc8f2290591)















