Coulomb's law
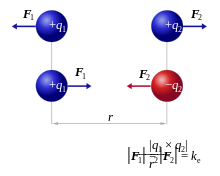
The Coulomb law or Coulomb's law is the basis of electrostatics . It describes the force acting between two point charges . It also applies to spherically symmetrically distributed electrical charges that are spatially separated.
The amount of this force is proportional to the product of the two amounts of charge and inversely proportional to the square of the distance between the centers of the spheres. Depending on the sign of the charges, the force has an attractive or repulsive effect in the direction of the straight line connecting the center points. In the attractive case, it behaves exactly like the force between two point masses according to the law of gravitation .
If there are more than two charges, the individual force vectors are added according to the superposition principle .
Coulomb's law is the basis of influence .
Coulomb force
Coulomb's law was discovered by Charles Augustin de Coulomb around 1785 and confirmed in extensive experiments. In the international system of units , in scalar form and in a vacuum, the force is accordingly
- ,
| , | spherically symmetrically distributed amounts of charge |
| Distance between the centers of the charge quantities | |
| electric field constant |
Vector shape
The vectorial notation of discrete charges gives the Coulomb force field to which a test charge is exposed in the field of a second charge , as follows:
Here are
- is the force on the test charge , caused by the charge ,
- and the position vectors of the two centers of charge and
is the unit vector pointing from (along the line connecting the two centers of charge) towards .
As can be seen, loads of the same name, i.e. H. repel those with the same sign, in accordance with the above definition, since the force in such a case has the same orientation as , while charges with unequal signs (unlike charges) attract, since the force then (analogous to Newton's law of gravitation ) has the opposite orientation of .
If the origin of coordinates is placed at the position of the load , the above equation simplifies to:
- .
Next is then
the vector of the field strength of the electric field generated by the central charge at the point , d. H. at a distance from the origin.
If the central charge that generates the field is replaced by a charge cloud with the charge distribution distributed in space, the integral replaces the formula given at the beginning for the Coulomb force on the test charge
- .
Coulomb's law in the form given at the beginning is included in this formula as a special case for a point charge distribution. Conversely, this more general form can also be derived from Coulomb's law using the superposition principle.
Coulomb's constant
The term appearing in the above equations
is also referred to as the Coulomb constant . Where is the speed of light . Since the magnetic field constant has almost exactly the value (until the new definition of the SI units in 2019, the value was exactly), it has almost exactly the numerical value of .
Form in the CGS system
In Gaussian units and in other CGS units , Coulomb's law is used to define the electrical charge. One charge unit acts on a second one at a distance of 1 cm with a force of 1 dyn. The basic electrical unit of the SI, CGS-ESU and CGS-EMU systems of units differs only in the definition of
- In the CGS-ESU is . Therefore the Coulomb constant has the value in this system of units .
- In the CGS-EMU is . Therefore, in this system of units, the Coulomb constant has the value .
Coulomb potential
As long as there is no temporal change in the magnetic field , the electric field is eddy-free and the energy difference when transferring a charge from A to B is therefore independent of the actual distance covered. Correspondingly, the electric field and the electric force can also be described by a potential .
In the case of the simple Coulomb force, the result is the Coulomb potential, which for a single point charge Q can be described as follows:
The constant of integration C is typically zero, so that the potential disappears at infinity. The potential difference between two points is the voltage drop U between these two points. The Coulomb potential is only valid exactly for static charges. In contrast, for moving point charges, in which magnetic fields also come into play, the Coulomb potential becomes a Liénard-Wiechert potential .
The potential electrical energy is also a potential, now with regard to the electrical force:
Here, too, it is customary to choose the boundary condition so that the potential energy at infinity becomes zero, i.e. is also zero here.
Coulomb force in a medium
Coulomb's law can easily be extended to the case of charges in homogeneous , isotropic , linear media. The material surrounding the charges must have these properties as a good approximation:
- It is electrically neutral.
- It fills the space between and around the charges evenly (homogeneously).
- The polarizability of the medium is independent of direction .
- The polarization is proportional to the electric field created by the charges.
In particular, the homogeneity requires that the atomic character of the matter is negligible compared to the distance between the charges.
For such media, Coulomb's law is written in the same form as in a vacuum, with the only difference that it is replaced by:
In isotropic media , the relative permittivity is a material constant that takes into account the polarizability of the medium. It can be obtained both through measurements and from theoretical considerations.
The reverse is true in a vacuum .
literature
- Dieter Meschede: Gerthsen Physics. 23rd edition, Springer, Berlin / Heidelberg / New York 2006, ISBN 3-540-25421-8 .