Influence
Influence ( Latin for influence ), also known as electrostatic induction , describes the spatial displacement of electrical charges through the action of an electrical field .
In a conductor , the mobile charges, almost always electrons, are shifted on the surface and change their place. This leads to location-dependent charge densities . The stuck atoms are not affected. The shift usually takes place until there is no longer any force acting on the freely movable load carrier, i.e. H. until the original electric field has been completely compensated by the electric field of the shifted charges and the space is field-free ( Faraday cage ). Charges cannot be shifted in or on a dielectric , but the atoms or molecules present are polarized .
Influence on electrical conductors
Electric charges of the same name (+ / + or - / -) repel each other, unlike (+/-) charges attract each other ( Coulomb's law ). If you bring a body with a conductive surface into an electric field, the charge density changes on it . This happens because negative and positive charges tend in other directions through the action of this field. On certain areas there are more charge carriers than on others. However, the total charge on the body remains constant.
The inside of a conductor, on the other hand, is always free of electrostatic fields, because the electrons can move in it until all differences are balanced.
Influence for charge separation in connection with changeable capacities is the basic functional principle in electrophoresis , influence machines , tape generators and also the signal voltage generation in electret microphones and electrostatic condenser microphones .
Electrically charged objects and charge carriers generate an electric field in their surroundings, which in the immediate vicinity due to its own shape, at a greater distance also depends on the fields and potentials of the environment. The electron carries the negative charge , the proton the positive charge. Charges of the same polarity repel each other. In conductive solids, electrons can easily be influenced by electric fields, while protons usually keep their position. In conductive gases or liquids, electrons can be influenced more easily by electric fields and are more mobile than protons because they have considerably less mass. That is why only electrons are often decisive for transporting electrical charges - the electrical current .
Number of electrons involved
By influence - measured in absolute numbers - very many electrons are shifted from their original places. Relative to the total of electrons present on the surface of a sphere, however, it is a very small fraction. An estimate should show that:
The breakdown field strength E critical in air is between 10 7 V / m for rough surfaces and 10 9 V / m for smooth surfaces. In the case of influenza tests, one must limit oneself to values below E max = 10 5 V / m, so that undesired discharges do not falsify the results. This allows the surface charge density σ to be estimated.
So every negatively charged square centimeter carries the excess charge 1.8 · 10 −10 As, which in turn corresponds to 1.1 · 10 9 electrons.
In order to estimate the number of unbound electrons present at all on this square centimeter, one has to know the number of atoms. A copper atom with an atomic radius of 200 · 10 −12 m occupies an area of 1.3 · 10 −19 m 2 . So about 8 · 10 14 atoms fill one square centimeter. Copper is an excellent electrical conductor, each atom represents approximately a conduction electron to the electron gas of the metal are available.
This leads to an estimate that the relative excess charge on a copper surface is approximately
amounts. For every 700,000 freely moving electrons of the metal that are "anyway" present, a single one is added when there is a strong negative electrical charge . In order to interpret the following images correctly, one has to imagine that each blue point represents around 100,000 unbound electrons.
example
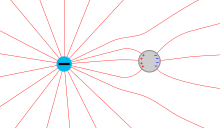
The picture above shows the symmetrical charge distribution on a spherical surface when other charged objects are very far away. Then every square millimeter of the surface contains the same number of positive and negative charges and the sphere appears uncharged. The charge density is zero on the entire surface because there is no excess charge anywhere. In the picture only the freely moving conduction electrons are drawn (with copper about one per atom) and only one proton per atom, although each copper core contains 29 protons. The effect of the remaining 28 protons is compensated for by the 28 electrons remaining in the atomic shell, which is why they are not shown.
The picture on the right shows where the freely moving electrons “flee” to when another negative charge is approached from the left. They would all prefer to run to the right side of the metal ball, because that is where the distance from the neighboring charge is maximal. The mutual repulsion prevents them from crowding into too narrow a space. In addition, there would then only be positive ions in the left hemisphere, which pull some electrons back to the left. Ultimately, within nanoseconds, there is a compromise between mutual aversion of the electrons, flight from the neighboring charge and attraction of the left hemisphere, which has become positive.
Every square millimeter of the right hemisphere contains more electrons than protons, so the charge density there is negative. These electrons are missing in the left hemisphere, so it is positive there. The charge density is balanced on a ring (with a horizontal axis) at right angles to the plane of the drawing, the center of which is roughly at the center of the sphere , where every surface element contains the same number of positive and negative charges. In the drawing, only the upper and lower parts can be drawn.
In the lower picture the “disturbing” neighboring charge has moved closer, as a result of which the freely moving electrons “flee” even further to the right. The charge density on the far right becomes even more negative, and on the far left even more positive than in the previous picture. The "neutral" ring also moves to the right. The field strength increases with the charge density and when a maximum value is exceeded, which depends on the radius of curvature and the surrounding gas, corona discharge sets in .
The accumulation of electrons on the far right must not be taken too literally. In reality the electrons are point-shaped and can therefore hardly take up space from one another. The electrons are drawn as voluminous circles only for graphic reasons.
The basic requirement for the influence is the availability of free and mobile charge carriers, i.e. either electrons or ions (these are atoms with a lack or excess of electrons).
If an electrically conductive body, for example a metal, with its large number of freely moving electrons or an insulating material body with only a few free charge carriers , is brought close to a negative charge, a small part of the electrons is shifted to the side facing away from the charge. A positive excess charge then remains on the side facing the charge.
This shift of charge carriers, i.e. electrons or ions, due to the action of an electric field is called influence.
Model presentation
To illustrate this, a conductive (metallic) cuboid is shown in the picture, which comes into an electric field whose field lines are oriented from left to right . This field provides by induction that the electrons move very quickly to the left, because they are attracted to the positive terminal there. The positive ions, which represent the material of the cuboid, remain fixed in their place.
The new distribution of electrons in turn creates an electric field, which is oriented from right to left (red arrows). Inside the cuboid - regardless of whether it is hollow or not - both fields compensate each other and therefore electron migration ends. But if the external field is strengthened, more electrons begin to migrate to the left. Until the increase in the external field inside the cuboid is fully compensated for again. If the polarity of the external field is reversed, the electrons move to the right and all signs are reversed.
At extremely high frequencies, the electrons cannot follow the change in the external field sufficiently quickly, which is why the shielding effect inside the cuboid then decreases ( plasma oscillation ).
This redistribution of electrons also works for any other shape and always has the same effect: The interior of a closed, conductive body is always free of electric field lines at sufficiently low frequencies. The areal charge density on the surface can, however, be very different from place to place.
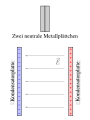
If the conductive body in the field is now cut roughly in the middle across the field, the charges remain separated. The left part of the body is negatively charged and remains so even after removing or switching off the external field. The right part positively charged - there is a potential difference between the parts. If they are separated, one needs energy that comes from the mechanical work of separating them from one another, but not from the energy of the external (influencing) field. This process, carried out as an experiment with two metal plates in the field of an air condenser, is a basic experiment to demonstrate the influence.
- Measurement of the charge displacement due to influence
Influence in isolators
In contrast to electrical conductors, insulating bodies can only be charged electrically poorly because there are only a few freely movable charge carriers.
In the case of metals, the charge transport is limited to the forwarding of the displacement current at the moment of the field change on approach. In the case of insulating bodies, however, polarization occurs , which means that an electric field is also formed along the surface and inside. This leads to an uneven distribution of the charge carriers on the surface of the body. On the side facing away from the field, their polarity corresponds to that of the influencing charge. On the facing side it is of opposite polarity to the influencing charge.
In electrical conductors, the charge carriers move faster than on the surface or even inside bodies of insulating material, because electrons can move freely in the conductor to transport the charge. On and in an insulator, in addition to polarization, the complete shift (current flow) of charge carriers takes place only to a small extent, since there are only very few charge carriers at faults from which they can be detached by a field. The process takes longer because there are fewer freely moving electrons or ions take over the charge transport.
Polarization can cause electrical fields to build up along the surface and inside of insulators , which have a higher energy content than in empty space:
Displacement polarization
The electrical influence does not act on an insulator in the form of a separation of electrical charges by shifting electrons, but by means of the shift polarization . The positive atomic nucleus is pulled in one direction, the oppositely charged electron shell in the other. The electron shell is not deformed! If an alternating field is applied, the positive atomic nucleus “oscillates” back and forth within the negative electron shell. No thermal energy is generated .
Orientation polarization
Influence acts on an electric dipole through orientation polarization . The dipole molecules are aligned with the electric field and thus polarized.
Force effect through influence
The charge separation always causes the influenced body to become an electric dipole . The distance between the centers of gravity of the dissimilar charges is always smaller than the distance between the charges of the same type. It follows from Coulomb's law that the attractive force is always greater than the repulsive force. The difference (net force) is therefore attractive. In practice, the charges that can be achieved are relatively low, so this force of attraction is only noticeable in the case of very low-mass objects such as shredded paper.
In the case of the capacitance diode , influence causes the space charge zone to vary in width .
Demarcation
The effect of influence must be distinguished from contact electricity , e.g. B. the static electricity . With static electricity, charges pass between two bodies in contact. In the case of influence, on the other hand, there is no charge transport between the two bodies involved.
In connection with a variable capacitor, influence can reduce or even increase the electrical voltage without initially generating usable electrical energy. If the bodies involved are separated from each other, they can assume a very high electrical potential. This can lead to undesired arcing . Similar to a charged plate capacitor, the plates of which are removed from each other, the voltage increases because the capacitance C decreases if the charge Q remains the same . This increases the mutual voltage U between the two bodies:
With
- U - potential difference compared to the influencing charge
- Q - constant charge on the body
- C - capacity of the body in relation to the influencing field source or earth
This plays a role in all electrostatic generators , i.e. in the electrophoresis , influenza machines and their further developments Pelletron and Laddertron, but also in the belt generator .
discovery
In 1754 John Canton discovered the change in the distribution of electrical charges on bodies of different materials when they approached them and explained this effect in 1758 at the same time as Johan Carl Wilcke .
Based on Cantons and Wilcke's work, Alessandro Volta constructed the electrophore and the first electroscope in 1775 . He coined the term Influenz.
Historical and current uses
Influence was used in the electrophore to generate electricity inexpensively. In 1787, Abraham Bennet further developed the electrophore to become the so-called Bennet doubler, with which electrostatic voltages can be doubled. In the influence machine , the influence is used in a cycle process for the continuous generation or increase of direct voltage. The Wimshurst machine combines the charge separation through influence with the principle of the Bennet doubler.
In the electroscope , the mechanical forces associated with the influence are used to measure the electrical charge of objects or for currentless voltage measurement.
The Kelvin generator is also based on the effect of the influence.
Pelletrons are used as a DC voltage source in some particle accelerators . They also use Influenz to generate high voltages of up to 32 million volts.
The shielding effect of a Faraday cage against stationary electric fields is also based on the influence.
literature
- Karl Küpfmüller , Gerhard Kohn: Theoretical electrical engineering and electronics. An introduction . 14th improved edition. Springer, Berlin et al. 1993, ISBN 3-540-56500-0 ( Springer textbook ).