Electric field

The electric field is a physical field that acts on electric charges through the Coulomb force . As a vector field , it describes the strength and direction of this force for each point in space via the spatial distribution of the electrical field strength. Electric fields are caused by electric charges and by changes in magnetic fields over time . The properties of the electric field are described together with those of the magnetic field by the Maxwell equations .
The electric field is a ubiquitous phenomenon. It explains, for example, the transmission of electrical energy and the function of electronic circuits. It causes electrons to bind to the atomic nucleus and thus influences the shape of matter . Its combination with magnetism , the electromagnetic field , explains the propagation of light and radio waves.
Description as a vector field
The electric field can be described by the vector field of the electric field strength .
- The vector field of the electric field strength assigns the position and time-dependent vector of the electric field strength to each point in space . The electric field strength describes the force effect on charges and can be determined experimentally by this force effect. If the force acts on an electrical test charge at a location in the absence of a magnetic field , then the electrical field strength is defined by:
- .
- The field emanating from the test charge itself and other forces such as gravity are neglected .
- The vector field of the electrical flux density assigns the location and time-dependent vector of the electrical flux density to each point in space . The electrical flux density can only be measured indirectly. Two properties of the electrical flux density can be used:
- 1. The area integral of the electrical flux density over a closed area (e.g. a spherical surface) is, according to Gaussian law , the same size as the charge contained in the enclosed volume.
- Gaussian law applies regardless of time. Accordingly, it is associated with the idea that the electrical source field caused by charges is already present in the entire room and is not only spreading.
- 2. A temporal change in the electrical flux density acts like an electrical current and appears as a displacement current in the expanded Ampère's law .
The energy density of the electric field results from the electric field strength and the electric flux density
- .
The relationship between the electrical field strength and the electrical flux density depends on the medium and is generally non-linear due to the electrical polarization . The electrical polarization in a material is associated with a charge shift and therefore with an energy transport. It is therefore not instantaneous and is therefore also frequency-dependent. For many media one can still find an approximately linear relationship in the form
with the electric field constant and the permittivity number .
In the vacuum with the relationship between two fields strictly linear, and: .
Field line images
A clear idea of electric fields can be obtained from field line images . These consist of oriented field lines (marked with arrows) . The following applies:
- The field lines of an electric field generated by charges start at positive charges (or at infinity) and end at negative charges (or at infinity). Such a field is called a source field .
- Changes in the magnetic flux passing through a surface create an electrical vortex field . In this case, all electrical field lines are closed.
The direction of the tangent at a point on a field line indicates the direction of the field strength vector at this point, and thus the direction of the force on a positive test charge. The density (the transverse distance) of the field lines is proportional to the magnitude of the field strength at this point.
Examples of electric fields
Electric field of a point charge
The electric field of a point charge is particularly easy to determine. According to Coulomb's law , the field strength at a given point is:
Here stands for the field generating charge at the origin of the coordinate system, for the position vector of the given point, for the associated unit vector , for the electric field constant and for the relative permittivity.
Electric field of any charge distribution
If the electric field is generated by several point charges at the positions , the field strength vector of the total field at the position is obtained according to the superposition principle by adding the individual field strength vectors:
If there is a continuous charge distribution given by the spatial charge density , the following applies accordingly:
Electric field of a line charge
The electric field of a line charge (an infinitely long, charged wire) with the linear charge density is given by
- .
The basis vector is directed radially from the line charge to the reference point.
Electric field of a surface charge
A surface charge (a uniformly charged, infinitely extended, thin plate) creates a homogeneous electric field on both sides . The field strength vector is perpendicular to the plate for any point and away from the plate with a positive charge and towards the plate with a negative charge. Assuming the surface charge density , the electric field strength has the amount
- .
Homogeneous electric field (plate capacitor)
The electric field between two large plane-parallel capacitor plates that contain charges of the same amount but different signs is approximately homogeneous (strictly homogeneous if the plates are infinitely large). The following applies to the amount of field strength:
This is the distance between the plates, the area of a capacitor plate, the voltage between the two plates and the amount of charge on a plate. The potential changes linearly from one plate to the other by the amount . If the plates are moved apart, the field strength remains constant and the voltage increases. The work done against the electrostatic attraction is in the energy of the field . Outside the capacitor, the field strength is (ideally) 0.
The charges on the capacitor plates are evenly distributed over the facing plate surfaces. The absolute amounts of surface charge density
and the electrical flux density match. However, it is a scalar quantity, whereas it is a vector.
If the capacitor is not connected to an external charge source, the value of the surface charge density does not change if a dielectric is inserted or removed from the capacitor plates. However, the electric field strength changes by the factor when added and by the factor when removed .
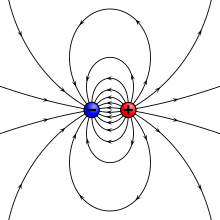
Electric field of a dipole
An electric dipole , an arrangement of two point charges and at a distance , creates a rotationally symmetrical field. For the field strength components parallel and perpendicular to the dipole axis the following applies at a large distance in direction ϑ :
Here, ϑ = 0 points from the center in the direction of the positive charge.
Exactly the formula applies in the limit crossing for vanishing with constant magnitude of the dipole moment .
Conductor in the electric field
If you slowly bring a conductor into an external field that is constant over time, it causes a charge shift ( influence ) in the conductor . The inside remains free of space charges, while a charge distribution is established on the surface that keeps the inside of the conductor free of fields. Outside the field lines are always and everywhere perpendicular to the conductor surface, otherwise the transverse component would cause a further charge shift. High field strengths arise at the tips.
Link with the magnetic field
The electric field in general terms is both location- and time-dependent . It is closely linked to the magnetic field via the Maxwell equations and the special theory of relativity . In the special theory of relativity, its vector components are therefore inseparably combined with those of the magnetic field to form a tensor . Depending on the frame of reference in which one is as an observer, i. H. In which relative movement to any space charges that may be present, the electric field is transformed into a magnetic field and vice versa via the Lorentz transformation .
Difference between electrostatics and electrodynamics
In electrostatics , only static charges are considered. Without currents there is no magnetic field. The electrostatic field is therefore not only stationary , i.e. unchangeable over time, but also rotation-free (eddy-free). Such a field can be described by a potential .
In electrodynamics , on the other hand, one must also take into account electrical fields that are caused by time-varying magnetic fields ( electromagnetic induction ). Electromagnetic waves such as light , which consist of interlinked electrical and magnetic fields, are particularly important . Due to the close relationship between electric and magnetic fields, both are combined in electrodynamics to form the electromagnetic field .
Action at close range instead of action from a distance
Until Heinrich Hertz verified electromagnetic waves , the question was whether the forces acting between electrical charges come about directly in the sense of a long-distance effect or through the mediation of space (close-up effect).
- Coulomb's law is typical of a theory of action at a distance : The essential elements of the arrangement, the charges, appear (in addition to the required information on geometry) both in the equations for the force and in the equations for the energy. Charges in two different places interact from a distance; there is no talk of mediation through space. In the theory of action at a distance, the electric field is only a subordinate calculation variable.
- In a close-up theory, on the other hand, there are only relationships between quantities that are simultaneously present in the same place. The Maxwell equations are an example of a close-range theory. According to these ideas, the fields are of the greatest importance in electrical phenomena. The electrical energy is not considered to be attached to the charges and conductors, but is located in the insulators and in a vacuum and can be transported through them.
As long as only slow changes of the electrical and magnetic quantities are considered, it is not decisive whether one connects one or the other idea with the physical phenomena. However, if one takes into account that impulses and energy can propagate in space with electromagnetic waves, it is difficult to reconcile the idea of an effect at a distance with the observations.
In summary, it is assumed from today's perspective that the interaction between the charges is first mediated by the electric field . Since the force depends on the electric field at the relevant point, but not directly on the electric field at other points, it is a close-up effect. If the position of one of the charges changes, the change in the field spreads through space at the speed of light . A relativistic view of the electric field leads to the electromagnetic field. This can absorb and transport momentum and energy and is therefore just as real as a particle.
Quantization of the electric field
In the context of quantum mechanics , the fields are usually still regarded as classic, even if the states of the interacting particles are quantized . Quantum field theories combine principles of classical field theories (e.g. electrodynamics) and describe particles and fields in a uniform way. Not only observables (i.e. observable quantities) such as energy or momentum are quantized, but also the interacting (particle) fields themselves; the fields are treated similarly to observables. The quantization of the fields is also known as the second quantization .
Individual evidence
- ↑ FK Kneubühl: Repetitorium der Physik, Teubner Study Books Physics. ISBN 3-519-43012-6 , ( limited preview in Google Book Search).
literature
- Adolf J. Schwab: Conceptual world of field theory: practical, clear introduction. Electromagnetic fields, Maxwell's equations, gradient, rotation, divergence . 6th edition. Springer, Berlin 2002, ISBN 3-540-42018-5 .
Web links
- ETH Zurich: Fields at high voltage lines - Animated representation